1前言
交流凈化電源和晶閘管調(diào)感交流穩(wěn)壓電源是一種應(yīng)用廣泛的交流穩(wěn)壓電源,。這種電源的核心是等效電感的計算,。等效電感的構(gòu)成方式有多種,其中常用的是晶閘管調(diào)感式(TCR),,它是通過調(diào)節(jié)晶閘管的控制角α(亦稱觸發(fā)角)來調(diào)節(jié)等效電感Le的大小,。其優(yōu)點(diǎn)是簡單,造價低,,缺點(diǎn)是產(chǎn)生的諧波較大,,使電感損耗增加,對市電污染也較大;另一種是具有發(fā)展前途的高頻PWM斬波器調(diào)感式(PCR),,這種電路是通過調(diào)節(jié)IGBT交流斬波器的脈沖寬度來調(diào)節(jié)等效電感Le的大小,。其優(yōu)點(diǎn)是產(chǎn)生的諧波小,,對電感損耗影響不大,,對市電污染也比較小,缺點(diǎn)是使用元器件多,,造價高,。
在設(shè)計凈化電源或晶閘管調(diào)感交流穩(wěn)壓電源時,必須對等效電感Le進(jìn)行計算,。目前,,晶閘管調(diào)感式電路Le的計算方法有三種,它們的正確性和內(nèi)在關(guān)系是本文研究的重要內(nèi)容之一,,本文研究的另一重要內(nèi)容是介紹高頻PWM斬波器調(diào)感電路(PCR)的應(yīng)用,。
2晶閘管調(diào)感電路Le的計算
晶閘管調(diào)感電路Le的計算式有兩種求法:即電感電流法和電感電壓法。
21用電感電流求Le當(dāng)用晶閘管調(diào)感時,,晶閘管的導(dǎo)通角θ與控制角α和電感功率因數(shù)角φ有關(guān),。當(dāng)控制角α>φ時電感電壓和電流的波形如圖1所示。流過電感L的電流有兩個分量,,即穩(wěn)定分量i1和自由分量i2:
i1![]() =sin(ωt+α-φ)
=sin(ωt+α-φ)
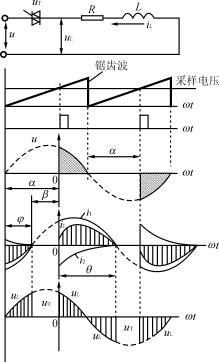
圖1感性負(fù)載α>φ時的波形圖

圖2α>φ時θ與α和φ的關(guān)系曲線
![]() 圖3φ≤時等效電路與波形圖
圖3φ≤時等效電路與波形圖
i2![]()
![]() =-sin(α-φ)
=-sin(α-φ)
iL=i1+i2![]() =〔sin(ωt+α-φ)-
=〔sin(ωt+α-φ)-![]() sin(α-φ)〕(1)
sin(α-φ)〕(1)![]() 式中:Z=,;
式中:Z=,;![]() φ=tg-1;
φ=tg-1;
R為電感L的繞組電阻,。
導(dǎo)通角θ與控制角α和電感的功率因數(shù)角φ的關(guān)系曲線如圖2所示,。
由式(1),當(dāng)忽略電感電阻令R=0,α-φ=β(見圖1)則得:
iL![]() =〔sin(ωt+α-φ)-sin(α-φ)〕
=〔sin(ωt+α-φ)-sin(α-φ)〕![]() =〔sin(ωt+β)-sinβ〕(2)
=〔sin(ωt+β)-sinβ〕(2)
iL是奇諧波函數(shù),,將iL用付里葉級數(shù)表示時可以將iL分成基波iL1和諧波iLn兩部分表示:
iL![]()
![]() 1=(3)
1=(3)
iL![]() n={
n={![]() ·sinnωt},(k=1,2,3…)(4)
·sinnωt},(k=1,2,3…)(4)![]() 由方程(3)的基波電流方程式可知,,如果令其中的,則等效電感Le的計算式為:
由方程(3)的基波電流方程式可知,,如果令其中的,則等效電感Le的計算式為:![]() Le=(5)
Le=(5)
22用電感電壓求Le
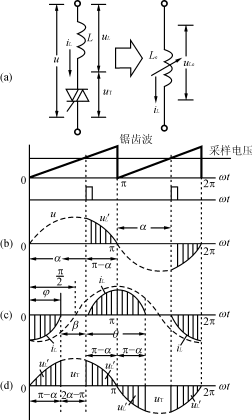
忽略電感中的電阻,,晶閘管調(diào)感的電路和波形如圖3所示,,其中圖3(a)為電路和等效電路,如圖3(b)為外施電壓u的受控波形,,圖3(c)為電流iL的的波形,,圖3(d)為電感L上承受的電壓波形。在圖3中:u為外施電壓,、uL為電感上電壓,、uT為晶閘管上電壓。當(dāng)晶閘管導(dǎo)通時,,uT=0,,uL=u;當(dāng)晶閘管關(guān)斷時,uT=u,,uL![]()
![]() =0,。即只有在晶閘管導(dǎo)通時的θ區(qū)間內(nèi),電感L上才有電壓,。由于電感L的作用,,使電流滯后于電壓u為φ=角。當(dāng)晶閘管的控制角為α>φ時,,晶閘管的導(dǎo)通角為θ,,由圖2所示的θ與α和φ的關(guān)系曲線可知,當(dāng)φ=時θ與α之間的關(guān)系為:
=0,。即只有在晶閘管導(dǎo)通時的θ區(qū)間內(nèi),電感L上才有電壓,。由于電感L的作用,,使電流滯后于電壓u為φ=角。當(dāng)晶閘管的控制角為α>φ時,,晶閘管的導(dǎo)通角為θ,,由圖2所示的θ與α和φ的關(guān)系曲線可知,當(dāng)φ=時θ與α之間的關(guān)系為:![]() θ=π·=2(π-α)(6)
θ=π·=2(π-α)(6)![]() 由圖3(b),、圖3(c),,可以看出,當(dāng)φ=時,,電流iL的導(dǎo)通角θ被ωt=0,、π、2π…的縱軸線平分,,縱軸線兩邊iL導(dǎo)通的寬度各為(π-α),,正好與圖3(b),u導(dǎo)通的區(qū)間(π-α)相等,。由于θ=2(π-α),,所以就使圖3(d)所示電感上電壓增大了一倍,即在晶閘管導(dǎo)通的θ區(qū)間內(nèi),,uLe=2uL′,。
由圖3(b),、圖3(c),,可以看出,當(dāng)φ=時,,電流iL的導(dǎo)通角θ被ωt=0,、π、2π…的縱軸線平分,,縱軸線兩邊iL導(dǎo)通的寬度各為(π-α),,正好與圖3(b),u導(dǎo)通的區(qū)間(π-α)相等,。由于θ=2(π-α),,所以就使圖3(d)所示電感上電壓增大了一倍,即在晶閘管導(dǎo)通的θ區(qū)間內(nèi),,uLe=2uL′,。
由圖3(d)可知,加在電感Le上的電壓方程式應(yīng)為: 由于圖3(d)是鏡對稱的奇函數(shù),,所以只須對半個周期積分就可以求出uLe的基波與各次諧波幅值,。同時uLe的付立葉級數(shù)中將不包含恒定分量及偶
由于圖3(d)是鏡對稱的奇函數(shù),,所以只須對半個周期積分就可以求出uLe的基波與各次諧波幅值,。同時uLe的付立葉級數(shù)中將不包含恒定分量及偶
次諧波。![]() uLe=(ancoonωt+bnsinnωt)(8)
uLe=(ancoonωt+bnsinnωt)(8)
式中:ao=0![]() an=
an=![]()
![]() (9)
(9)![]() bn=
bn=![]()
![]()
![]() =2(10)
=2(10)
對于基波,,n=1,,a1=0![]() b1=
b1=![]()
![]()
![]() =(π-α+sin2α)(11)
=(π-α+sin2α)(11)
所以uLe=b1sinωt![]()
![]() =2(π-α+sin2α)sinωt(12)
=2(π-α+sin2α)sinωt(12)
加在晶閘管調(diào)感電路電感上的電壓為:
uL=ULmsinωt(13)
式(12)與式(13)相等,當(dāng)用有效值表示時,,兩邊各除以電流有效值IL則得:![]()
![]()
![]() (π-α+sin2α)
(π-α+sin2α)![]()
![]() ωL=(π-α+sin2α)ωLe
ωL=(π-α+sin2α)ωLe![]()
![]() Le=,,
Le=,,![]() (≤α≤π)(14)
(≤α≤π)(14)
文獻(xiàn)(2)的計算結(jié)果為:![]()
![]() Le′=,(≤α≤π)(15)
Le′=,(≤α≤π)(15)
此式計算有兩個錯誤:一是不應(yīng)該用圖3(b)的波形而應(yīng)該用圖3(d)的波形,;二是圖3(b)是鏡對稱,,an≠0,a1≠0,,所以文獻(xiàn)2對式(15)的推導(dǎo)是錯的,,但可以用,。
23三種等效電感計算式之間的關(guān)系
式(5)、式(14),、式(15)三種計算等效電感方程式之間的關(guān)系是:
式(14)表示的是Le與控制角α之間的關(guān)系,,使用比較方便,故應(yīng)用較普遍,,式(5)在介紹穩(wěn)壓原理時使用方便,,這兩公式形式不同但實質(zhì)是一樣的。式(15)是不正確的,,但可以用,,在應(yīng)用時必須要除2才能得到正確值,。
3高頻PWM斬波器調(diào)感電路Le的計算![]() 高頻PWM斬波器調(diào)感的等效電路如圖4所示,,斬波開關(guān)用IGBT和一個單相整流橋組成,由于工作于高頻,,所以采用了軟開通和軟關(guān)斷緩沖電路,,以減小IGBT的開關(guān)損耗。開關(guān)控制采用了EPWM直流等電位調(diào)制技術(shù),。觸發(fā)脈沖的形成與交流電壓PWM斬波波形如圖5所示,。為使波形半波奇對稱和四分之一偶對稱,以消除付里葉級數(shù)中的余弦項和偶次諧波,,使載波比N==4K,,K=1,2,3…,fc
高頻PWM斬波器調(diào)感的等效電路如圖4所示,,斬波開關(guān)用IGBT和一個單相整流橋組成,由于工作于高頻,,所以采用了軟開通和軟關(guān)斷緩沖電路,,以減小IGBT的開關(guān)損耗。開關(guān)控制采用了EPWM直流等電位調(diào)制技術(shù),。觸發(fā)脈沖的形成與交流電壓PWM斬波波形如圖5所示,。為使波形半波奇對稱和四分之一偶對稱,以消除付里葉級數(shù)中的余弦項和偶次諧波,,使載波比N==4K,,K=1,2,3…,fc![]()
![]()
![]()
![]()
![]()
![]()

圖4用高頻PWM斬波器調(diào)感的等效電路
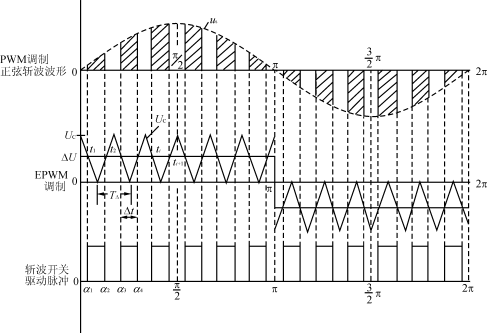
圖5EPWM調(diào)制與正弦PWM斬波波形
![]()
![]() 為三角波頻率,,fs為市電工頻,;調(diào)制M=,Δt為脈沖寬度,,TΔ=為三角波周期,、Uc為三角波幅值、ΔU為輸出電壓的偏差,、三角波電壓的方程式為:
為三角波頻率,,fs為市電工頻,;調(diào)制M=,Δt為脈沖寬度,,TΔ=為三角波周期,、Uc為三角波幅值、ΔU為輸出電壓的偏差,、三角波電壓的方程式為: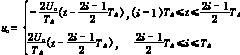
i=1,2,3…(16)
輸出電壓偏差ΔU為采樣電壓,,觸發(fā)脈沖起點(diǎn)ti和終點(diǎn)ti+1的方程式為:![]()
![]()
![]() 脈沖寬度Δt=
脈沖寬度Δt=![]() 式中TΔ=,各觸發(fā)脈沖的起點(diǎn)角和終點(diǎn)角的數(shù)值為:
式中TΔ=,各觸發(fā)脈沖的起點(diǎn)角和終點(diǎn)角的數(shù)值為:![]()
![]() α1=(1-M);α2=(1+M)
α1=(1-M);α2=(1+M)![]()
![]() α3=(3-M);α4=(3+M)
α3=(3-M);α4=(3+M)
由于PWM斬波波形是鏡對稱和原點(diǎn)對稱,,因此它的付里葉級數(shù)中將只包含正弦項中的奇次諧波,,即:![]() uL=bnsinnωtn為奇數(shù)
uL=bnsinnωtn為奇數(shù)![]()
![]() bn=uLsinnωtd(ωt)=sinωt·sinnωtd(ωt)
bn=uLsinnωtd(ωt)=sinωt·sinnωtd(ωt)![]() +sinωt·sinnωtd(ωt)+…)(17)
+sinωt·sinnωtd(ωt)+…)(17)
經(jīng)計算,當(dāng)n=KN±1時(K=1,,2,,3…)![]() bn=KN±1=sinωt·sinnωtd(ωt)
bn=KN±1=sinωt·sinnωtd(ωt)![]() =-(18)
=-(18)
當(dāng)n≠KN±1時,bn≠KN±1=0
對于基波,,n=1![]()
![]() b1=sin2ωtd(ωt)+sin2ωtd(ωt)+…)
b1=sin2ωtd(ωt)+sin2ωtd(ωt)+…)![]()
![]()
![]() =sin2ωtd(ωt)=
=sin2ωtd(ωt)=
=MUm(19)
uLe=MUmsinωt![]()
![]() -sinKMπ·
-sinKMπ·
sin(KN±1)ωt(20)![]() 由式(18)的諧波幅值sinKMπ可以算出:當(dāng)fc=10kHz,,N=200,,M=0.1~0.9時,基波和各次諧波幅值與Um之比如表1所示,,它們和調(diào)制比M的關(guān)系曲線如圖6所示,。可知,,N越大諧波頻率越高,。當(dāng)fc=50kHz,N=1000時用電路中L1=50mH,,C=0.1μF就可以濾掉uLe中的所有高次諧波,。
由式(18)的諧波幅值sinKMπ可以算出:當(dāng)fc=10kHz,,N=200,,M=0.1~0.9時,基波和各次諧波幅值與Um之比如表1所示,,它們和調(diào)制比M的關(guān)系曲線如圖6所示,。可知,,N越大諧波頻率越高,。當(dāng)fc=50kHz,N=1000時用電路中L1=50mH,,C=0.1μF就可以濾掉uLe中的所有高次諧波,。
如求等效電感Le,由圖4
表1基波和各次諧波幅值與Um之比(fc=10kHz,N=200)
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
|---|---|---|---|---|---|---|---|---|---|
| b1/Um | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| b199/Um | -0.0984 | -0.1871 | -0.2575 | -0.3027 | -0.3183 | -0.3027 | -0.2575 | -0.1871 | -0.0984 |
| b201/Um | -0.0984 | -0.1871 | -0.2575 | -0.3027 | -0.3183 | -0.3027 | -0.2575 | -0.1871 | -0.0984 |
| b399/Um | -0.0935 | -0.1514 | -0.1514 | -0.0935 | 0 | 0.0935 | 0.1514 | 0.1514 | 0.0935 |
| b401/Um | -0.0935 | -0.1514 | -0.1514 | -0.0935 | 0 | 0.0935 | 0.1514 | 0.1514 | 0.0935 |
| b599/Um | -0.0858 | -0.1009 | -0.0328 | 0.0624 | 0.1061 | 0.0624 | -0.0328 | -0.1009 | -0.0858 |
| b601/Um | -0.0858 | -0.1009 | -0.0328 | 0.0624 | 0.1061 | 0.0624 | -0.0328 | -0.1009 | -0.0858 |
| b799/Um | -0.0757 | -0.0468 | 0.0468 | 0.0757 | 0 | -0.0757 | -0.0468 | 0.0468 | 0.0757 |
| b801/Um | -0.0757 | -0.0468 | 0.0468 | 0.0757 | 0 | -0.0757 | -0.0468 | 0.0468 | 0.0757 |
M
諧波分量
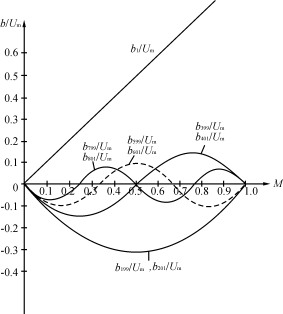
圖6諧波分量與調(diào)制比M的關(guān)系曲線
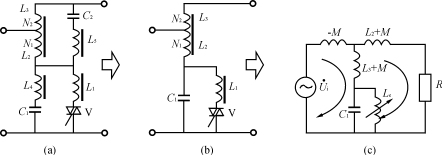
圖7穩(wěn)壓電源主電路及其等效電路
(a)主電路(b)簡化電路(c)等效電路
可知需使uL=uLe,,uL=ULmsinωt,,對于uLe忽略掉其中的高次諧波時(高次諧波被L、C濾掉)uLe=MUm·sinωt,,當(dāng)uL,、uLe用有效值表示時:UL=MULe,兩邊各除以電流iL的有效值IL,,則可得:![]() ωL1=MωLe,,Le=(21)
ωL1=MωLe,,Le=(21)
4穩(wěn)壓電源的輸出電壓方程式
交流凈化電源和晶閘管調(diào)感式交流穩(wěn)壓電源的主電路和等效電路如圖7所示,其中L1,、L4,、L5為線性電感。L4,、C1組成三次諧波濾波電路,,L5、C2組成五次諧波濾波電路,,雙向晶閘管V和L1組成調(diào)感支路,,圖7(a)為主電路,圖7(b)為簡化電路,,圖7(c)為等效電路,。
對圖7(c)用基爾霍夫定律可得到如下方程:![]()
![]() =〔-jωM+jω(L2+M)+jωLX〕-
=〔-jωM+jω(L2+M)+jωLX〕-![]() 〔jω(L2+M)+jωLX〕
〔jω(L2+M)+jωLX〕![]()
![]() =〔jω(L2+M)+jωLX〕-
=〔jω(L2+M)+jωLX〕-![]() 〔jω(L3+M)+jω(L2+M)+jωLX〕
〔jω(L3+M)+jω(L2+M)+jωLX〕![]() 兩式聯(lián)立對求解得:
兩式聯(lián)立對求解得:![]()
![]()
![]()
![]() 式中M=;LX=,;=R
式中M=;LX=,;=R
由式(22),,在已知L1、L2,、L3,、C1、R和uo的條件下,,當(dāng)輸入電壓ui發(fā)生變化時,,通過調(diào)節(jié)LX(實際上就是調(diào)節(jié)等效電感Le)就可以使輸出電壓uo保持穩(wěn)定,。
5實驗結(jié)果
對3kVA交流凈化電源進(jìn)行實驗,L1=60mH,,L2=193mH,,L3=21.4mH,C=20μF,,R=16.1Ω,,
![]() (22)
(22)
10Mbps,還是100Mbps,?
在這里要跟各位介紹以太(Ethernet)局域網(wǎng)的實際成品發(fā)展,,也就是美國國家半導(dǎo)體(NationalSemiconductor)的1Gbps的以太網(wǎng)芯片,這是針對網(wǎng)卡(NICs,NetworkInterfaceCards)用的芯片,,而非網(wǎng)絡(luò)集線器(Hub)或網(wǎng)絡(luò)交換機(jī)(Switch)用的芯片,。雖然這套芯片在2000年5月已經(jīng)正式推出,但真正生產(chǎn)則是在去年下半年,,至于真正的普及與起飛則得看今年了,。
1Gbps的以太網(wǎng)若很單純地想,,應(yīng)該就是比現(xiàn)有100Mbps快10倍而已,,如果各位只是這樣想,可真的有點(diǎn)小看1Gbps的以太網(wǎng)嘍,!
UO=220V,,通過Le計算式和式(22)聯(lián)合進(jìn)行計算,并用示波器實測α值證明,,控制角的計算值與實測α值之間的偏差≤2°,。
6結(jié)語
本文通過分析得到的等效電感Le的計算式(5)及式(14)是正確的,在用式(15)Le′的計算式計算等效電感時必須要除2才能得到正確結(jié)果,。
晶閘管調(diào)感法經(jīng)濟(jì),、簡單,但產(chǎn)生的諧波較大,,不僅增加了被控電感的損耗,,也對市電有污染。而高頻PWM斬波器調(diào)感法雖也產(chǎn)生諧波,,但頻率較高,,由被控電感和很小的濾波電容即可濾掉所有高次諧波,被控電感損耗相對較小,,基本對市電無污染,,能滿足嚴(yán)格的諧波規(guī)范要求,是很有前途的一種調(diào)感法,。

