摘  要： 文本聚類在很多領(lǐng)域都有廣泛應(yīng)用,，而聚類算法作為文本聚類的核心直接決定了聚類的效果和效率。結(jié)合基于劃分的聚類算法和基于密度的聚類算法的優(yōu)點(diǎn),，提出了基于密度的聚類算法DBCKNN,。算法利用了k近鄰和離群度等概念,，能夠迅速確定數(shù)據(jù)集中每類的中心及其類半徑，在保證聚類效果的基礎(chǔ)上提高了聚類效率,。
關(guān)鍵詞： 文本聚類,；基于密度；k近鄰,；離群度

    文本聚類是指將n篇文章聚集成k類,，使得每類內(nèi)的樣本相似度較大，每類間的樣本相似度較小,。文本聚類是一種特殊的數(shù)據(jù)聚類,，有著自身的特點(diǎn)。文本的聚類對象維數(shù)較高,，決定了聚類算法需要快速收斂,，注重效率。國內(nèi)外也圍繞著文本聚類提出了很多理論和算法,，采用的核心聚類算法一般分為兩類,，一類是基于劃分的聚類算法，如K-means算法,、CLARANS算法等,；另一類是基于密度的聚類算法，如KNNCLUST算法,、DBSCAN算法等,。
1 基于密度聚類算法的研究與改進(jìn)
1.1現(xiàn)有算法的缺陷
    K-means算法與DBSCAN算法分別作為基于劃分和基于密度的聚類算法的代表，被廣泛應(yīng)用于文本聚類中,。其中K-means算法有實(shí)現(xiàn)簡單,、時間復(fù)雜度低等優(yōu)點(diǎn)，但算法需要指定種類數(shù),，且對初始點(diǎn)依賴性過強(qiáng),，導(dǎo)致聚類效果不理想；DBSCAN算法則有抗噪音性強(qiáng),、聚類準(zhǔn)確性高等優(yōu)點(diǎn)，但算法的主要閾值參數(shù)很難確定,，且時間復(fù)雜度過高,，導(dǎo)致聚類效果不理想。
    本文將K-means算法的特性,，融入到利用k近鄰概念的基于密度的聚類算法中,，提出了DBCKNN算法(Density-Based Clustering using K-Nearest Neighbor)，在保證算法準(zhǔn)確性的前提下,，提高了算法效率,。


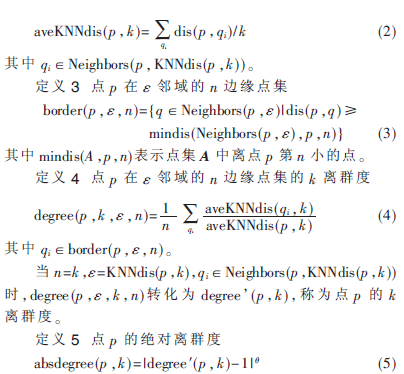
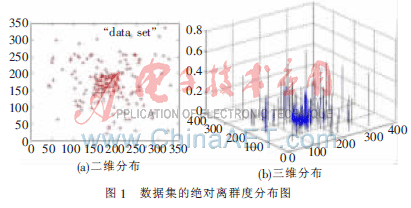
點(diǎn)的絕對離群度域值為(0,，+∞)，且值越小,，表示點(diǎn)越有可能為類中點(diǎn),，反之，表示點(diǎn)越有可能為噪音點(diǎn),。θ一般取不大于3的正整數(shù),，θ越大，不同對象的絕對離群度分布越離散,。如圖1(a)中類近似為高斯分布,，圖1(b)中z軸為點(diǎn)的絕對離群度值，其θ取1,?？梢钥闯觯绞穷愔行牡狞c(diǎn),，其絕對離群度越小,，而類邊緣和噪音點(diǎn)都有相對高的絕對離群度值。

    定義6 邊緣點(diǎn)集的k平均近鄰距離的均值

1.3 算法改進(jìn)
1.3.1 確定類初始中心核心子算法FINDCENTER(ε)
    現(xiàn)有的基于密度的聚類算法中,，通常會對全體點(diǎn)進(jìn)行一次密度值掃描,，導(dǎo)致算法復(fù)雜性和空間復(fù)雜性過高。改進(jìn)后的算法,，利用劃分算法中迭代并更新中心點(diǎn)的思想,，可以對定半徑的超球體的移動具有指導(dǎo)性，使得落入超球體內(nèi)部的點(diǎn)相對更多,，即超球體的密度相對更大,。
    算法1 FINDCENTER(ε)
    算法輸入：p，ε,；算法輸出：p
    (1)以ε為鄰域半徑,，求|Neighbors(p，ε)|和absdegree(p,，k),。
   
    算法中的λ取值一般為0~1。λ取值越小,，半徑變化越小,，迭代次數(shù)越多，但最終得到類半徑的值越準(zhǔn)確,。算法中的(α,，β)域越寬，聚類粒度越大。算法中的n是不大于k的正整數(shù),，一般取值和k相同,。n取值越大，則時間復(fù)雜度越高,，但最終得到類半徑的值越準(zhǔn)確,。
1.3.3 DBSCAN算法思想
    在數(shù)據(jù)對象集中找到absdegree(p，k)大于閾值的對象p后,，通過反復(fù)迭代FINDCENTER(ε)和ADJUSTRADIUS(p,，ε)，找出初始類Ci,，并將Ci排除出數(shù)據(jù)對象集,。重復(fù)上述過程，生成初始類集,。通過初始類集中各類間的包含關(guān)系和評價函數(shù),，將噪音點(diǎn)集從初始類集中提取出。最后將噪音點(diǎn)集中的對象按與類集中各類中心點(diǎn)的距離分配給各個類,。
2 實(shí)驗(yàn)
    通過實(shí)驗(yàn)對DBCKNN算法的聚類效果和時間效率進(jìn)行對比和分析,。數(shù)據(jù)集采用兩個著名的數(shù)據(jù)集Iris和KDDCUP1000。測試數(shù)據(jù)集信息如表1,。這兩個數(shù)據(jù)集每一類的數(shù)據(jù)映射到高維空間中近似為正凸型的超球體,，符合文本聚類中所提取的文本特征向量的分布情況，其中Iris為3類,，KDDCUP1000為5類,。實(shí)驗(yàn)用VC6.0編寫，在配置PentiumⅣ 2.4 GB CPU,、內(nèi)存1 GB,、80 GB硬盤的計(jì)算機(jī)上運(yùn)行。

    本文對聚類效果的評判標(biāo)準(zhǔn)采用參考文獻(xiàn)[4]中提出的聚類質(zhì)量判定式：S-Dbw(c)=Scat(c)+Dens-bw(c),，其中c為類集,，Dens-bw(c)評價的是各類間的平均密度，值越小表示類間區(qū)分度越好,；Scat(c)評價的是類內(nèi)元素的相似性,，值越小表示類越內(nèi)聚。
    對經(jīng)典算法K-means,、DBSCAN和本文提出的DBCKNN算法在聚類效果和效率上做對比,。其中K-means算法的k分別取3和5，并對初始點(diǎn)集做預(yù)處理,，盡量使初始點(diǎn)集分散且局部密度相對大，DBSCAN算法的minpts,、eps取2.5,，DBCKNN算法的λ取0.5,，k、n取20,，θ取2,，(α，β)取(0.9,，1.1),。
    圖2為預(yù)處理后的K-means算法、DBSCAN算法和DBCKNN算法對測試數(shù)據(jù)集的聚類效果比較,。
    從圖2可以看出,，雖然已經(jīng)對初始點(diǎn)集做了預(yù)處理，而且對k取了正確的值,，但是K-means算法效果仍然不理想,。由于DBSCAN算法在數(shù)據(jù)對象密度的處理上更精確，在數(shù)據(jù)對象維數(shù)較低時,，效果略好于DBCKNN算法,；而當(dāng)數(shù)據(jù)對象維數(shù)較高時，高維空間中數(shù)據(jù)分布稀疏,，DBSCAN算法會誤將部分?jǐn)?shù)據(jù)對象視為噪音點(diǎn),，從而對聚類效果產(chǎn)生負(fù)面影響，而由于DBCKNN算法采用k近鄰距離作為密度探測半徑,，對噪音點(diǎn)的處理更加合理,，所以在數(shù)據(jù)對象維數(shù)較高時效果要略好于DBSCAN算法。

    圖3為K-means算法,、DBSCAN算法和DBCKNN算法對測試數(shù)據(jù)集的聚類效率,。

    從圖3可以看出，K-means算法的效率非常高,，在常數(shù)次迭代就得到聚類結(jié)果,，數(shù)據(jù)規(guī)模對聚類效率的影響有限；DBSCAN算法要對所有數(shù)據(jù)對象的密度進(jìn)行一次以上的處理,，聚類效率依賴于數(shù)據(jù)規(guī)模,，導(dǎo)致效率相對低下；本文的DBCKNN算法會根據(jù)數(shù)據(jù)對象局部區(qū)域的密度信息來評價這個局部區(qū)域所有數(shù)據(jù)對象的密度信息,，所以聚類效率比K-means算法低,，但遠(yuǎn)高于DBSCAN算法。
    本文結(jié)合了基于劃分的聚類算法和基于密度的聚類算法各自的優(yōu)點(diǎn),，提出了一種能夠快速找到類中心并自適應(yīng)類半徑的聚類算法DBCKNN算法,。DBCKNN算法能在對高維空間下每類形似正凸形超球體的數(shù)據(jù)對象集進(jìn)行相對準(zhǔn)確的聚類情況下，提高算法效率。另外,，本文通過分析及實(shí)驗(yàn)數(shù)據(jù)對比,，從聚類效果和聚類效率兩方面驗(yàn)證了這種改進(jìn)方法的正確性和高效性。進(jìn)一步將這種方法和基于語義的聚類方法相結(jié)合,，應(yīng)用于聚類搜索引擎等數(shù)據(jù)挖掘領(lǐng)域,，是下一步研究的重點(diǎn)。
參考文獻(xiàn)
[1] 孫吉貴．聚類算法研究[J]．軟件學(xué)報,，2008,，19(1)：48-61．
[2] KANUNGO T， MOUNT D M,， NETANYAHU N,， et al． A local search approximation algorithm for K-means clustering[J]．Computational Geometry， 2004(28)： 89-112．
[3] 汪中．一種優(yōu)化初始中心點(diǎn)的K-means算法[J]．模式識別與人工智能,，2009,，22(2)：300-304．
[4] HALKIDI M， VAZIRGIANNIS M． Clustering validity assessment： finding the optimal partitioning of a data set[C]． In： Proc．of the 1st IEEE Int’I Conf．on Data Mining．187-194．
[5] 談恒貴．?dāng)?shù)據(jù)挖掘中的聚類算法[J]．微型機(jī)與應(yīng)用,，2005(1)．