??? 摘? 要： 在時延和頻移兩個方向上,，對跳頻信號的模糊函數(shù)進(jìn)行了分析,，提出了一種基于跳頻信號模糊函數(shù)自項特征的時頻表示方法。其核函數(shù)在信號的模糊域能夠有效地濾除噪聲和交叉項,，并保留絕大部分的自項能量,。仿真試驗結(jié)果證實,，與平滑偽維格納分布相比較，該方法提高了信號項的時頻聚集性,，具有更好的參數(shù)估計性能,。?

??? 關(guān)鍵詞： 跳頻信號； 核函數(shù),； 參數(shù)估計,； 模糊函數(shù)

?

??? 跳頻信號具有很強(qiáng)的抗干擾和抗截獲能力，一經(jīng)出現(xiàn)便在軍事通信中得到了廣泛的應(yīng)用,。作為典型的非平穩(wěn)信號,，其頻譜隨時間快速變化。傳統(tǒng)的傅立葉分析不能有效描述跳頻信號的頻率變化，而時頻分析從時間和頻率兩個維度上描述了信號的能量變化,，因此,，時頻表示成為跳頻信號分析的有力工具。?

??? 應(yīng)用比較廣泛的時頻分析方法,，是信號的雙線性時頻表示,。為了在保持時頻分辨率的同時，有效抑制交叉項,，眾多的學(xué)者對此展開了深入研究,，產(chǎn)生了類型眾多的時頻表示方法^[1]。由于跳頻信號的非線性調(diào)頻性質(zhì),，其交叉項干擾尤為嚴(yán)重,。平滑類維格納分布SPWVD(Smoothed Pseudo-Wigner Distribution)在時間和頻率兩個方向?qū)π盘柕木S格納分布實現(xiàn)平滑，極大地抑制了交叉項的影響^[2-3],；另外,，SPWVD分布核函數(shù)形狀簡單、與信號時頻結(jié)構(gòu)關(guān)聯(lián)不大,，從而得到了廣泛研究^[4-7],。1997年，Barbaross^[5]首次將維格納分布引入跳頻信號的參數(shù)估計中,，它采用時域平滑的方法抑制交叉項,，并給出了粗略的參數(shù)估計算法。在信噪比大于6dB情況下得到了準(zhǔn)確的跳頻周期,。張朝陽等^[6]提出在時頻域平滑的平滑偽維格納分布來同時抑制時頻兩個方向上的交叉項，可以在信噪比大于4dB時得到跳頻駐留時間和跳頻時刻的有效提取,。參考文獻(xiàn)[7]將重排SPWVD方法應(yīng)用于跳頻信號分析,，實現(xiàn)在0dB時提取信號駐留時間以及跳變時刻。但是,，平滑方法在抑制交叉項的同時,，降低了信號的時頻分辨率，重排算法又使運(yùn)算量急劇增加,，都無法滿足實際應(yīng)用中對跳頻信號參數(shù)估計的需求,。?

??? 本文首先建立跳頻信號模型，然后針對跳頻信號模糊域特征,，提出一種新的時頻分析方法,，并與SPWVD方法做了比較，指出其優(yōu)越性,。?

1 Cohen類二次型時頻表示?

??? 信號x(t)的Cohen類時頻分布統(tǒng)一表示為：?

?????

??? 積分區(qū)間在(-∞,+∞),，其中A(τ,v)是信號的模糊函數(shù)，定義為:?

?????

??? Φ(τ,v)為時頻分布的核函數(shù)，決定著不同的時頻分布及其屬性,。實際應(yīng)用中,，信號屬性差別很大，對時頻特征的要求也不盡相同,，固定核函數(shù)很難滿足信號時頻分析要求^[1],，而自適應(yīng)方法的運(yùn)算量又比較大^[8-9]；客觀上要求針對具體應(yīng)用,，結(jié)合信號分析要求的時頻屬性,，對核函數(shù)進(jìn)行設(shè)計。本文基于跳頻信號模糊平面分析,，結(jié)合參數(shù)估計的具體應(yīng)用,，提出了一種新的時頻表示方法。?

2? 跳頻信號模型及其模糊函數(shù)分析?

2.1 跳頻信號模型

??? 跳頻信號x(t)可以看作一個單音脈沖信號x₀(t)時頻移位的結(jié)果,，即:?

?????

其中,，是寬度為T_H的矩形窗，T_H為跳頻周期,，f_k是跳頻頻率,，αT_H是跳變時刻。?

??? 在本文的分析中,，假設(shè)跳頻信號的參數(shù)與參考文獻(xiàn)[6]類似,。觀測時間為8個跳頻周期，跳頻頻率f_k依次為{5,45,20,10,35,15,25,40,30}Hz,，采樣率為f_s=100Hz,，跳頻周期T_H=0.32s，跳變時刻αT_H=TH/2,。?

2.2 跳頻信號的模糊函數(shù)?

??? 把(3)式代入(2)式中,，得到跳頻信號的模糊函數(shù)表示：?

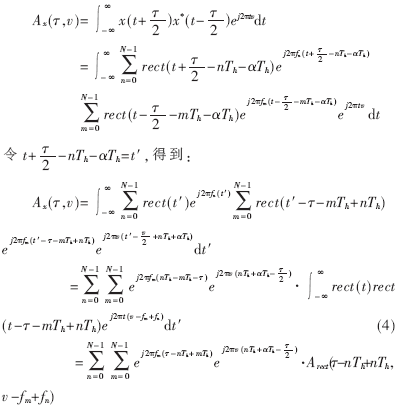
（定義下同）的模糊函數(shù)，即：?

?????

??? 由（4）式可以看出,，隨機(jī)跳頻信號的模糊函數(shù)是由A_rect(τ,v)按照一定規(guī)律經(jīng)過時移,、頻移后加權(quán)疊加而成的，形成平行于τ軸的帶狀結(jié)構(gòu),。在時延方向上模糊帶的中心間隔相同,，為T_h，頻率方向上的間隔由于跳變而呈現(xiàn)一種隨機(jī)性,。?

??? 當(dāng)m=n時,，模糊平面中心附近由N個子脈沖的A_rect函數(shù)疊加而成，構(gòu)成信號的自項部分,，即:?

?????

??? 由此可見,，跳頻信號模糊函數(shù)的自項由子脈沖模糊函數(shù)加權(quán)得到,，在頻移方向上具有抽樣函數(shù)形式。結(jié)合式（5）可知,，其主瓣寬度在原點(diǎn)處具有最小值,，隨著時延的增加（遠(yuǎn)離模糊平面原點(diǎn)）而增加，呈現(xiàn)“啞鈴”狀,，其中主瓣中心窄,，兩端寬，而旁瓣分布在“啞鈴”的兩個側(cè)向,，沿著頻移方向無限延伸,，其等高線見圖1，盡管由于頻率的隨機(jī)性使得等高線不連續(xù),，但是其形狀仍然具有上述特點(diǎn),。?

?

?

3 核函數(shù)設(shè)計?

3.1 核函數(shù)?

??? 由第二節(jié)可知，跳頻信號模糊函數(shù)自項在時延方向上的寬度為跳周期,，頻移方向上表現(xiàn)為抽樣函數(shù)形式,，其主瓣寬度隨著時延的大小而改變。根據(jù)式(1)模糊域的時頻表示可知,，“理想”時頻表示要求信號模糊函數(shù)與核函數(shù)要盡量匹配,，在抑制信號互模糊帶的同時，使自模糊帶盡可能通過,，因此,，提出一種新的時頻核函數(shù)，定義為：?

?????

其中,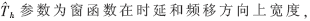c是一常數(shù),，控制著信號自項的擴(kuò)展程度,，取值應(yīng)滿足聚集性和交叉項抑制的要求，一般應(yīng)小于最小跳頻頻率間隔,。?

3.2 參數(shù)設(shè)計?

??? 設(shè)計核函數(shù)的性能與參數(shù)有關(guān),。由式（4）可以看出，跳頻信號模糊平面各帶在頻移方向上的距離等于跳頻頻率間隔,，實際跳頻通信系統(tǒng)中，不僅各個跳頻頻率各不相同,，而且必須滿足一定的頻率間隔,。因此，盡管跳頻頻率具有隨機(jī)性,，但是互模糊帶不可能位于時延軸上,，距離時延軸的最小距離由跳頻頻率的最小間隔決定。由此,，可以搜索窗函數(shù)寬度的合適值：首先計算跳頻信號的模糊函數(shù),，然后在頻移中心位置，沿著時延方向搜索幅值變化得到自項的寬度，即,。?

4? 仿真實驗結(jié)果?

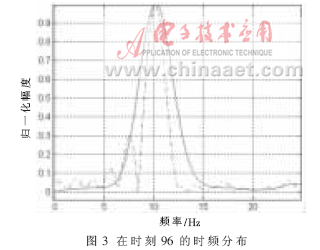
??? 圖2給出了SPWVD分布的核函數(shù)以及設(shè)計核函數(shù)的等高線圖,。與圖1信號模糊函數(shù)的自項相比較，設(shè)計核函數(shù)在形狀上與信號自項更為匹配：主瓣沿著頻移方向較窄而在時延方向較寬,，從而更好地在抑制交叉項的同時保留自項能量,。圖3給出了在時間抽樣等于96時兩種時頻分布的時頻聚集性表示，可以明顯看出新核函數(shù)比SPWVD具有更窄的主瓣寬度,。

?

?

?

??? 通過在信號中加入不同信噪比的高斯白噪聲,，在-10dB～+15dB范圍內(nèi)對每個信噪比做500次實驗，求出跳頻信號參數(shù)估計的性能曲線（參數(shù)估計算法參見文獻(xiàn)[6]）,，見圖4,。從圖中可以看出，在頻率估計方差基本相同的情況下,，跳周期估計的信噪比閾值降低了1dB,，而且隨著信噪比的增加，各個參數(shù)的估計方差比SPWVD都相應(yīng)減小,，證明了算法的有效性,。

?

?

??? 由于跳頻信號頻率變化的非線性，二次型時頻表示具有嚴(yán)重的交叉項干擾,?；谔l信號模糊域自項分析，本文提出了一種新的時頻表示方法,。該方法在抑制交叉項的同時可以保留盡可能多的自項能量,。與SPWVD方法相比，基于新核函數(shù)設(shè)計的跳頻信號時頻分析具有更高的時頻聚集性,，應(yīng)用于信號參數(shù)估計具有更好的性能,。?

參考文獻(xiàn)?

[1] COHEN L. Time-frequency??distributions-A review [J].Proc. IEEE, 1989,(77):941-981.?

[2]?FLANDRIN P. Some features?of time-frequency representations of multicomponent?signals[C].Proc. IEEE 1984?internat. Comf.Acoust. Speech Signal Processing?(ICASSP84), San Diego, CA, March 1984, 41B:1-4.?

[3] FLANDRIN P, MARTIN W. Pseudo-wigner estimators for the analysis of nonstationary processes[C]. Proc. IEEE??Spectr. Est. Workshop II, Tampa, FL,November 1983:?181-185.?

[4] HLAWATSCH F, MANICKAM T G. Smoothed pseudowigner distribution, Choi-Williams distribution, and conekernel representation: Ambiguity-domain analysis and??experimental comparison[J]. Signal Processing, 1995,43:149-168.?

[5] BARBAROSSA S. Parameter estimation of spread spectrum ? frequency hopping signals using? time-frequency distributions[A]. First IEEE Signal Processing Working on Signal?Processing Advances in Wireless Communications. 1997：213-216.?

[6] 趙俊, 張朝陽,賴?yán)?等. 一種基于時頻分析的跳頻信號參數(shù)盲估計方法[J]. 電路與系統(tǒng)學(xué)報,2003,8(3):46-50.?

[7] 張曦, 杜興民, 朱禮亞.基于重排SPWVD的跳頻信號參數(shù)提取方法[J]. 計算機(jī)工程與應(yīng)用, 2007,43(15):144-147.?

[8] HENRY K K, JONES D L. Improved instantaneous?frequency estimation using an adaptive short-time Fourier?transform [J]. IEEE transactions on signal processing,2000,48(10):2964-2972.?

[9] STANKOVIC L, KATKOVNIK V. Algorithm for the in?stantaneous frequency estimation using time-frequency?distributions with adaptive window width [J]. IEEE Signal?Process. Lett， 1998,5(9):207-223.