0 引言
    積分作用從某種意義上來說是人的記憶功能的模擬,。對(duì)人而言,，記憶功能具有某種選擇性,；在控制中,，人總是有選擇地記憶有用的信息而不記憶無用的信息。根據(jù)這一發(fā)現(xiàn),，周其鑒于1983年提出了著名的仿人智能積分控制算法：

  
    其中：u-控制輸出,；Kp-比例系數(shù)；k-抑制系數(shù),；e-誤差,；e-誤差變化率；em,i-誤差第i次峰值,。
    但是,，信息的有用性是相對(duì)的，當(dāng)時(shí)過境遷時(shí),，原來一些有用的信息會(huì)變成無用,。這時(shí)除了不記憶當(dāng)前無用的信息外還會(huì)遺忘那些原來有用而當(dāng)前變得無用的信息。因此,，仿人智能積分控制中的積分作用除表現(xiàn)人的記憶與不記憶兩種行為外,，還應(yīng)該加上遺忘行為。

1 仿人智能積分控制
    常規(guī)PID控制中的積分作用,，不加選擇地“記憶”了誤差及誤差變化的所有信息,，其中也包含了對(duì)控制不利的信息。因此,，這種積分作用缺乏智能性,，其對(duì)誤差的積分過程如圖1所示，且這種積分作用的針對(duì)性不強(qiáng),，甚至有時(shí)不符合控制系統(tǒng)的客觀需要,，只要誤差存在就一直進(jìn)行積分，造成“積分飽和”,。

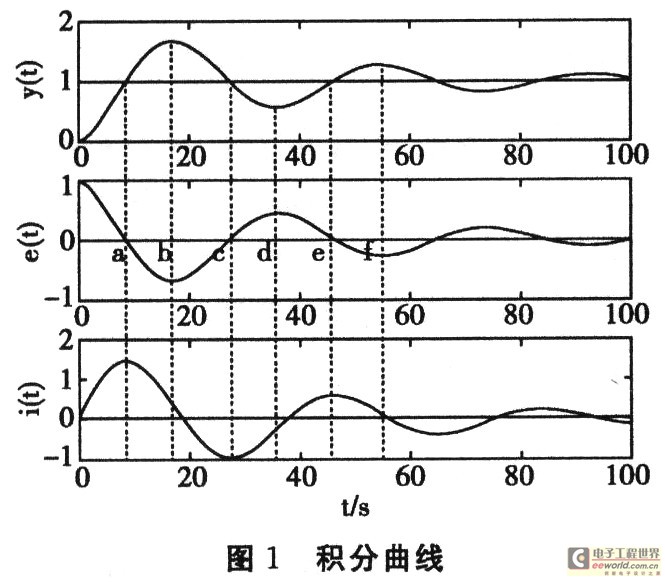
    在積分曲線的(c,，d)段,，積分作用增加一個(gè)正量的控制有利減小回調(diào)，但在(d,，e)區(qū)間積分作用繼續(xù)增強(qiáng),，其結(jié)果勢(shì)必造成系統(tǒng)再次出現(xiàn)超調(diào)，這時(shí)的I控制作用對(duì)系統(tǒng)有害無利,。為了克服這種積分控制作用的缺點(diǎn),，滿足ee>0，加上積分作用,。這樣,，積分控制作用及時(shí)給出合適的附加控制量，能有效地抑制系統(tǒng)誤差的增加,，而在ee>0時(shí),，取消積分作用，使系統(tǒng)借助慣性向穩(wěn)態(tài)過渡,。

2 反積分仿人智能控制
    從動(dòng)力學(xué)角度來看,，系統(tǒng)誤差的產(chǎn)生是由能量不平衡而導(dǎo)致系統(tǒng)應(yīng)有能量損失的一種表現(xiàn)。在系統(tǒng)控制時(shí),，比例作用的主要目的是建立系統(tǒng)新的能量平衡,，而積分作用的主要目的是彌補(bǔ)系統(tǒng)中應(yīng)有的能量積累。因此,，良好的控制應(yīng)該預(yù)先補(bǔ)充較多的能量盡快地使系統(tǒng)恢復(fù)，再在系統(tǒng)恢復(fù)的過程中逐步退回一些原來補(bǔ)人太多的能量,，避免引起系統(tǒng)超調(diào),。為了使積分作用更加合理，在誤差增大區(qū)間施以較強(qiáng)的積分而在誤差減小時(shí)則應(yīng)施以適當(dāng)?shù)姆聪蚍e分使多余積分退出,。這樣,，系統(tǒng)在達(dá)到新的平衡時(shí)保持應(yīng)有的能量。
    實(shí)際上,，仿人智能積分控制從某種角度來說,，不僅具有常規(guī)的積分功能，還具有類似于微分的功能,，并且,，這種用智能積分來體現(xiàn)微分功能的控制既敏感了誤差的變化趨勢(shì)又不像微分那樣對(duì)噪聲也非常敏感。因此,，采用仿人智能積分控制時(shí)一般不需要再加微分作用,。由圖2可見，在AB與CD兩個(gè)區(qū)間,，反積分仿人智能控制和仿人智能積分控制的積分作用基本相同,，主要體現(xiàn)常規(guī)積分作用,，但在：BC與DE兩個(gè)區(qū)間，只有反積分仿人智能控制的積分與微分的趨勢(shì)保持一致,，因此更好地體現(xiàn)了微分功能,。表現(xiàn)在控制方面，則是控制器觀察到誤差將以某個(gè)速度通過誤差零點(diǎn)時(shí),，將采取拉力的作用方式以防止大的超調(diào)量,，在相平面內(nèi)，D控制作用實(shí)際就是誤差的相軌跡,。因此應(yīng)削弱控制初期D控制的作用,；當(dāng)誤差接近0時(shí)，則加強(qiáng)其作用,，使D控制作用主要在誤差較小時(shí)起作用,。

3 改進(jìn)仿人智能控制
    綜合上述分析可知，合理的積分調(diào)節(jié)系數(shù)應(yīng)該是：
    在ee>0區(qū)間上,，在誤差較大時(shí),，希望積分增益參數(shù)KI不要太大，否則∫edt產(chǎn)生較大的值,，響應(yīng)產(chǎn)生振蕩,；在誤差較小時(shí)，希望積分增益增大,，以消除系統(tǒng)的穩(wěn)態(tài)誤差,。期望的積分增益的變化可選取如圖2所示的曲線。
    據(jù)此構(gòu)造如下非線性函數(shù)：
   

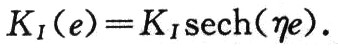
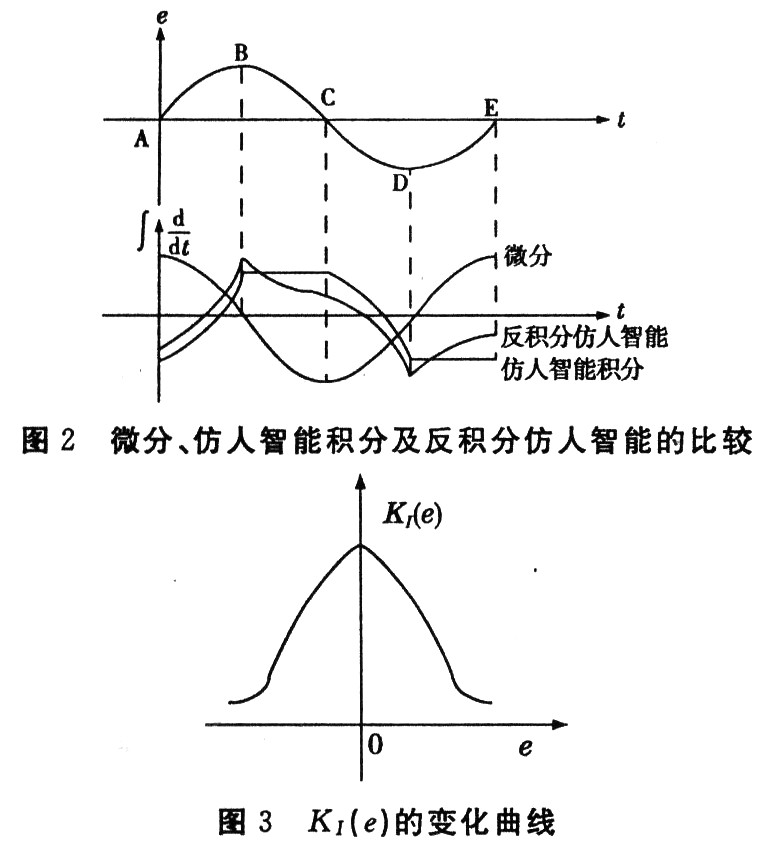
   在ee<0區(qū)間上,，使用仿人智能反向積分作用以使系統(tǒng)的超調(diào)減少,，此區(qū)間反積分調(diào)節(jié)系數(shù)與微分調(diào)節(jié)規(guī)律相似；在誤差較大時(shí),，反積分系數(shù)不要太大,，避免減弱P控制作用；在誤差較小時(shí),，則加強(qiáng)反積分作用,。
    據(jù)此構(gòu)造如圖的構(gòu)造函數(shù)，得到如下改進(jìn)仿人智能算法：

  
    式中,，KI+(e)=KI+sech(αe),；KI-(e)=KI-sech(βe)；其余參數(shù)均同(1),，(2)式說明,。

4 仿真研究
    為了檢驗(yàn)所設(shè)計(jì)系統(tǒng)的控制品質(zhì)，在單位階躍輸入作用下,，對(duì)工業(yè)工程中普遍存在的二階加純滯后對(duì)象進(jìn)行仿真,，仿真分別在滯后較小和較大兩種情況下進(jìn)行,，并與PID控制器進(jìn)行比較。下述各圖實(shí)線為仿人智能控制結(jié)果,，虛線為PID控制結(jié)果,。

  (1)當(dāng)滯后較小時(shí)：
    被控對(duì)象傳遞函數(shù)為(采樣時(shí)間為1秒)：
  

    仿人智能控制器參數(shù)：Kp=1．3、k=0．8,、KI+=0．001,、KI-=-0．002、α=1,、β=0．7,；PID控制器參數(shù)為：P=0．2、I=0．15,、D=0．2,。仿真結(jié)果如圖4所示。

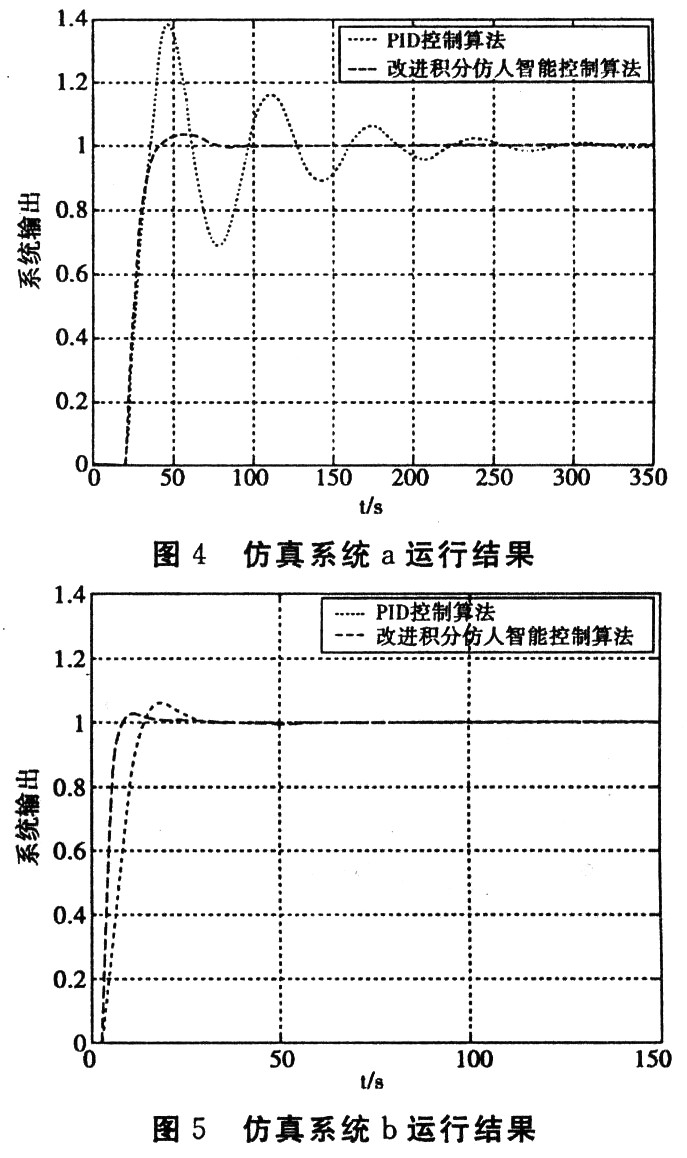
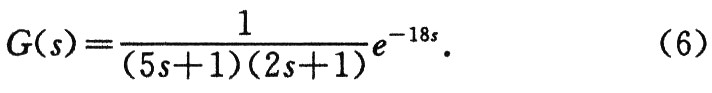
    仿人智能控制器參數(shù)為：Kp=1．3,、k=0．8,、KI+=0．6、KI-=-0．02,、α=1,、β=0．7；PID控制器參數(shù)為：P=0．3,、I=0．04,、D=0．08。仿真結(jié)果如圖5所示,。

5 結(jié)束語
    本文在仿人智能積分控制算法和反積分仿人智能控制算法的基礎(chǔ)上構(gòu)造了系統(tǒng)的非線性積分系數(shù)和實(shí)時(shí)整定積分系數(shù),，通過仿真結(jié)果得知：改進(jìn)的仿人智能控制器對(duì)對(duì)象參數(shù)變化不是很敏感，并且對(duì)具有大延遲的對(duì)象,，不論在穩(wěn)定性,、快速性以及準(zhǔn)確性方面都比PID控制具有明顯的優(yōu)越性,。而且隨著τ／T的增加,，即系統(tǒng)的可控性越來越強(qiáng)，改進(jìn)的仿人智能控制的優(yōu)越性就越明顯,。