在現(xiàn)代戰(zhàn)爭中,，隨著精確制導(dǎo)武器的廣泛使用,，飛行控制技術(shù)的研究已日趨深入和普及?？盏貙?dǎo)彈在飛行過程中因彈道設(shè)計(jì)的需要一般分為滑翔,、點(diǎn)火、轉(zhuǎn)彎,、俯沖等多個階段,，而每個階段均對應(yīng)幾個或多個特征點(diǎn)。根據(jù)特征點(diǎn)的不同可把彈道劃分為多個時間段,，每個時間段對應(yīng)不同的控制律,，所以在相鄰時間段的臨界點(diǎn)，其控制系數(shù)會發(fā)生跳變,。這將造成計(jì)算結(jié)果(控制量)在該點(diǎn)的突變,，從而影響彈體的穩(wěn)定飛行。這里論述了某無動力彈的飛行控制系統(tǒng)中解算控制率的方法,，以及對其彈道臨界點(diǎn)的平滑處理,，并用數(shù)字信號處理器對其算法進(jìn)行了工程實(shí)現(xiàn)。
2 用PID算法計(jì)算控制率
比例積分微分控制器(簡稱PID)控制簡單,、可靠,，物理意義明顯，在工程實(shí)踐中已廣泛采用,。PID控制器由比例單元,、積分單元和微分單元組成。其輸入e(t)與輸出u(t)的關(guān)系為：
在無動力空地導(dǎo)彈飛行控制過程中,，飛行姿態(tài)誤差信號分別為俯仰角誤差θ(t),、偏航角誤差ψ(t)和滾轉(zhuǎn)角誤差γ(t)。位置誤差信號分別為：高度誤差日(t),、偏航誤差Z(t)和縱向誤差X(t),。鉆地航彈通過改變俯仰角V1、偏航角V2,、滾轉(zhuǎn)角V3來減小姿態(tài)誤差和位置誤差,。因此,，PID控制的輸入為θ(t)，ψ(t),，γ(t),，H(t)，Z(t),，X(t),，輸出為V1(t)，V2(t),，V3(t),。根據(jù)飛行力學(xué)中姿態(tài)角誤差與位置誤差的因果關(guān)系，并將PID控制關(guān)系式離散化,，得到輸入與輸出的關(guān)系為：
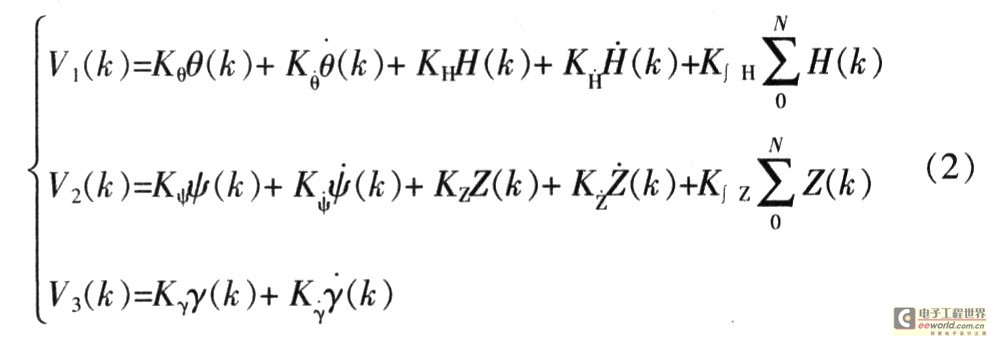
式中：所有K都是經(jīng)過仿真后得到的各特征點(diǎn)的PID系數(shù),。
以上捕述的數(shù)學(xué)模型又稱為位置型PID算法，該算法有很大的局限性,，利用該算法容易產(chǎn)生積分項(xiàng)溢出,。如果將計(jì)算的控制率直接用于控制回路，會造成控制回路的失穩(wěn),。另外,，由于鉆地航彈的姿態(tài)角與位置的改變滯后于舵機(jī)的變化，況且由于受到航彈操縱性的影響,，彈道誤差也不可能瞬間消除,，所以很有可能在較長的一段時間內(nèi)彈道誤差始終為正或?yàn)樨?fù)。圖l給出一段時間內(nèi)的彈道軌跡,。
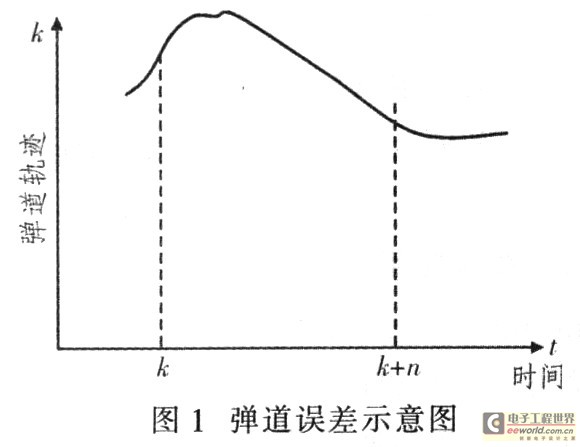
圖l中,，虛線為方案彈道，實(shí)線為真實(shí)彈道,。在k△t和(k+n)△t時刻,，彈道誤差為0，在兩個時刻間的n個點(diǎn),，真實(shí)彈道與方案彈道的差均為正值,。此時，積分項(xiàng)
有可能較大,，直至溢出。況且計(jì)算控制率時只考慮到當(dāng)前的彈道誤差和姿態(tài)誤差,，而沒有考慮到前一點(diǎn)的控制率,，有可能使得V(k)一V(k一1)比較大，按照該控制率操縱彈的飛行,，使得鉆地彈飛行時產(chǎn)生劇烈的振蕩,，影響鉆地彈的穩(wěn)定飛行,。所以利用該算法求解控制率時有一定的局限性，現(xiàn)討論改進(jìn)型的PID算法一增量性PID算法,。
將式(1)離散化可得：
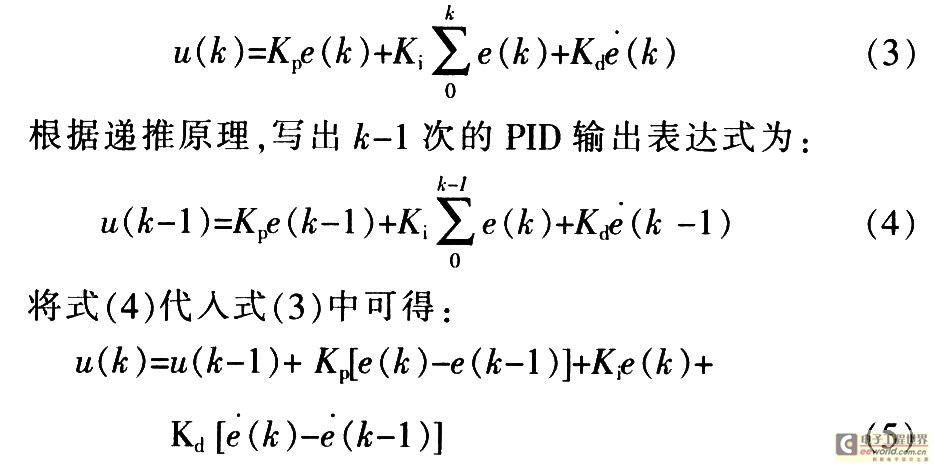
由式(5)可知,，當(dāng)前的輸出誤差由前一點(diǎn)的輸出誤差、輸入誤差和當(dāng)前的輸入誤差組成,，表明了一個遞推關(guān)系,，所以稱為增量性的PID控制。
將式(5)改寫成增量性的遞推關(guān)系．有：
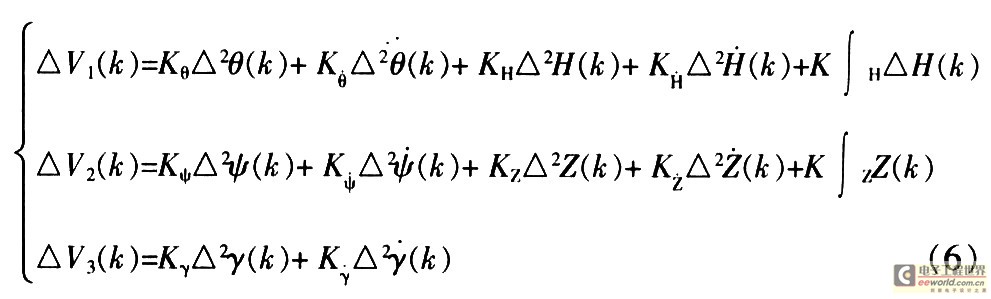
3 臨界點(diǎn)的平滑處理
在彈體的飛行過程中,，不同飛行段的PID控制系數(shù)不同,，在不同飛行段，PID系數(shù)甚至相差約10倍,，所以臨界點(diǎn)的控制變量按照式(6)計(jì)算時會出現(xiàn)較大的增量,，把算出的臨界點(diǎn)的控制變量帶入舵機(jī)控制，會給彈體的穩(wěn)定飛行帶來很大的影響,。所以合理處理臨界點(diǎn)的控制變量也是保證彈體穩(wěn)定飛行的一個重要環(huán)節(jié),。
處理臨界點(diǎn)的控制律有2種方法。一是限幅原理,，即每次的控制增量不大于5°,。這種方法被貫穿在所有點(diǎn)的控制變量解算過程中。該方法原理簡單,，但僅是粗線條地限制了控制率增量不能過大,，不能正確反映控制變量的變化趨勢；二是采用加權(quán)平均法處理臨界點(diǎn)附近的控制變量,，使得控制變量曲線比較平滑,，而且臨界點(diǎn)的控制變量前后具有延續(xù)性。避免了產(chǎn)生較大增量影響彈體的穩(wěn)定飛行,。
加權(quán)平均法的處理思想是對n項(xiàng)采樣結(jié)果取不同的權(quán)重,，然后相加，其具體的計(jì)算方法為：
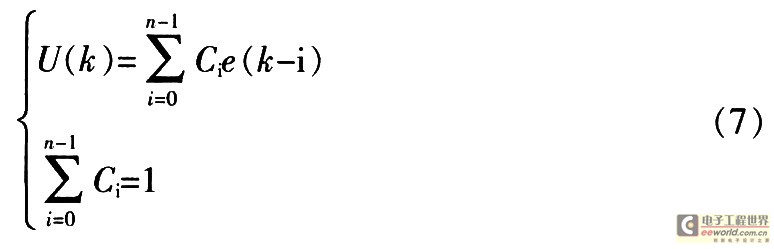
式中：C0,，C1,，…，Cn-1為各次采樣系數(shù),，體現(xiàn)了各次采樣值在平均值中所占的比例,。
一般而言，采樣次數(shù)愈靠后,，取的比例愈大,，這樣可增加新的采樣值在平均值中的比例。該方法可根據(jù)需要突出信號的某一部分,，抑制信號的另一部分,。
在此采用8點(diǎn)加權(quán)平均法計(jì)算跨臨界點(diǎn)的控制變量,。如果計(jì)算k點(diǎn)的控制變量，則選用8個點(diǎn)的加權(quán)系數(shù),，即：
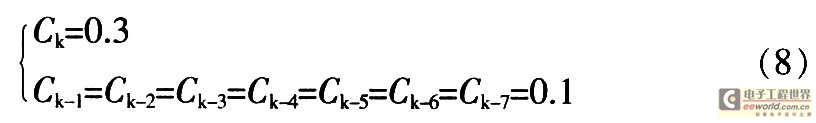
這里,，采用加權(quán)平均法處理臨界點(diǎn)及臨界點(diǎn)前7個點(diǎn)的控制變量。從而把臨界點(diǎn)突兀的控制增量變?yōu)闈u緩的控制率增量,。
4 系統(tǒng)的工程實(shí)現(xiàn)
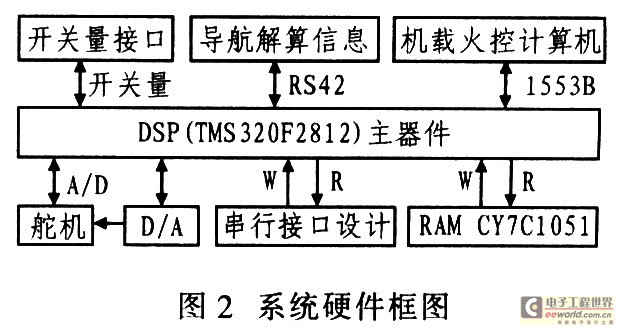
該系統(tǒng)采用TI公司的TMS320F2812作為CPU,，用以實(shí)現(xiàn)計(jì)算、通信,、數(shù)據(jù)存貯,、舵機(jī)控制等功能。該器件的工作頻率為150 MHz,，能夠在較短的時間內(nèi)(幾十微秒)完成控制變量的計(jì)算,。圖2給出該系統(tǒng)的硬件框圖。
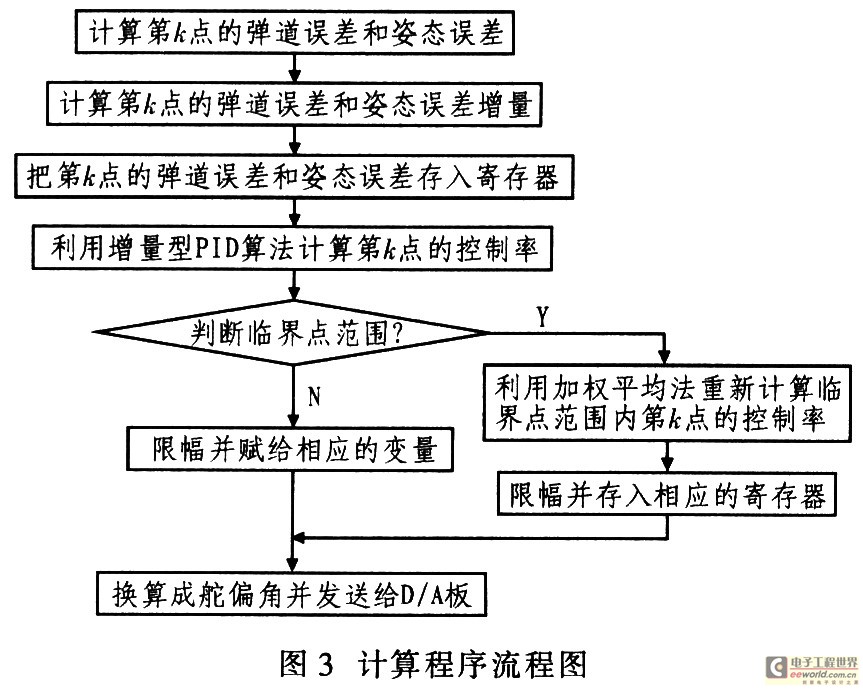
計(jì)算程序所要完成的主要工作是計(jì)算控制率,，并把控制增量轉(zhuǎn)化為舵機(jī)的偏轉(zhuǎn)角,。根據(jù)增量型PID算法和處理臨界點(diǎn)的加權(quán)平均法計(jì)算控制率和舵機(jī)偏轉(zhuǎn)角。在實(shí)際加權(quán)平均法計(jì)算中,，為了提高速度,，借鑒滑動濾波的處理方法，即先在RAM中建立一個數(shù)據(jù)緩沖區(qū),，依順序存放8個采樣數(shù)據(jù),，每采進(jìn)一個數(shù)據(jù)，就將最早采集的那個數(shù)據(jù)丟掉,，而后求含新數(shù)據(jù)在內(nèi)的8個數(shù)據(jù)的加權(quán)平均值,。這樣即可加快數(shù)據(jù)處理的速度。圖3給出其程序流程圖,。
5 實(shí)驗(yàn)及結(jié)論
圖4給出某次實(shí)驗(yàn)中通過增量型PID算法計(jì)算出飛行過程中每個點(diǎn)的控制變量曲線,。由圖4(a)可知，未經(jīng)平滑的控制變量變化較大,，尤其是在臨界點(diǎn)上控制變量發(fā)生躍變,，從而使彈體失控，造成災(zāi)難性的后果,。圖4(b)給出通過限幅和加權(quán)平均法進(jìn)行平滑處理后的控制變量曲線,。
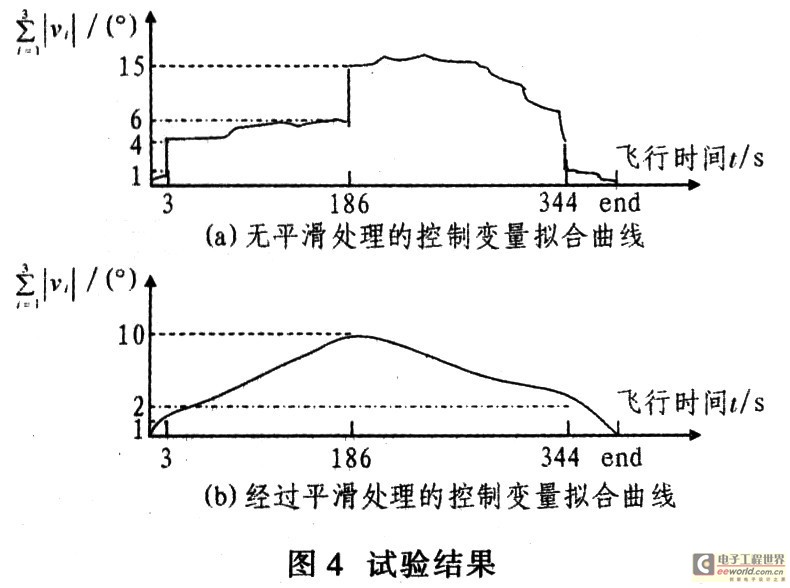
由圖4(b)可見，控制變量較為平滑,。這樣的處理結(jié)果,，使得彈道上相鄰兩個點(diǎn)的控制增量較小，即每次彈體飛行調(diào)整的姿態(tài)角較小，從而使彈體飛行所需的過載較小,，保障了無動力彈的穩(wěn)定飛行。