折合到輸入端噪聲(代碼躍遷噪聲)

　　實(shí)際的ADC在許多方面與理想的ADC有偏差,。折合到輸入端的噪聲肯定不是理想情況下會(huì)出現(xiàn)的，它對ADC整體傳遞函數(shù)的影響如圖1所示,。隨著模擬輸入電壓提高,，"理想"ADC(如圖1A所示)保持恒定的輸出代碼，直至達(dá)到躍遷區(qū),，此時(shí)輸出代碼即刻跳變?yōu)橄乱粋€(gè)值,，并且保持該值，直至達(dá)到下一個(gè)躍遷區(qū),。理論上,，理想ADC的"代碼躍遷"噪聲為0，躍遷區(qū)寬度也等于0.實(shí)際的ADC具有一定量的代碼躍遷噪聲,，因此躍遷區(qū)寬度取決于折合到輸入端噪聲的量(如圖1B所示),。圖1B顯示的情況是代碼躍遷噪聲的寬度約為1個(gè)LSB(最低有效位)峰峰值。

圖1:代碼躍遷噪聲(折合到輸入端噪聲)及其對ADC傳遞函數(shù)的影響

　　由于電阻噪聲和"kT/C"噪聲,，所有ADC內(nèi)部電路都會(huì)產(chǎn)生一定量的均方根(RMS)噪聲,。即使是直流輸入信號(hào),，此噪聲也存在，它是代碼躍遷噪聲存在的原因,。如今通常把代碼躍遷噪聲稱為"折合到輸入端噪聲",，而不是直接使用"代碼躍遷噪聲"這一說法。折合到輸入端噪聲通常用ADC輸入為直流值時(shí)的若干輸出樣本的直方圖來表征,。大多數(shù)高速或高分辨率ADC的輸出為一系列以直流輸入標(biāo)稱值為中心的代碼(見圖2),。為了測量其值，ADC的輸入端接地或連接到一個(gè)深度去耦的電壓源,，然后采集大量輸出樣本并將其表示為直方圖(有時(shí)也稱為"接地輸入"直方圖),。由于噪聲大致呈高斯分布，因此可以計(jì)算直方圖的標(biāo)準(zhǔn)差σ,，它對應(yīng)于有效輸入均方根噪聲,。參考文獻(xiàn)1詳細(xì)說明了如何根據(jù)直方圖數(shù)據(jù)計(jì)算σ值。該均方根噪聲雖然可以表示為以ADC滿量程輸入范圍為基準(zhǔn)的均方根電壓,，但慣例是用LSBrms來表示,。

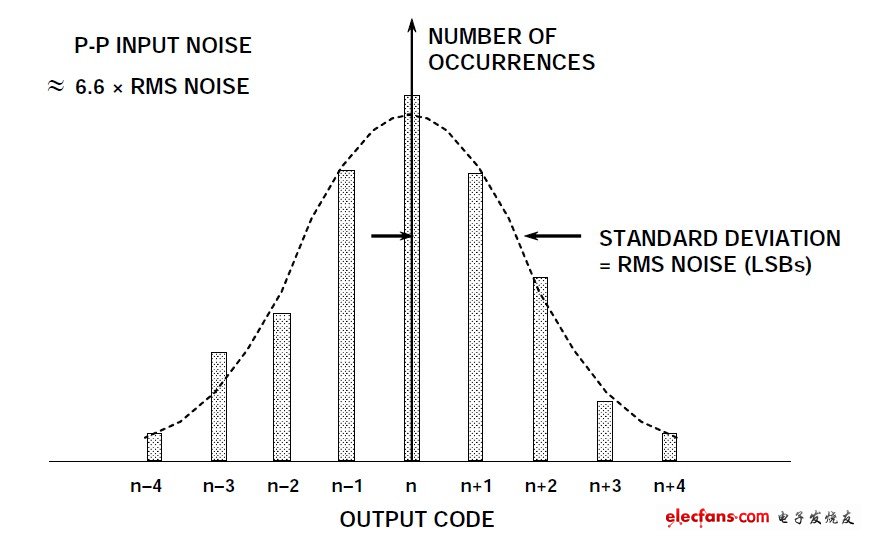
圖2:折合到輸入端噪聲對ADC"接地輸入端"直方圖的影響(ADC具有少量DNL)

　　雖然ADC固有的微分非線性(DNL)可能會(huì)導(dǎo)致其噪聲分布與理想的高斯分布有細(xì)微的偏差(圖2示例中顯示了部分DNL)，但它至少大致呈高斯分布,。如果DNL比較大,，則應(yīng)計(jì)算多個(gè)不同直流輸入電壓的值，然后求平均值,。例如,，如果代碼分布具有較大且獨(dú)特的峰值和谷值，則表明ADC設(shè)計(jì)不佳,，或者更有可能的是PCB布局布線錯(cuò)誤,、接地不良、電源去耦不當(dāng)(見圖3),。當(dāng)直流輸入掃過ADC輸入電壓范圍時(shí),，如果分布寬度急劇變化，這也表明存在問題,。

圖3:設(shè)計(jì)不佳的ADC和/或布局布線,、接地,、去耦不當(dāng)?shù)慕拥剌斎攵酥狈綀D

　　無噪聲(無閃爍)代碼分辨率

　　ADC的無噪聲代碼分辨率是指這樣一個(gè)位數(shù)，如果超過該位數(shù),，則無法明確無誤地解析各個(gè)代碼,，原因是存在所有ADC都具有的有效輸入噪聲(或折合到輸入端噪聲)，如上文所述,。該噪聲可以表示為均方根量,，單位通常是LSBrms.乘以系數(shù)6.6可以將均方根噪聲轉(zhuǎn)換為峰峰值噪聲(用"LSB峰峰值"表示),。N位ADC的總范圍為2NLSB.因此，無噪聲采樣總數(shù)等于：

　　對無噪聲采樣數(shù)求以2為底的對數(shù)可以得到無噪聲代碼分辨率：

　　無噪聲代碼分辨率規(guī)格一般與高分辨率-型測量ADC相關(guān),，通常是采樣速率,、數(shù)字濾波器帶寬和可編程增益放大器(PGA)增益的函數(shù)。圖4所示為從-型測量ADCAD7730獲得的一個(gè)典型數(shù)據(jù)表,。

圖4:Σ-Δ型ADCAD7730的無噪聲代碼分辨率

　　注意,，當(dāng)輸出數(shù)據(jù)速率為50Hz、輸入范圍為±10mV時(shí),，無噪聲代碼分辨率為16.5位(80,，000無噪聲采樣)。這些條件下的建立時(shí)間為460ms,，因此該ADC是精密電子秤應(yīng)用的理想之選,。對于適合精密測量應(yīng)用的高分辨率-型ADC，大部分?jǐn)?shù)據(jù)手冊都提供了類似的數(shù)據(jù),。

　　有時(shí)候會(huì)利用滿量程范圍與均方根輸入噪聲(而非峰峰值噪聲)的比值來計(jì)算分辨率,，該分辨率稱為"有效分辨率".注意：在相同條件下，有效分辨率比無噪聲代碼分辨率高log2(6.6),，約2.7位,。

　　有些制造商更愿意規(guī)定有效分辨率,，而不是無噪聲代碼分辨率,，因?yàn)榍罢叩奈粩?shù)較高。用戶應(yīng)仔細(xì)檢查數(shù)據(jù)手冊,，弄清它到底指定哪一種分辨率,。

　　通過數(shù)字均值法提高ADC分辨率并降低噪聲

　　折合到輸入端噪聲的影響可以通過數(shù)字均值方法降低。假設(shè)一個(gè)16位ADC具有15位無噪聲分辨率,，采樣速率為100kSPS.對于每個(gè)輸出樣本,，如果對兩個(gè)樣本進(jìn)行平均，則有效采樣速率降至50kSPS,，SNR提高3dB,，無噪聲位數(shù)提高到15.5位。如果對四個(gè)樣本進(jìn)行平均,，則采樣速率降至25kSPS,，SNR提高6dB，無噪聲位數(shù)提高到16位,。

　　事實(shí)上,，如果對16個(gè)樣本進(jìn)行平均，則輸出采樣速率降至6.25kSPS,，SNR再提高6dB,，無噪聲位數(shù)提高到17位,。為了利用額外的"分辨率"，均值算法必須在較大的有效位數(shù)上執(zhí)行,。

　　均值過程還有助于消除ADC傳遞函數(shù)的DNL誤差,，這可以通過下面的簡單例子來說明：假設(shè)ADC在量化電平"k"處有一個(gè)失碼，雖然代碼"k"由于DNL誤差較大而丟失,，但兩個(gè)相鄰代碼k–1和k+1的平均值等于k.

　　因此,，可以利用該技術(shù)來有效提高ADC的動(dòng)態(tài)范圍，代價(jià)是整體輸出采樣速率降低并且需要額外的數(shù)字硬件,。不過應(yīng)注意,，均值并不能校正ADC固有的積分非線性。

　　現(xiàn)在考慮這樣一種情況：ADC的折合到輸入端噪聲非常低,，直方圖總是顯示一個(gè)明確的代碼,，對于這種ADC，數(shù)字均值有何作用呢?答案很簡單--沒有作用!無論對多少樣本進(jìn)行平均,，答案始終相同,。但只要將足夠大的噪聲增加到輸入信號(hào)中，使得直方圖中有一個(gè)以上的代碼,，那么均值方法又會(huì)發(fā)揮效用,。因此，少量噪聲可能是好事情(至少對于均值方法而言),，但輸入端存在的噪聲越高,，為實(shí)現(xiàn)相同分辨率所需的均值樣本數(shù)越多。

　　切勿將有效位數(shù)(ENOB)與有效分辨率或無噪聲代碼分辨率混為一談

　　由于這些術(shù)語名稱相似,，"有效位數(shù)"和"有效分辨率"常被誤認(rèn)為是一回事,，事實(shí)并非如此。

　　有效位數(shù)(ENOB)來自對ADC輸出的FFT分析,，條件是用一個(gè)滿量程正弦波輸入信號(hào)激勵(lì)A(yù)DC.計(jì)算所有噪聲和失真項(xiàng)的和方根(RSS)值,，信號(hào)對噪聲和失真的比值定義為信納比SINAD或S/(N+D)。理想N位ADC的理論SNR為：

　　將計(jì)算所得的SINAD值替換等式5中的SNR,，并求解N,，便得到ENOB:

　　用于計(jì)算SINAD和ENOB的噪聲和失真不僅包括折合到輸入端噪聲，而且包括量化噪聲和失真項(xiàng),。SINAD和ENOB用于衡量ADC的動(dòng)態(tài)性能,，有效分辨率和無噪聲代碼分辨率則用于衡量ADC在無量化噪聲的直流輸入條件下的噪聲。

　　利用噪聲擾動(dòng)提高ADC無雜散動(dòng)態(tài)范圍

　　對于高速ADC,，若要最大程度地提高SFDR,，存在兩個(gè)基本限制：第一是前端放大器和采樣保持電路產(chǎn)生的失真;第二是ADC編碼器部分的實(shí)際傳遞函數(shù)的非線性所導(dǎo)致的失真。

　　提高SFDR的關(guān)鍵是盡可能降低以上兩種非線性。

　　要顯著降低ADC前端引起的固有失真,，在ADC外部著力是徒勞的,。然而，ADC編碼器傳遞函數(shù)的微分非線性可以通過適當(dāng)利用擾動(dòng)(即外部噪聲,，與ADC的模擬輸入信號(hào)相加)來降低,。

　　在一定的條件下，擾動(dòng)可以改善ADC的SFDR(參考文獻(xiàn)2-5),。例如,，即使在理想ADC中，量化噪聲與輸入信號(hào)也有某種相關(guān)性,，這會(huì)降低ADC的SFDR,，特別是當(dāng)輸入信號(hào)恰好為采樣頻率的約數(shù)時(shí)。將寬帶噪聲(幅度約為LSBrms)與輸入信號(hào)相加往往會(huì)使量化噪聲隨機(jī)化,，從而降低其影響(見圖5A),。然而，在大多數(shù)系統(tǒng)中,，信號(hào)之上有足夠的噪聲,，因此無需額外添加擾動(dòng)噪聲。ADC的折合到輸入端噪聲也可能足以產(chǎn)生同樣的效果,。將寬帶均方根噪聲電平提高約1LSB以上會(huì)成比例地降低ADCSNR,，且性能不會(huì)有進(jìn)一步的提高。

　　還有其它一些方案,，都使用更大數(shù)量的擾動(dòng)噪聲,，使ADC的傳遞函數(shù)隨機(jī)化。圖5B還顯示了一個(gè)由驅(qū)動(dòng)DAC的偽隨機(jī)數(shù)發(fā)生器組成的擾動(dòng)噪聲源,，此信號(hào)從ADC輸入信號(hào)中減去后,，以數(shù)字方式增加到ADC輸出中,，從而不會(huì)導(dǎo)致SNR性能顯著下降,。這種技術(shù)本身有一個(gè)缺點(diǎn)，即隨著擾動(dòng)信號(hào)的幅度增大,，允許的輸入信號(hào)擺幅會(huì)減小,。之所以需要減小信號(hào)幅度，是為了防止過驅(qū)ADC.應(yīng)當(dāng)注意,，這種方案不能顯著改善ADC前端產(chǎn)生的失真,，只能改善ADC編碼器傳遞函數(shù)的非線性所引起的失真。

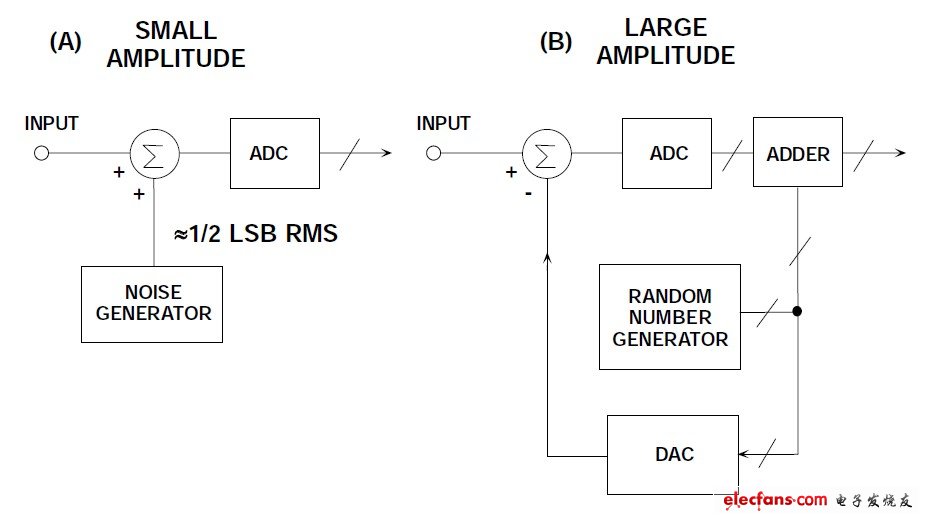
圖5:利用擾動(dòng)使ADC傳遞函數(shù)隨機(jī)化

　　還有一種方法更容易實(shí)現(xiàn),，尤其是在寬帶接收機(jī)中,，即注入信號(hào)目標(biāo)頻帶以外的一個(gè)窄帶擾動(dòng)信號(hào)，如圖6所示,。一般來說,，信號(hào)成分不會(huì)位于接近DC的頻率范圍,，因此該低頻區(qū)常用于這種擾動(dòng)信號(hào)。擾動(dòng)信號(hào)可能還位于略低于fs/2的地方,。相對于信號(hào)帶寬,，擾動(dòng)信號(hào)僅占用很小的帶寬(數(shù)百kHz帶寬通常即足夠)，因此SNR性能不會(huì)像在寬帶擾動(dòng)下那樣顯著下降,。

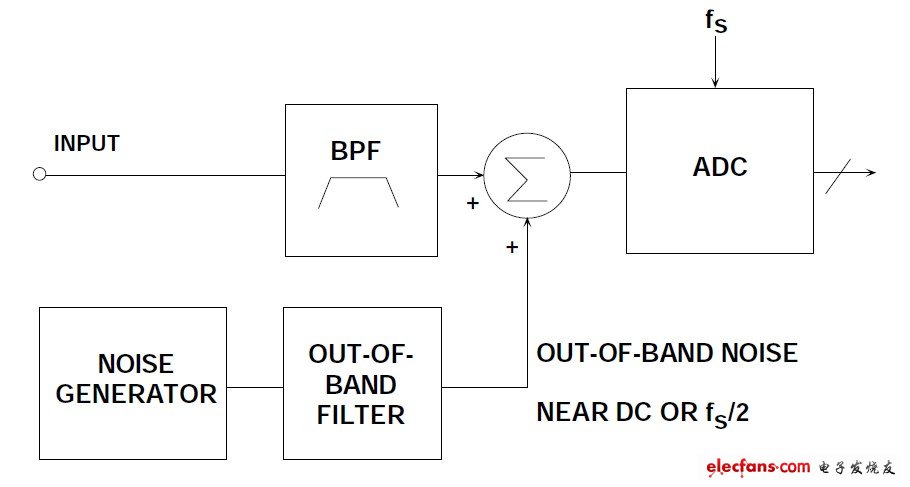
圖6:注入帶外擾動(dòng)以改善ADCSFDR

　　分級(jí)流水線式ADC,，例如圖7所示的14位105MSPSADCAD6645，在ADC范圍內(nèi)的特定代碼躍遷點(diǎn)有非常小的差分非線性誤差,。AD6645由一個(gè)5位ADC1,、一個(gè)5位ADC2和一個(gè)6位ADC3組成。嚴(yán)重的DNL誤差僅出現(xiàn)在ADC1躍遷點(diǎn),，第二級(jí)和第三級(jí)ADC的DNL誤差非常小,。ADC1有25=32個(gè)相關(guān)的決策點(diǎn)，每隔68.75mV(29=512LSB)出現(xiàn)一個(gè)(2.2V滿量程輸入范圍),。圖8以夸張形式顯示了這些非線性誤差,。

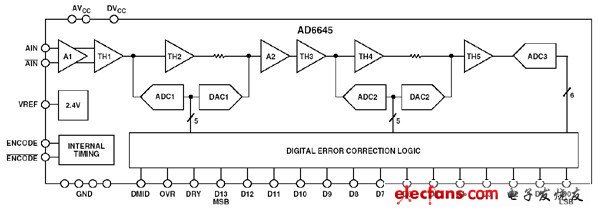
圖7:14位105MSPSADCAD6645簡化框圖

圖8:AD6645分級(jí)點(diǎn)DNL誤差(夸張顯示)

　　對于最高約為200MHz的模擬輸入，AD6645前端產(chǎn)生的失真成分與編碼器產(chǎn)生的失真相比可忽略不計(jì),。這就是說,，AD6645傳遞函數(shù)的靜態(tài)非線性是SFDR性能的主要限制。

　　目標(biāo)是選擇適當(dāng)?shù)膸鈹_動(dòng)量,，使得這些微小DNL誤差的影響在ADC整個(gè)輸入范圍內(nèi)隨機(jī)化,，從而降低平均DNL誤差。這可以通過實(shí)驗(yàn)方法確定,，覆蓋大約兩個(gè)ADC1躍遷區(qū)的峰峰值擾動(dòng)噪聲對DNL的改善最佳,。更高的噪聲量不會(huì)明顯改善DNL.兩個(gè)ADC1躍遷區(qū)覆蓋1024LSB峰峰值，或者大約155LSBrms(峰峰值高斯噪聲除以6.6即得到均方根值),。

　　圖9中的第一幅圖顯示一小部分輸入信號(hào)范圍內(nèi)的無擾動(dòng)DNL.水平軸經(jīng)過放大,，以顯示兩個(gè)相距68.75mV(512LSB)的分級(jí)點(diǎn)。第二幅圖顯示增加155LSBrms擾動(dòng)后的DNL,，該擾動(dòng)量相當(dāng)于大約–20.6dBm.請注意,，DNL得到顯著改善。

圖9:無擾動(dòng)和有擾動(dòng)的AD6645DNL

　　擾動(dòng)噪聲可以通過多種方式產(chǎn)生,?？梢允褂迷肼?font class="f14">二極管，但簡單地放大器寬帶雙極性運(yùn)放的輸入電壓噪聲是更經(jīng)濟(jì)的解決方案,，這種方法已在參考文獻(xiàn)3,、4、5中詳細(xì)說明，在此恕不贅述,。

　　利用帶外擾動(dòng)獲得的SFDR大幅改善結(jié)果如圖10的深(1,，048，576點(diǎn))FFT所示,，其中AD6645以80MSPS的速率對一個(gè)–35dBm,、30.5MHz信號(hào)進(jìn)行采樣。請注意,，無擾動(dòng)時(shí)SFDR約為92dBFS,，有擾動(dòng)時(shí)約為108dBFS，提高幅度達(dá)16dB,！

圖10：無擾動(dòng)和有擾動(dòng)的AD6645FFT圖

　　AD6645ADC由ADI公司于2000年推出,，直到最近，它仍是代表SFDR極致性能的產(chǎn)品,。自從推出該器件后,，工藝技術(shù)和電路設(shè)計(jì)兩方面的進(jìn)步推動(dòng)ADC向更高性能發(fā)展，例如AD9444(14位,、80MSPS),、AD9445(14位、105/125MSPS)和AD9446(16位,、80/100MSPS),，這些ADC具有非常高的SFDR(對于70MHz滿量程輸入信號(hào)，典型值大于90dBc)和低DNL,。

　　在一定的輸入信號(hào)條件下,，增加適當(dāng)?shù)膸鈹_動(dòng)信號(hào)同樣可以改善SFDR性能。

圖11顯示了有擾動(dòng)和無擾動(dòng)下的AD9444(14位,、80MSPS)FFT.在這些輸入條件下,，添加擾動(dòng)使SFDR提高25dB。所示數(shù)據(jù)是利用ADIsimADC程序和AD9444模型獲得,。

　　雖然圖10和圖11所示的結(jié)果相當(dāng)驚人,，但不應(yīng)認(rèn)為，增加帶外噪聲擾動(dòng)一定就會(huì)改善ADC的SFDR,，或者在所有條件下都適用,。正如之前提到的，擾動(dòng)無法改善ADC前端電路的線性度。即使是近乎理想的前端,，擾動(dòng)的效果也將高度依賴于輸入信號(hào)的幅度和擾動(dòng)信號(hào)本身的幅度,。例如，當(dāng)信號(hào)接近ADC的滿量程輸入范圍時(shí),，傳遞函數(shù)的積分非線性可能會(huì)成為確定SFDR的限制因素,，擾動(dòng)將沒有助益。務(wù)必認(rèn)真研究數(shù)據(jù)手冊,，某些情況下,，其中可能給出了有擾動(dòng)和無擾動(dòng)的數(shù)據(jù)以及幅度和帶寬建議。擾動(dòng)可能是更新一代中頻采樣ADC的內(nèi)置特性,。

　　結(jié)束語

　　在本文中,，我們說明了所有ADC都有一定量的折合到輸入端噪聲。在精密,、低頻測量應(yīng)用中,，以數(shù)字方式對ADC輸出數(shù)據(jù)求平均值可以降低該噪聲，代價(jià)是采樣速率會(huì)降低并且需要額外的硬件,。該均值方法實(shí)際上可以提高ADC的分辨率,，但無法降低積分非線性誤差。