摘  要：由于傳感器網(wǎng)絡(luò)所使用無(wú)線信道的共享性和相互干擾，節(jié)點(diǎn)間數(shù)據(jù)廣播會(huì)產(chǎn)生資源沖突,，廣播調(diào)度要解決的即是為每個(gè)節(jié)點(diǎn)分配到一個(gè)無(wú)沖突傳輸時(shí)隙,，其目標(biāo)是找到晟優(yōu)時(shí)分復(fù)用（TDMA：Time division multiple access）調(diào)度解，使得幀長(zhǎng)度最短而信道利用率最大．提出基于神經(jīng)網(wǎng)絡(luò)的兩階段混合廣播調(diào)度算法．在階段一,，使用改進(jìn)的頂點(diǎn)著色算法來(lái)獲得調(diào)度所需最短時(shí)隙數(shù)目,；在階段二，使用模糊Hopfield將節(jié)點(diǎn)模糊聚類(lèi)為M類(lèi),，同類(lèi)節(jié)點(diǎn)可以在同一時(shí)隙被調(diào)度，不同類(lèi)節(jié)點(diǎn)必須在不同時(shí)隙被調(diào)度．用該算法對(duì)3個(gè)測(cè)試拓?fù)鋱D進(jìn)行調(diào)度,，實(shí)驗(yàn)結(jié)果表明該算法比其他算法能獲得更短的幀長(zhǎng)度和更低的網(wǎng)絡(luò)延遲,，證明了所提算法的可行性和有效性．

關(guān)鍵詞：無(wú)線傳感器網(wǎng)絡(luò)；廣播調(diào)度問(wèn)題,；Hopfield神經(jīng)網(wǎng)絡(luò),；圖著色

1  引  言

      在監(jiān)測(cè)區(qū)域內(nèi)，以隨機(jī)方式分布的集成有傳感器,、數(shù)據(jù)處理單元和無(wú)線通信模塊的微小節(jié)點(diǎn)通過(guò)自組織方式便構(gòu)成了無(wú)線傳感器網(wǎng)絡(luò)（WSN） ^[1] ．WSN 中節(jié)點(diǎn)經(jīng)常需要廣播消息或數(shù)據(jù),，用于同步機(jī)制、拓?fù)淇刂苹蚵酚山⑴c維護(hù)等．由于無(wú)線鏈路的共享與開(kāi)放性,，很容易造成消息傳輸時(shí)的相互沖突,，若節(jié)點(diǎn)的多個(gè)相鄰節(jié)點(diǎn)同時(shí)向該節(jié)點(diǎn)廣播消息，則必然產(chǎn)生相互干擾或沖突并造成廣播消息不能正確收發(fā),，大多數(shù)WSN網(wǎng)絡(luò)此時(shí)要求源節(jié)點(diǎn)重傳,，而造成節(jié)點(diǎn)能量額外消耗，從因此需要對(duì)節(jié)點(diǎn)的消息廣播進(jìn)行合理調(diào)度以延長(zhǎng)網(wǎng)絡(luò)壽命^[2] ．大多數(shù)WSN使用時(shí)分復(fù)用（TDMA）作為無(wú)線信道共享與接入方式^[3] ,本文研究TDMA下WSN網(wǎng)絡(luò)廣播調(diào)度問(wèn)題（broadcast scheduling problem,BSP）,，期望能實(shí)現(xiàn)在網(wǎng)絡(luò)拓?fù)浞€(wěn)定下,，節(jié)點(diǎn)間消息無(wú)沖突傳輸，并最大化信道利用率．

2  廣播調(diào)度問(wèn)題

      記WSN網(wǎng)絡(luò)為無(wú)向簡(jiǎn)單圖G＝（V,E）,頂點(diǎn)V＝｛v_i｝代表網(wǎng)絡(luò)中傳感節(jié)點(diǎn),，邊E＝｛e_ij｝為節(jié)點(diǎn)問(wèn)傳輸鏈路．若傳感節(jié)點(diǎn)i∈V,，j∈V，且i,j在彼此的傳感半徑內(nèi),，則稱i,j為一跳相鄰節(jié)點(diǎn),，即存在無(wú)線鏈路eij∈E,；若i，j間不存在一跳相鄰節(jié)點(diǎn),，但存在中間節(jié)點(diǎn)k使得e_ik∈E且e_kj∈E,，則稱節(jié)點(diǎn)i，j為二跳相鄰節(jié)點(diǎn)．傳感節(jié)點(diǎn)問(wèn)要能正確收發(fā)數(shù)據(jù),，必須滿足以下約束條件[3]:1）節(jié)點(diǎn)不能同時(shí)接收與發(fā)送數(shù)據(jù),，即若e_ij∈E，則節(jié)點(diǎn)i與節(jié)點(diǎn)j必須分配以不同時(shí)隙來(lái)傳輸數(shù)據(jù),，稱作第1類(lèi)約束,；2）節(jié)點(diǎn)不能同時(shí)接收兩個(gè)或多個(gè)相鄰節(jié)點(diǎn)發(fā)送的數(shù)據(jù)，即若e_j∈且e_kj∈E,，則節(jié)點(diǎn)i,k必須在不同時(shí)隙發(fā)送數(shù)據(jù)以避免在節(jié)點(diǎn)j處發(fā)生沖突,，稱作第2類(lèi)約束．定義二進(jìn)制矩陣S＝｛sij｝表示一個(gè)傳輸調(diào)度，ρ為WSN的帶寬利用率,，用S′＝｛S¹,，S²，…｝表示無(wú)干擾可行調(diào)度集,，則最優(yōu)調(diào)度問(wèn)題描述如下:

      對(duì)于給定拓?fù)鋀SN網(wǎng)絡(luò),，尋找最優(yōu)調(diào)度S^opt∈S′,在滿足第l類(lèi)和第2類(lèi)約束條件下，具有最短的幀長(zhǎng)度S^opt和最大的信道帶寬利用率ρ^opt．

3  基于神經(jīng)網(wǎng)絡(luò)的兩階段調(diào)度方法

3.1  階段

      對(duì)給定拓?fù)涞臒o(wú)向圖,，階段一目標(biāo)是使幀時(shí)隙長(zhǎng)度降為最短,，即用最少時(shí)隙數(shù)M完成調(diào)度．圖的頂點(diǎn)著色問(wèn)題（VCP）求解是NP完全的，目前的求解方法主要是啟發(fā)式算法．雖然順序著色只能找到次優(yōu)解,但其復(fù)雜度最小,。計(jì)算量比其他最優(yōu)和次優(yōu)算法要低1～2個(gè)數(shù)量級(jí)．考慮到傳感節(jié)點(diǎn)的能量和計(jì)算能力有限,，這里結(jié)合最大飽和度與最大度數(shù)準(zhǔn)則設(shè)計(jì)新的頂點(diǎn)著色算法．

      算法包含如下3個(gè)處理環(huán)節(jié)：1）確定幀時(shí)隙長(zhǎng)度上下界．對(duì)于有N個(gè)結(jié)點(diǎn)WSN網(wǎng)絡(luò)，最優(yōu)幀長(zhǎng)度范圍為L(zhǎng)m≤M≤N,，其中Lm＝maxdegi＋1,degi為節(jié)點(diǎn)i的度數(shù),；2）執(zhí)行初始化時(shí)隙分配．令待初始化節(jié)點(diǎn)集合為G＝｛n_i,i=1,2,…,L_m｝,G由圖中具有最大度數(shù)的節(jié)點(diǎn)n₁及與n₁相距l(xiāng)跳節(jié)點(diǎn)的相鄰節(jié)點(diǎn)n_i構(gòu)成，將時(shí)隙i分配給節(jié)點(diǎn)n_i,；3）改進(jìn)的順序著色算法．

      算法

      輸入：原始WSN拓?fù)銰＝（V,E）.

      輸出：節(jié)點(diǎn)時(shí)隙調(diào)度矩陣S=｛S_ij｝_N×M.

      Step1  網(wǎng)絡(luò)節(jié)點(diǎn)拓?fù)渑判颍畬?duì)節(jié)點(diǎn)按照度數(shù)遞減規(guī)律排序并存儲(chǔ)為隊(duì)列Q=｛ni,i＝1,2,…,，N｝，得到網(wǎng)絡(luò)節(jié)點(diǎn)的最大度數(shù)△G,；

      Step2  確定時(shí)隙下確界．置初始時(shí)隙數(shù)M＝△G十1,，調(diào)度矩陣S＝｛0｝_N×M；

      Step3  節(jié)點(diǎn)時(shí)隙初始化調(diào)度．不失一般性,，將第i個(gè)時(shí)隙分配到節(jié)點(diǎn)n_i,，得已調(diào)度節(jié)點(diǎn)集Gc＝｛n_i,i＝1,2,…，M｝,令S_ii=1,計(jì)數(shù)器P＝M＋1,；

      Step4  對(duì)未調(diào)度節(jié)點(diǎn)排序．按照最大飽和度準(zhǔn)則對(duì)剩下的N-L_m個(gè)頂點(diǎn)排序,，存儲(chǔ)為隊(duì)列
 

Q′＝｛n_j,j=L_m+1,…,N｝,；

      Step5  調(diào)度Q′中節(jié)點(diǎn)n_j．搜索滿足2跳內(nèi)約束的時(shí)隙，記不同時(shí)隙數(shù)為Nc,，依據(jù)Nc值分別執(zhí)行以下處理：

      ①若N_c＞1,將第一個(gè)可用時(shí)隙指派給節(jié)點(diǎn)n_j,，Sij=1；

      ②若N_c＝1,將該唯一時(shí)隙指派給節(jié)點(diǎn)n_j,，S_ij=1,；

      ③若N_c＝0,則此時(shí)無(wú)空閑時(shí)隙指派給節(jié)點(diǎn)n_j，轉(zhuǎn)Step7,；

      Step6  判斷是否所有節(jié)點(diǎn)已完成調(diào)度．若P＝N,，算法停止；否則令P=P＋1,，轉(zhuǎn)Step5,；

      Step7  新增一個(gè)時(shí)隙，重新調(diào)度．令M＝M＋1,，轉(zhuǎn)Step5．

      算法Step1排序的計(jì)算量為O（|N|）,Step4排序的計(jì)算量為O（|N-Lm|³）,N為網(wǎng)絡(luò)頂點(diǎn)數(shù),，Lm是頂點(diǎn)最大度數(shù)加1,整個(gè)算法的計(jì)算量約為O（|N|³）

3.2  階段二

      在階段二，使用模糊Hopfield神經(jīng)網(wǎng)絡(luò)對(duì)WSN網(wǎng)絡(luò)節(jié)點(diǎn)進(jìn)行模糊聚類(lèi)^[4,、5] ,，分類(lèi)數(shù)為階段一中求得的M，輸入樣本為待調(diào)度節(jié)點(diǎn)．同一類(lèi)中的所有節(jié)點(diǎn)可以在同一個(gè)時(shí)隙同時(shí)被調(diào)度,；不同類(lèi)中的節(jié)點(diǎn)必須在不同時(shí)隙被調(diào)度．考慮N×M結(jié)構(gòu) Hopfield網(wǎng)絡(luò)，節(jié)點(diǎn)i是否在第j個(gè)時(shí)隙傳輸數(shù)據(jù)由Hopfield處在（i,j）位置神經(jīng)元的輸出Pij確定．利用第2節(jié)中的約束條件來(lái)設(shè)計(jì)優(yōu)化目標(biāo),，即Hopfield網(wǎng)絡(luò)能量函數(shù)E．首先,，所有的數(shù)據(jù)包應(yīng)該在一個(gè)時(shí)隙內(nèi)同步傳送；其次,，當(dāng)節(jié)點(diǎn)i時(shí)隙j傳輸數(shù)據(jù)時(shí),，其他所有節(jié)點(diǎn)i的相鄰節(jié)點(diǎn)不能分配在時(shí)隙j；最后,，當(dāng)節(jié)點(diǎn)i傳輸數(shù)據(jù)時(shí),，i的二跳相鄰節(jié)點(diǎn)也不能被分配到時(shí)隙j去傳輸數(shù)據(jù)．能量函數(shù)E大小反映網(wǎng)絡(luò)當(dāng)前時(shí)隙調(diào)度與最優(yōu)調(diào)度間差距，在考慮所有以上約束條件后,，本文所設(shè)計(jì)能量函數(shù)E如下：
 

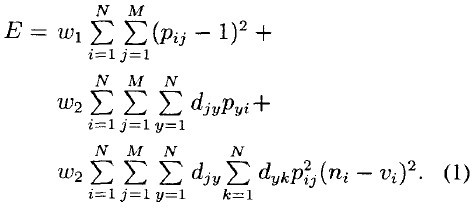
      其中：n_i表示第i個(gè)節(jié)點(diǎn),，d_ij為節(jié)點(diǎn)i，j間歐氏距離,，權(quán)值w₁和w₂為正且滿足w1+w2＝l,權(quán)系數(shù)取值會(huì)影響網(wǎng)絡(luò)收斂性,，需合理選取．V_i為第i類(lèi)歐氏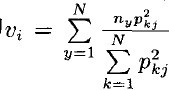中心,，即．（i,j）位置神經(jīng)元輸入為I_ij＝（n_i-v_i）²＋△I_ij,，神經(jīng)元輸出為P_ij,，外部激勵(lì)項(xiàng)△I_ij取常數(shù)．Hopfield網(wǎng)絡(luò)優(yōu)化流程如下：

      Step1  初始化網(wǎng)絡(luò)內(nèi)神經(jīng)元（i,j）輸出P_ij:
 

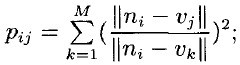
      Step2  更新模糊隸屬度函數(shù)，重新計(jì)算類(lèi)中心v_i,；

      Step3  由式（1）計(jì)算能量函數(shù),；

      Step4  判斷網(wǎng)絡(luò)是否收斂于穩(wěn)定狀態(tài)，若|E（n+1）-E（n）|〉ε（ε為閾值）,，轉(zhuǎn)Step2,；否則，網(wǎng)絡(luò)收斂,，算法終止．

4  實(shí)驗(yàn)結(jié)果與分析

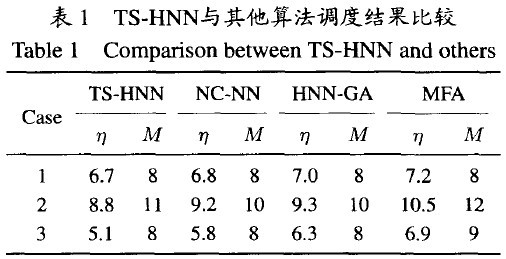
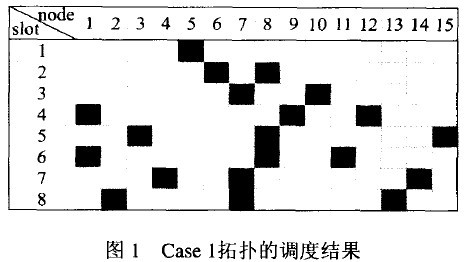
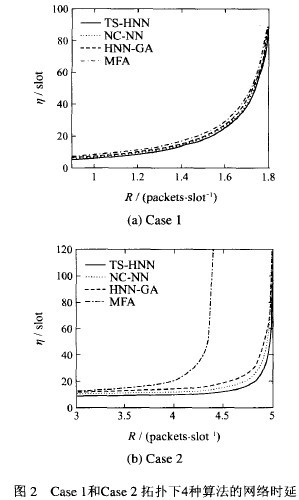
      對(duì)TS-HNN算法的調(diào)度性能進(jìn)行分析,，與平均退火策略（MFA） ^[2] 、基于遺傳算法的Hopfield神經(jīng)網(wǎng)絡(luò)（HNN-GA） [^4]和含噪混沌神經(jīng)網(wǎng)絡(luò)（NC-NN） ^[5]3種方法調(diào)度性能比較．使用3種不同拓?fù)涞臏y(cè)試網(wǎng)絡(luò)Case 1～3^[6] . 實(shí)驗(yàn)中使用的數(shù)據(jù)包為固定長(zhǎng)度,，時(shí)隙長(zhǎng)度設(shè)置為每包所需傳輸時(shí)間,；節(jié)點(diǎn)問(wèn)以泊松分布隨機(jī)收發(fā)數(shù)據(jù)包．每種拓?fù)浣Y(jié)構(gòu)運(yùn)行50次，取平均值進(jìn)行比較．表1給出本文算法（TS-HNN）與其他3種方法求解得到的網(wǎng)絡(luò)最小延遲η和幀長(zhǎng)度M．在節(jié)點(diǎn)數(shù)較少（Case 1）或平均度數(shù)不高時(shí)（Case 3）,，4種算法都能找到最優(yōu)幀長(zhǎng)M＝8,；對(duì)于節(jié)點(diǎn)數(shù)較多具有復(fù)雜結(jié)構(gòu)網(wǎng)絡(luò)（Case 2），TS-HNN也能找到次優(yōu)幀長(zhǎng),；且TS-HNN在3種拓?fù)湎露季哂凶畹偷?a class="innerlink" href="http://forexkbc.com/tags/網(wǎng)絡(luò)時(shí)延" title="網(wǎng)絡(luò)時(shí)延" target="_blank">網(wǎng)絡(luò)時(shí)延．測(cè)試拓?fù)銫ase 1調(diào)度結(jié)果如圖l所示,，填充有黑色的方格代表所在節(jié)點(diǎn)（node）在該時(shí)隙（slot）可被調(diào)度．圖2詳細(xì)描述了網(wǎng)絡(luò)時(shí)延隨數(shù)據(jù)包（packets）服務(wù)速率變化的情況．隨著服務(wù)速率增加，網(wǎng)絡(luò)時(shí)延也在變長(zhǎng),，在節(jié)點(diǎn)數(shù)較少時(shí)（Case 1）,，4種算法的時(shí)延相差不大，如圖 2（a）,；當(dāng)節(jié)點(diǎn)數(shù)增加時(shí)（Case 2）,4種算法下的網(wǎng)絡(luò)時(shí)延差異明顯增大,，如圖2（b）．
 

5  結(jié)束語(yǔ)

      調(diào)度是一類(lèi)經(jīng)典的帶約束資源優(yōu)化分配問(wèn)題本文以傳感器網(wǎng)絡(luò)為研究背景，提出了一種基于圖著色與神經(jīng)網(wǎng)絡(luò)的兩階段廣播調(diào)度算法．算法的基本思想是將廣播調(diào)度問(wèn)題求解轉(zhuǎn)化為兩階段目標(biāo)尋優(yōu)：第1階段借助頂點(diǎn)著色思想搜索給定拓?fù)鋀SN的具有最短時(shí)隙數(shù)目的幀結(jié)構(gòu),；第2階段在上述幀結(jié)構(gòu)下使用模糊Hopfield網(wǎng)絡(luò)為每個(gè)節(jié)點(diǎn)增添額外的無(wú)沖突傳輸時(shí)隙,，從而使得在原有幀長(zhǎng)度下盡可能多的讓更多節(jié)點(diǎn)實(shí)現(xiàn)并行無(wú)干擾傳輸，以最大化信道利用率,，仿真實(shí)驗(yàn)證明了所提方法的有效性．

參考文獻(xiàn)：

[1]PENG Y,SOONG B H,WANG L.Broadcast scheduling in packet radio networks using mixed tabu- greedy algorithm[J].Electronics letters,2004,40（6）:375-376.

[2]WANG G,ARISARIN.Optimal broadcast scheduling in packet radio networks using mean gield annealing[J].IEEE Journal on Selected Areas in Communications.1997,15（2）:250-260.

[3]YEO J,LEE H.An efficient broadcast scheduling algorithm for tdmad- hoc networks[J].Computer Operations Research,2002,29（13）:1793-1806.