??? 設(shè)將d維數(shù)據(jù)集X＝{x_i|x_i∈R^d,，i=1，2,，……,，n}聚集成k個(gè)簇w₁,，w₂，……,，w_k,，它們的質(zhì)心依次為c₁，c₂,，……c_k,，其中n_i是簇w_i中數(shù)據(jù)點(diǎn)的個(gè)數(shù)。采用誤差平方和準(zhǔn)則函數(shù)作為目標(biāo)函數(shù)來(lái)顯式地判斷算法是否結(jié)束,，如公式(1),。利用誤差平方和準(zhǔn)則函數(shù)能把真正屬于同一類的樣本聚合成一個(gè)類型的子集，而把不同類的樣本分開(kāi)^[5],。
???
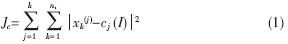
??? 當(dāng)準(zhǔn)則函數(shù)Jc收斂后,，算法結(jié)束。k-means算法步驟描述如下(稱為k-means_1)：
??? (1)給定大小為n的數(shù)據(jù)集X,，令I(lǐng)=1,，選取k個(gè)初始聚類中心c_j(I)，j=1,，2,，3，……,，k,。
??? (2)以c_j(I)為參照點(diǎn)對(duì)X進(jìn)行劃分，計(jì)算每個(gè)樣本數(shù)據(jù)對(duì)象與聚類中心的距離,。若d(x_i,，c_k(I))=min{d(x_i，c_j(I)),，i=1,，2，……n},，其中j=1,，2，……,，k,，i=1，2,，……n,，則將x_i劃分到簇w_k。
??? (3)令I(lǐng)=I+1,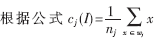，計(jì)算新的聚類中心和誤差平方和準(zhǔn)則函數(shù)的值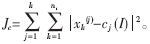
??? (4)若|J_c(I+1)c(I)|<ξ成立,，則算法結(jié)束,。否則，令I(lǐng)=I+1,，返回(2)執(zhí)行,。
2.2 改進(jìn)的k-means算法
??? 在上述k-means算法中，一次迭代內(nèi)把每一個(gè)數(shù)據(jù)對(duì)象分到離它最近的聚類中心所在類,，這個(gè)過(guò)程的時(shí)間復(fù)雜度為O(nkd),。n指的是總的數(shù)據(jù)對(duì)象的個(gè)數(shù)，k是指定的聚類數(shù),，d是數(shù)據(jù)對(duì)象的維數(shù),。新的分類產(chǎn)生以后需要計(jì)算新的聚類中心，這個(gè)過(guò)程的時(shí)間復(fù)雜度為O(nd),。因此,，這個(gè)算法一次迭代需要的總時(shí)間復(fù)雜度為O(nkd)。如果數(shù)據(jù)量比較大,，算法的時(shí)間開(kāi)銷也是相當(dāng)可觀的^[6]。
??? 針對(duì)處理大數(shù)據(jù)量時(shí)開(kāi)支大的不足,，本文提出了一種借用三角形三邊不等定律的思想,，即三角形兩邊之和大于第三邊的定律，減少每次迭代的計(jì)算次數(shù)的改進(jìn)k-means算法,。
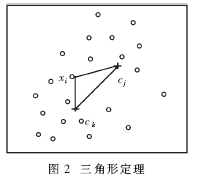??? 在k-means算法的第一個(gè)循環(huán)階段,，每次迭代中要計(jì)算每一個(gè)樣本數(shù)據(jù)到各個(gè)聚類中心的距離，依次比較得到與之距離最小的一個(gè)類中心,，并被分配到這個(gè)類中,。如果能找到一個(gè)方法，避免一些不必要的比較和距離計(jì)算,，就能節(jié)省運(yùn)行的時(shí)間開(kāi)支,。在k-means算法中采用的是歐幾里德距離，因此可以考慮借用幾何三角形中三邊關(guān)系定理：兩邊之和大于第三邊,，從而簡(jiǎn)化計(jì)算比較過(guò)程,。
??? 令x_i∈X，d(c_k,，c_j)為二個(gè)聚類中心的距離,，d(c_k，c_j),、d(x_i,，c_k)與d(x_i，c_j)三邊構(gòu)成了一個(gè)如圖2所示的三角形,。
??? 則有d(c_k,，c_j)≤d(x_i,，c_k)+d(x_i，c_j)
??? 即：d(c_k,，c_j)－d(x_i,，c_k)≤d(x_i，c_j)
??? 如果d(c_k,，c_j)≥2d(x_i,，c_k)，則有：d(x_i,，c_k)≤d(x_i,，c_j)，即x_i到中心c_j的距離比到c_k的距離大,。因此在d(c_k,，c_j)≥2d(x_i，c_k)的前提下,，就不必計(jì)算d(x_i,，c_j)了。k-means算法的演變?nèi)缦滤?稱為k-means_2)：
??? (1)給定大小為n的數(shù)據(jù)集X,，令I(lǐng)=1,，選取k個(gè)初始聚類中心c_j(I)，j=1,，2,，3，……,，k,。
??? (2)計(jì)算每?jī)蓚€(gè)聚類中心間的距離d(c_i(I),c_j(I))，其中i=1,，2,，……，k,，j=1,，2，……,，k,。
??? (3)設(shè)x_i當(dāng)前所在類為w_m，計(jì)算x_i與w_m類中心的距離d(x_i,，c_m(I)),，若d(c_m(I),c_j(I))≥2d((x_i，c_m(I))不成立,，則計(jì)算d(x_i,，c_j(I)),；若d(x_i,c_j(I))＜d(x_i，c_m(I)),，則暫時(shí)將x_i分配到w_j,，返回(3)循環(huán)運(yùn)行，最終將x_i劃分到簇w_m中,。其中j=1,，2，……,，k,，i=1，2,，……n,，m=1，2,，……n,。
??? (4)令I(lǐng)=I+1，計(jì)算新的聚類中心和誤差平方和準(zhǔn)則函數(shù)的值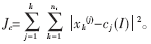
??? (5)若|J_c(I+1)c(I)|<ξ成立,，則算法結(jié)束,。否則，令I(lǐng)=I+1,，返回(2)執(zhí)行。
??? 這里對(duì)算法k-means_1和k-means_2作一個(gè)比較,。在第二個(gè)循環(huán)階段重新計(jì)算聚類中心時(shí),，這二個(gè)算法的時(shí)間復(fù)雜度是相同的。但是在第一個(gè)循環(huán)階段指定聚類簇時(shí),，改進(jìn)的k-means_2算法顯然減少了計(jì)算量,。先考慮一個(gè)樣本點(diǎn)的情況。在k-means_1算法中,，計(jì)算樣本點(diǎn)到各中心點(diǎn)的距離的次數(shù)是k次,，而k-means_2算法中，在最好情況下計(jì)算樣本點(diǎn)到各中心點(diǎn)的距離的次數(shù)是1次,，最壞情況下計(jì)算樣本點(diǎn)到各中心點(diǎn)的距離的次數(shù)是k次,。假設(shè)α為第一循環(huán)階段一次迭代時(shí)一個(gè)樣本點(diǎn)的平均計(jì)算次數(shù)，則有α3? 客戶細(xì)分的實(shí)現(xiàn)
??? 如上所述，本文采用改進(jìn)的k-means算法對(duì)某酒店的現(xiàn)有客戶群進(jìn)行細(xì)分,，建立了RFM模型,。根據(jù)酒店用戶的要求，分別把R,、F,、M三個(gè)要素劃分為3個(gè)等級(jí)，結(jié)合這三個(gè)指標(biāo),，可以把客戶分成9個(gè)等級(jí),，也就是聚類成9個(gè)簇。
??? 實(shí)現(xiàn)聚類算法的主要數(shù)據(jù)結(jié)構(gòu)如下：
??? (1)記錄一個(gè)簇的信息
??? Public Structure clusterlist
??? ??Dim Mean As Double′簇均值
??? ??Dim ClusterNum As Integer′簇中記錄數(shù)
??? ??Dim CluserId As Integer′簇號(hào)
??? ??Dim SquareError As Double′簇中平方誤差和
??? End Structure
??? (2)記錄一個(gè)簇中所有記錄的關(guān)鍵字
??? Public Structure recordnum
??? ??Dim culsterid As Integer ′簇號(hào)
??? ??Dim recordid As ArrayList ′記錄關(guān)鍵字
??? End Structure
??? (3)記錄各個(gè)聚類中心間的距離
??? Dim mean_dist(,，)as double ′用二維數(shù)組記錄中心間的兩兩距離
??? 實(shí)現(xiàn)聚類算法的主要函數(shù)有：
??? (1)init_mean( )：設(shè)定初始聚類中心,。
??? (2)calc_mean_eucli( )：計(jì)算各中心間的歐幾里德距離。
??? (3)calc_sam_eucli( )：計(jì)算各個(gè)樣本點(diǎn)到中心歐幾里德距離,。
??? (4)calc_euclidean( )：計(jì)算二個(gè)點(diǎn)間的歐幾里德距離公式,。
??? (5)find_cluster( )：找到離樣本點(diǎn)最近距離的簇,并分配樣本點(diǎn)到該簇。
??? (6)calc_new_mean( )：一次劃分后計(jì)算新的聚類中心,。
??? (7)calc_Jc( )：計(jì)算誤差平方和準(zhǔn)則函數(shù),。
??? (8)kmeans( )：運(yùn)行k-means算法，若不滿足算法結(jié)束條件則遞歸調(diào)用,。
??? (9)show_cluster( )：展示一個(gè)簇內(nèi)的客戶數(shù)據(jù),。
??? 聚類算法實(shí)現(xiàn)界面如圖3所示，用戶首先要輸入允許的誤差準(zhǔn)則和聚類要生成的簇?cái)?shù),。

?