文獻(xiàn)標(biāo)識碼: A
文章編號: 0258-7998(2012)02-0101-04
近年,盲信號分離BSS(Blind Source Separation)的研究已經(jīng)成為信號處理領(lǐng)域的一個研究熱點(diǎn),涌現(xiàn)出許多盲分離的算法。盲信號分離是在源信號和傳輸信道參數(shù)未知的情況下,僅根據(jù)源信號的統(tǒng)計特性,從觀測信號中分離源信號的過程[1]。盲信號分離所研究的混疊模型主要分為瞬時混疊和卷積混疊兩類。瞬時盲分離已經(jīng)得到廣泛而成熟的研究,聯(lián)合塊(JBD)對角化是解決瞬時盲分離的有效方法[2-4]。然而,傳感器接收到的信號通常是源信號與多徑傳輸信道的卷積混疊信號,這使得卷積盲分離受到越來越多的關(guān)注[5-7]。
與瞬時混疊模型相比,卷積混疊信號模型及其求解更為復(fù)雜。在現(xiàn)有方法中,基于高階統(tǒng)計量的時域算法[8-9]是解卷積混疊盲信號分離問題的一類直觀且有效的方法。作為時域算法,它不需要解決頻域算法[10-11]中所固有的又不得不解決的尺度模糊和排列模糊問題;同時,對一組高階累積量矩陣同時進(jìn)行JBD又可以有效地抑制高斯噪聲的影響。鑒于這兩點(diǎn),本文提出一種基于高階累積量的JBD時域算法,來解決卷積混疊盲信號分離問題。
1 問題描述
盲信號分離的目的是把通過一未知混合系統(tǒng)后的觀測信號分離開來。在卷積混合情況下,假設(shè)源信號通過一個線性有限脈沖響應(yīng)FIR濾波器,也就是說觀測信號是由它們的延遲所組成的線性組合,即:



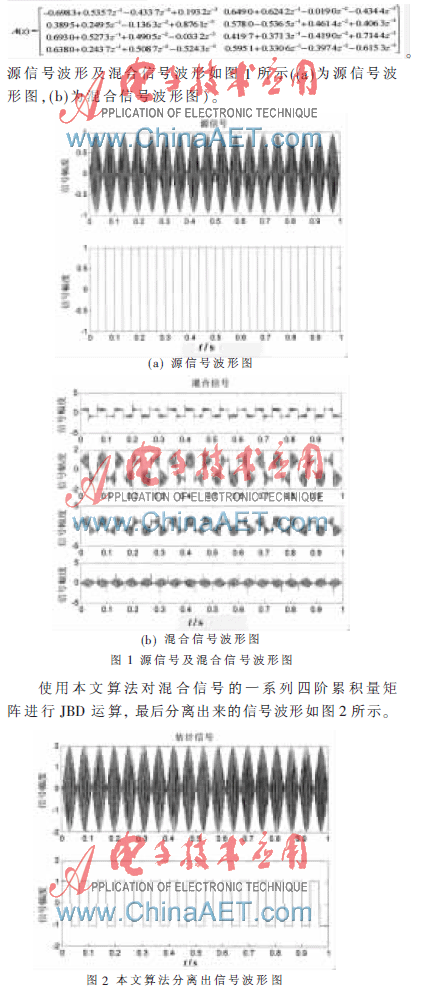
用參考文獻(xiàn)[14]中所提到的自然梯度算法來分離卷積混合的源信號,最后分離出來的信號波形如圖3所示。
從兩種算法分離出的信號波形圖中很難明顯看出其性能的差別,下面通過兩個性能指標(biāo)來客觀地分析一

陣。在此基礎(chǔ)上通過使代價函數(shù)最小化的方法來使累積量矩陣成為塊對角矩陣,進(jìn)而實(shí)現(xiàn)盲分離。計算機(jī)仿真結(jié)果表明,本文算法與自然梯度算法相比有分離精度高及分離速度快的特點(diǎn)。
參考文獻(xiàn)
[1] HAYKIN S. Unsupervised adaptive filtering, vol I: Blind source separation[M]. New York: Wiley Press, 2000:21-23.
[2] SIDIROPOULOS N D, BRO R, GIANNAKIS G B. Parallel factor analysis in sensor array processing[J]. IEEE Trans Signal Process, 2000,48(8):2377-2388.
[3] VANDER V A J. Joint diagonalization via subspace fitting techniques[A].In Proc.ICASSP’01[C]. Piscataway,NJ:IEEE Press, 2001:2773-2776.
[4] ARIE Y. Non-orthogonal joint diagonalization in the leastsquares sensewith application in blind source[J]. IEEE Trans Signal Process, 2002, 50(7):1545-1553.
[5] ABED-MERIAM K, BELOUCHRANI A. Algorithms for joint block diagonaliztion[A]. In Proc. EUSIPCO’04[C]. Vienna:EURASIP Press,2004:209-212.
[6] FEVOTTE C, THEIS F J. Orthonormal approximate joint block diagonalization[R].Technical Report GET/Télécom Pairs, 2007D007, 2007.
[7] 胡可,汪增福.一種基于時頻分析的語音卷積信號盲分離算法[J].電子學(xué)報,2006,34(7):1246-1254.
[8] BUCHNER H, AICHNER R, KELLERMANN W. A generalization of blind source separation algorithms for convolutive mixtures based on second-order statistics[J]. IEEE Transactions on Speech and Audio Processing, 2005,13(1):120-134.
[9] GHENNIOUI H, FADAILI E M, MOREAU N T, et al. A nonunitary joint block diagonalization algorithm for blind separation of convolutive mixtures of sources[J]. IEEE Signal Processing Letters, 2007,14(11): 860-863.
[10] SAWADA H, MUKAI R, ARAKI S, et al. A robust and precise method for solving the permutation problem of frequency-domain blind source separation[J]. IEEE Transactions on Speech and Audio Processing, 2004,12(5): 530-538.
[11] HE Z S, XIE S L, DING S X, et al. Convolutive blind source separation in the frequency domain based on sparse representation[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007,15(5):1551-1563.
[12] GOROKHOV A, LOUBATON P. Subspace based techniques for second order blind separation of convolutive mixtures with temporally correlated sources [J]. IEEE Trans.Circuit Syst., 1997,44(9):813-820.
[13] BOUSBIAH-SALAH H, BELOUCHRANI A,ABED-MERAM K. Jacobi-like algorithm for blind signal separation of convolutive mixtures[J]. Electron. Lett.,2001(37):1049-1050.
[14] AMARI S, DOUGLAS S, CICHOCKI A,et al. Multichannel blind deconvolution and equalization using the natural gradient[J]. In Proc. 1st IEEE Workshop Signal Processing Advanced Wireless Commun., Paris, France, 1997(4):101-104.

