關(guān)鍵詞: 智能混合系統(tǒng) 自然智能 神經(jīng)網(wǎng)絡(luò) 專家系統(tǒng) 模糊邏輯
人工智能的核心任務(wù)是模擬自然智能。而自然智能表現(xiàn)在不同的層次和不同的方面,因此仿智的方法有多種,如模擬抽象思維層次的符號(hào)主義,模擬形象思維層次的聯(lián)接主義,模擬智能行為層次的行為主義等。雖然各種智能信息處理方法與概念都已提出,并取得不少成果,但相關(guān)的研究工作還處在較低的水平,在單獨(dú)模擬人類智能活動(dòng)時(shí),尚存在各種局限性。生物物理、心理認(rèn)知學(xué)的研究表明,智能信息處理能力是包括上述各種智能處理能力的綜合集成。可以相信,今后智能本質(zhì)和智能綜合集成方面的系統(tǒng)研究將是非常重要的研究領(lǐng)域。
盡管自然智能覆蓋面廣,但人是萬物之靈,應(yīng)將對(duì)人的智能的研究作為重點(diǎn),并輔以對(duì)其他自然智能的研究,從而最終解開智能的奧秘。同時(shí),在研究智能綜合集成方面,由于抽象思維和形象思維是人類最主要的二種思維形式,并且符號(hào)主義和聯(lián)接主義學(xué)派的方法和理論較為充實(shí),因此,應(yīng)重點(diǎn)進(jìn)行上述二者的集成研究,然后將其原理和方法推廣到其他廣義人工智能的綜合集成中。
1 四類典型的智能混合系統(tǒng)
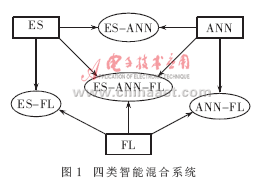
智能混合系統(tǒng)主要涉及專家系統(tǒng)(Expert System,ES)、神經(jīng)網(wǎng)絡(luò)(Artificial Neural Network,ANN)和模糊邏輯(Fuzzy Logic,F(xiàn)L)三種技術(shù)。神經(jīng)網(wǎng)絡(luò)易于表達(dá)感性知識(shí),專家系統(tǒng)易于表達(dá)理性知識(shí),而理性知識(shí)中又含有大量的模糊知識(shí),因此需要使用模糊邏輯來描述。于是,不同技術(shù)的組合,便構(gòu)成了不同類型的智能混合系統(tǒng),主要有四種(如圖1所示)。
1.1 神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)結(jié)合
神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)主要有三種結(jié)合方式,下面分別予以介紹。
(1)基于神經(jīng)網(wǎng)絡(luò)的專家系統(tǒng)
這類系統(tǒng)又稱聯(lián)接專家系統(tǒng),其全部或部分功能由神經(jīng)網(wǎng)絡(luò)實(shí)現(xiàn),實(shí)現(xiàn)方式有兩種。
①從神經(jīng)網(wǎng)絡(luò)中抽取規(guī)則構(gòu)造專家系統(tǒng)
這種方式希望將神經(jīng)網(wǎng)絡(luò)的隱式“黑箱”知識(shí)表示為顯式規(guī)則形式,并用于推理或解釋神經(jīng)網(wǎng)絡(luò)的行為。在訓(xùn)練前不需要了解領(lǐng)域知識(shí)的結(jié)構(gòu),也不需要將領(lǐng)域知識(shí)的結(jié)構(gòu)強(qiáng)加于神經(jīng)網(wǎng)絡(luò),關(guān)鍵是通過神經(jīng)網(wǎng)絡(luò)的自組織、自學(xué)習(xí)來獲得易于人類認(rèn)識(shí)、理解的領(lǐng)域知識(shí)。
②規(guī)則知識(shí)編碼于神經(jīng)網(wǎng)絡(luò)系統(tǒng)
這種方式比較簡(jiǎn)單,實(shí)質(zhì)是利用神經(jīng)網(wǎng)絡(luò)將己有的領(lǐng)域知識(shí)進(jìn)行優(yōu)化求精,所訓(xùn)練的神經(jīng)網(wǎng)絡(luò)在形式上直接對(duì)應(yīng)于專家系統(tǒng)的推理網(wǎng)絡(luò),可以直接用于推理和解釋神經(jīng)網(wǎng)絡(luò)的結(jié)論和行為。
上述兩種方法的區(qū)別在于:前者在對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練之前無需將領(lǐng)域知識(shí)的結(jié)構(gòu)強(qiáng)加于神經(jīng)網(wǎng)絡(luò),所學(xué)得的神經(jīng)網(wǎng)絡(luò)難以進(jìn)行自我解釋,神經(jīng)網(wǎng)絡(luò)中的知識(shí)只有抽取出來并表示為規(guī)則知識(shí)后才成為易于理解的顯式知識(shí);后者在對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練之前需要將領(lǐng)域知識(shí)的結(jié)構(gòu)編碼于神經(jīng)網(wǎng)絡(luò)中,所學(xué)得的神經(jīng)網(wǎng)絡(luò)己將知識(shí)進(jìn)行了顯式表示,因而具有自我解釋能力。
很多學(xué)者進(jìn)行了這方面的研究和開發(fā)工作。Gallant[1]首次提出并建立了聯(lián)接專家系統(tǒng),Caudill[2]提出了建立額外的小型規(guī)則系統(tǒng)用于解釋神經(jīng)網(wǎng)絡(luò)行為的方法等。
這類混合系統(tǒng)優(yōu)勢(shì)在于自學(xué)習(xí)和自適應(yīng)能力,可以有效克服專家系統(tǒng)在知識(shí)獲取方面所遇到的困難,開發(fā)時(shí)間較短;缺點(diǎn)在于對(duì)神經(jīng)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)、非線性活動(dòng)函數(shù)及各種參數(shù)的選擇缺乏系統(tǒng)的指導(dǎo)原則,應(yīng)用領(lǐng)域較窄,其解釋能力方面也有待進(jìn)一步研究。
(2)基于知識(shí)的神經(jīng)網(wǎng)絡(luò)系統(tǒng)
這類系統(tǒng)也稱為專家網(wǎng)絡(luò),是由專家系統(tǒng)作為神經(jīng)模塊構(gòu)成的事件驅(qū)動(dòng)網(wǎng)絡(luò)。在該系統(tǒng)中,神經(jīng)元包括“與”、“或”、“非”等邏輯神經(jīng)元和前提、結(jié)論神經(jīng)元,它們之間的聯(lián)接權(quán)代表專家系統(tǒng)中的確定性因子,故可將專家系統(tǒng)規(guī)則集表達(dá)為專家網(wǎng)絡(luò)。
這方面的研究成果主要有:Kuncicky[3]提出的專家網(wǎng)絡(luò),Towell[4]提出的一種基于知識(shí)的人工神經(jīng)網(wǎng)絡(luò)。可以看出,專家網(wǎng)絡(luò)的缺點(diǎn)是學(xué)習(xí)時(shí)只改變權(quán)值,而不能改變網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu),因而不能向不完全的初始規(guī)則集增加新的符號(hào)規(guī)則。為了使專家系統(tǒng)具備學(xué)習(xí)能力,以期根本解決知識(shí)獲取的瓶頸問題,對(duì)專家系統(tǒng)進(jìn)行合理描述并且開發(fā)有效的學(xué)習(xí)算法將是十分重要的研究方向。
(3)基于神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)的混合系統(tǒng)
這類系統(tǒng)的基本出發(fā)點(diǎn)是將復(fù)雜系統(tǒng)分解成各種功能子系統(tǒng),分別由神經(jīng)網(wǎng)絡(luò)或?qū)<蚁到y(tǒng)實(shí)現(xiàn),研究的主要問題包括混合專家系統(tǒng)的結(jié)構(gòu)框架和選擇實(shí)現(xiàn)功能子系統(tǒng)方式的準(zhǔn)則兩方面的問題。這兩個(gè)問題的研究相輔相成,不可分割。混合方式有兩種:①從應(yīng)用的角度出發(fā),對(duì)易于獲取其產(chǎn)生式規(guī)則的子系統(tǒng)使用專家系統(tǒng)技術(shù),其余的功能由神經(jīng)網(wǎng)絡(luò)來實(shí)現(xiàn),此時(shí)系統(tǒng)的結(jié)構(gòu)由實(shí)際問題來決定。②從功能的角度出發(fā),可以用神經(jīng)網(wǎng)絡(luò)實(shí)現(xiàn)專家系統(tǒng)的規(guī)則推理、知識(shí)獲取等功能,專家系統(tǒng)則負(fù)責(zé)知識(shí)的顯式表示和神經(jīng)網(wǎng)絡(luò)結(jié)論的驗(yàn)證和解釋工作。
基于此,Suddarth[5]提出將復(fù)雜系統(tǒng)分解為功能子系統(tǒng)的混合系統(tǒng)結(jié)構(gòu),Tirri[6]則另辟蹊徑,用神經(jīng)網(wǎng)絡(luò)實(shí)現(xiàn)專家系統(tǒng)規(guī)則集前提條件。
雖然神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)結(jié)合兼有二者之長(zhǎng),但同時(shí)也帶來了單一技術(shù)不曾遇到的問題:①神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)的信息交互問題;②學(xué)習(xí)過程所引發(fā)的系統(tǒng)可信度問題。前者的解決依賴于神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)知識(shí)表示的轉(zhuǎn)換機(jī)制或同時(shí)適合兩者的公共知識(shí)表示體系,后者的解決有賴于不同體制下的知識(shí)的公共表示和統(tǒng)一的參數(shù)學(xué)習(xí)機(jī)制。顯然,解決上述兩個(gè)問題己成為實(shí)現(xiàn)神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)相結(jié)合的當(dāng)務(wù)之急。
1.2 模糊神經(jīng)網(wǎng)絡(luò)
模糊神經(jīng)網(wǎng)絡(luò)(Fuzzy Neural Network,F(xiàn)NN)是模糊理論同神經(jīng)網(wǎng)絡(luò)相結(jié)合的產(chǎn)物。它匯集了神經(jīng)網(wǎng)絡(luò)與模糊理論的優(yōu)點(diǎn),集學(xué)習(xí)、聯(lián)想、識(shí)別、自適應(yīng)及模糊信息處理于一體。近年來,F(xiàn)NN的理論及應(yīng)用得到了飛速發(fā)展,各種新的FNN模型的提出以及與其相適應(yīng)的學(xué)習(xí)算法的研究不僅加速了 FNN理論的完善,而且它們?cè)趯?shí)際中得到了非常廣泛的應(yīng)用。本文以此為基礎(chǔ),進(jìn)一步討論完整意義上的FNN的網(wǎng)絡(luò)模型、學(xué)習(xí)算法、模糊函數(shù)逼近性能和學(xué)習(xí)能力等關(guān)鍵問題,并對(duì)今后的研究提出自己的看法。
(1)FNN模型和算法
目前FNN模型絕大多數(shù)都是多層前向網(wǎng)絡(luò)結(jié)構(gòu),主要區(qū)別在于隸屬度函數(shù)、模糊加權(quán)算子、模糊激勵(lì)函數(shù)和輸入輸出的形式,以及結(jié)構(gòu)與參數(shù)的設(shè)定和調(diào)整方法。
FNN可以分為單純型和混合型兩種:①單純型FNN:輸入輸出和連接權(quán)全部或部分采用模糊實(shí)數(shù),計(jì)算結(jié)點(diǎn)輸出的權(quán)相加采用模糊算術(shù)算子,函數(shù)計(jì)算采用擴(kuò)展原理;②混合型FNN:輸入輸出和連接權(quán)全部或部分采用模糊實(shí)數(shù),計(jì)算結(jié)點(diǎn)輸出的權(quán)相加還采用了除模糊算術(shù)算子以外的模糊邏輯算子,函數(shù)計(jì)算采用擴(kuò)展原理。這兩種模型既可以處理模糊信息,也可以處理非模糊信息,因?yàn)槠胀▽?shí)數(shù)可以作為一種特殊的模糊數(shù)。
這方面成果很多,重要的有:Chen[7]針對(duì)基于模糊訓(xùn)練樣本的模式分類問題提出了多類FNN分類器,模糊自適應(yīng)諧振理論(ART)[8]成功解決了模糊信息的存儲(chǔ)和記憶問題。除此之外,還有不少文獻(xiàn)也都提出了各種各樣的FNN模型和算法,不再贅述。
(2)FNN的函數(shù)逼近問題
已經(jīng)證明普通多層前向NN和模糊系統(tǒng)(輸入輸出均為非模糊數(shù))是連續(xù)函數(shù)逼近器,并且系統(tǒng)之間可以等價(jià)互換,這為在輸入輸出非模糊的環(huán)境下設(shè)計(jì)模糊神經(jīng)網(wǎng)絡(luò)混合系統(tǒng)提供了扎實(shí)的理論基礎(chǔ)。雖然模糊神經(jīng)網(wǎng)絡(luò)系統(tǒng)逼近問題取得了許多理論成果,但是己有結(jié)果僅僅是針對(duì)采用單值模糊產(chǎn)生器的模糊系統(tǒng)得到的,對(duì)于輸入輸出均為模糊數(shù)的FNN函數(shù)逼近問題的研究相對(duì)比較薄弱,而在設(shè)計(jì)FNN的同時(shí)論證設(shè)計(jì)模型的逼近性能有時(shí)非常必要。因此,F(xiàn)NN函數(shù)逼近問題的研究重點(diǎn)是:①尋找能夠作為連續(xù)模糊函數(shù)逼近器的FNN;②給出通用的作為連續(xù)模糊函數(shù)逼近器的FNN的構(gòu)造型定理。
在這方面Buckley[9]做了開創(chuàng)性的工作,定義了模糊函數(shù)、連續(xù)模糊函數(shù)和連續(xù)模糊函數(shù)逼近器等概念,并且證明如果FNN模型是單純型,則它不可能是一個(gè)連續(xù)模糊函數(shù)逼近器;如果FNN模型是混合型,則它可能是一個(gè)連續(xù)模糊函數(shù)逼近器。但是,這不是一個(gè)構(gòu)造型定理,它沒有給出設(shè)計(jì)連續(xù)模糊函數(shù)逼近器的FNN的方法。Feuring[10]在研究FNN的構(gòu)造方面做出了突出貢獻(xiàn),給出了一種連續(xù)模糊函數(shù)逼近器的FNN的構(gòu)造方法。這些結(jié)果對(duì)實(shí)際系統(tǒng)設(shè)計(jì)中模糊函數(shù)的選取具有指導(dǎo)性的意義。
(3)關(guān)于FNN的學(xué)習(xí)能力
FNN的學(xué)習(xí)包括兩個(gè)方面:一是有效的學(xué)習(xí)算法,二是學(xué)習(xí)的精度和普適性。通常,由于模糊運(yùn)算的復(fù)雜性和一些算子的不連續(xù)性,在多層前向NN中常用的BP算法和其他一些優(yōu)化算法不能直接用于多層前向FNN,而修改后的Fuzzy BP規(guī)則解決了此問題。為簡(jiǎn)化學(xué)習(xí)算法,F(xiàn)NN的許多學(xué)習(xí)算法都采用經(jīng)驗(yàn)學(xué)習(xí)公式或規(guī)則,盡管缺乏完備的理論,但效果顯著。
FNN的學(xué)習(xí)精度和函數(shù)逼近性能密切相關(guān)。盡管訓(xùn)練樣本有限,但只要網(wǎng)絡(luò)足夠大,學(xué)習(xí)算法有效,達(dá)到高精度的學(xué)習(xí)目標(biāo)并非難事。然而訓(xùn)練樣本的有限性導(dǎo)致學(xué)習(xí)結(jié)果的普適性變差已成為學(xué)習(xí)的主要矛盾。目前關(guān)于FNN系統(tǒng)的普適性問題成果很少,因此,如何將非模糊學(xué)習(xí)機(jī)的普適性分析方法推廣到模糊學(xué)習(xí)機(jī),成為FNN學(xué)習(xí)問題研究的關(guān)鍵。
盡管這幾年FNN成果不菲,但仍然存在如下問題:
①FNN模型的研究主要是NN的模糊化和FS的神經(jīng)網(wǎng)絡(luò)化,很少從人腦對(duì)模糊信息的處理機(jī)制上考慮問題。應(yīng)從智能問題本身創(chuàng)造性地設(shè)計(jì)FNN模型,體現(xiàn)新的解決智能問題的思想。②FNN的數(shù)值計(jì)算導(dǎo)致嚴(yán)重的計(jì)算量問題。因此,有必要建立語言層次上的計(jì)算理論。③反饋FNN可以有效地解決成組、約束和動(dòng)態(tài)學(xué)習(xí)以及空間關(guān)系學(xué)習(xí)等許多單項(xiàng)FNN很難解決的問題。因此,要加強(qiáng)反饋FNN的研究。
1.3 模糊專家系統(tǒng)
專家系統(tǒng)中模糊性的一個(gè)最主要表現(xiàn)就是模糊概念的存在。很好地表達(dá)模糊概念并不等于問題的根本解決,還要解決其使用問題。也就是在這樣的專家系統(tǒng)中如何進(jìn)行推理。這方面的成果不多,僅集中在專家系統(tǒng)中模糊概念的表達(dá)與推理方法的研究上。
1.4 模糊神經(jīng)網(wǎng)絡(luò)專家系統(tǒng)
專家系統(tǒng)的知識(shí)獲取及經(jīng)驗(yàn)性知識(shí)處理需要融合神經(jīng)網(wǎng)絡(luò)的高質(zhì)量、高效率的學(xué)習(xí)能力與模糊邏輯出色的對(duì)于不完善知識(shí)的描述能力。發(fā)揮各自優(yōu)勢(shì),能明顯提高專家系統(tǒng)的性能。
(1)知識(shí)表示問題
在實(shí)際問題中含有大量的模糊知識(shí),僅用傳統(tǒng)的知識(shí)表示方法是不夠的。因此,模糊規(guī)則和隸屬函數(shù)的引入成為必然。
(2)信念傳播問題
推理期間可能有多條相同結(jié)論的規(guī)則同時(shí)滿足條件,在傳統(tǒng)的專家系統(tǒng)中,總是采用最大優(yōu)先級(jí)規(guī)則,誤差較大。為了解決這個(gè)問題,采用神經(jīng)網(wǎng)絡(luò)進(jìn)行推理,結(jié)論的可信度是各條規(guī)則結(jié)論可信度的組合,權(quán)系數(shù)是通過訓(xùn)練網(wǎng)絡(luò)得到的。
(3)更有效的推理
由于推理是通過神經(jīng)網(wǎng)絡(luò)實(shí)現(xiàn)的,減少了規(guī)則匹配過程,從而加快了推理速度。
(4)學(xué)習(xí)問題
利用神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)能力可容易地求精模糊規(guī)則,從而提高系統(tǒng)的適應(yīng)能力。
Zha[11]提出了一種神經(jīng)模糊專家Petri網(wǎng)模型,Li[12]開發(fā)了一個(gè)混合智能系統(tǒng),還有不少文獻(xiàn)在這方面也作了相應(yīng)的研究工作。
綜上所述,以神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)的結(jié)合、模糊神經(jīng)網(wǎng)絡(luò)、模糊專家系統(tǒng)以及模糊神經(jīng)網(wǎng)絡(luò)專家系統(tǒng)四種類型為主的智能混合系統(tǒng)成果頗多,代表了目前智能混合系統(tǒng)發(fā)展的主流方向。所涉及的技術(shù)主要有專家系統(tǒng)、神經(jīng)網(wǎng)絡(luò)和模糊理論三種。但是智能混合系統(tǒng)絕不僅限于此,還有許多智能技術(shù),如粗糙集、遺傳算法、Petri網(wǎng)等也成為智能混合系統(tǒng)集成技術(shù)的研究熱點(diǎn),不少文獻(xiàn)在這方面做出了突出的貢獻(xiàn)。
2 成果總結(jié)及進(jìn)一步的研究方向
目前,智能混合系統(tǒng)己經(jīng)取得了許多成果,在眾多領(lǐng)域中得到了相當(dāng)成功的應(yīng)用,解決了許多單一智能系統(tǒng)不能解決的復(fù)雜問題,并且正在向著更深的研究層次挺進(jìn)。這些成果集中表現(xiàn)在以下方面。
(1)利用神經(jīng)網(wǎng)絡(luò)優(yōu)良的自組織、自學(xué)習(xí)和自適應(yīng)能力初步解決了專家系統(tǒng)知識(shí)獲取的“瓶頸問題”。
(2)利用專家系統(tǒng)良好的解釋機(jī)能較好地解釋了神經(jīng)網(wǎng)絡(luò)的行為,彌補(bǔ)了神經(jīng)網(wǎng)絡(luò)中知識(shí)表達(dá)的“黑箱結(jié)構(gòu)”。
(3)神經(jīng)網(wǎng)絡(luò)與專家系統(tǒng)混合的系統(tǒng)通過融合模糊邏輯進(jìn)行知識(shí)描述與推理,明顯地改善了專家系統(tǒng)的性能。
盡管智能混合系統(tǒng)的研究取得了許多矚目的成果,但其理論體系還很不完善,需從以下幾個(gè)方面進(jìn)一步深入研究。
(1)立足于廣義人工智能,以模擬自然智能為目的,從思維科學(xué)的角度出發(fā),研究人類認(rèn)知過程中抽象思維與形象思維在功能、知識(shí)表達(dá)、思維活動(dòng)等方面的內(nèi)在關(guān)系。
(2)智能混合系統(tǒng)需要統(tǒng)一的知識(shí)表示方法,需要研究接近于人類思維模式的知識(shí)表示機(jī)理。
(3)利用神經(jīng)網(wǎng)絡(luò)有效地進(jìn)行知識(shí)獲取。
(4)研究實(shí)用的神經(jīng)網(wǎng)絡(luò)推理及結(jié)果解釋方法。
(5)將已取得的智能混合系統(tǒng)研究成果向其他智能形式的綜合集成中推廣,從而進(jìn)行更廣泛的智能系統(tǒng)集成方法研究。
3 結(jié) 論
智能混合系統(tǒng)研究應(yīng)從人類智能行為本質(zhì)入手,著眼于知識(shí)在人腦中表示、存儲(chǔ)及實(shí)現(xiàn)各種人類思維方式的生理基礎(chǔ)。隨著對(duì)人類生物神經(jīng)系統(tǒng)、思維模式的進(jìn)一步認(rèn)識(shí),研究各種新的集成系統(tǒng)模型,實(shí)現(xiàn)大腦思維過程的模擬,進(jìn)而實(shí)現(xiàn)整個(gè)自然智能的模擬,從而最終揭開智能的奧秘。
參考文獻(xiàn)
1 Gallant I S.Connectionist expert systems.Communication of the ACM,1988;31(2):152
2 Caudill M.Using neural nets:Hybrid expert networks.AI Expert,1990;5(11):49
3 Kuncicky D C,Hruska S I,Lacher R C.Hybrid systems:the equivalence of rule-based expert systems and artificial neural network inference.Int.J.of Expert Systems,1991;4(3):281
4 Towell G G,Shavlik J W,Noordewier M O.Refinement of approximate domain theories by knowledge-based neural networks.In:Proc.AAAI-90,August,1990:861
5 Suddarth S C,Holden A D C.Symbolic-neural systems and the use of hints for developing comples systems.Int.J. Pattern Recognition,1991;5(4):503
6 Tirri H.Implementation expert system rule conditions by neural networks.New Generation Comput.,1991;10:55
7 Chen K H.A multiclass neural network classifier with fuzzy teaching inputs.Fuzzy Sets and Systems,1997;91:15
8 Carpenter G A,Grossberg A,Rosen D B.Fuzzy ART fast stable learning and categorization of analog patterns by an adaptive resonance systems.Neural Networks,1991;4:759
9 Buckley J J,Hayashi Y.Fuzzy neural networks:a survey. Fuzzy Sets and Systems,1994;66:1
10 Feuring T,Lippe W.The fuzzy neural network approximation lemma.Fuzzy Sets and Systems,1999;102:227

