《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 嵌入式技術(shù) > 設(shè)計應(yīng)用 > 一種基于小波降噪的GNSS軌跡平滑算法
一種基于小波降噪的GNSS軌跡平滑算法
來源：電子技術(shù)應(yīng)用2012年第5期
李立言,， 趙民建,， 鐘 杰
浙江大學(xué) 信息與電子工程學(xué)系， 浙江 杭州310027
摘要： 當(dāng)載體具有高階動態(tài)時,，基于載波多普勒平滑偽距的解算誤差擴大,，且載體軌跡小波降噪處理結(jié)果會發(fā)生畸變,。針對這些問題,，提出了一種新的基于小波降噪載體位置平滑算法,。算法對基于偽碼測距和載波多普勒平滑偽距的解算結(jié)果進(jìn)行差分，并根據(jù)差分值的頻譜特征,，選擇合適的尺度進(jìn)行小波降噪處理后,與基于載波多普勒平滑偽距的解算結(jié)果求和得到軌跡平滑結(jié)果。仿真結(jié)果表明,，該算法在載體最大加加速度為50 m/s3的條件下,，定位均值偏差小于0.04 m，標(biāo)準(zhǔn)差小于1.3 m,。
中圖分類號： TN961
文獻(xiàn)標(biāo)識碼： A
文章編號： 0258-7998(2012)05-0118-04
A GNSS track smoothing method based on wavelet de-noising
Li Liyan, Zhao Minjian, Zhong Jie
Department of Information Science and Electronic Engineering,，Zhejiang University,， Hangzhou 310027，China
Abstract： When user jerk increases, the estimation errors of both carrier Doppler smoothed pseudoranges based positioning and wavelet de-noising applied directly to track smoothing will become larger. A novel track smoothing method based on wavelet de-noising is proposed in this paper to solve these problems. Differential of the position estimations based on code generated pseudoranges and carrier Doppler smoothed pseudoranges is calculated. After wavelet de-noising of the differential, the sum of the result and the carrier Doppler smoothed pseudoranges based positioning is used as the smoothing result. Simulation result shows that estimation bias of the proposed method is less than 0.04 m and the standard deviation is less than 1.3 m when the user maximum jerk is 50 m/s3.
Key words : high dynamic,； GNSS receiver,； wavelet de-noising； track smoothing

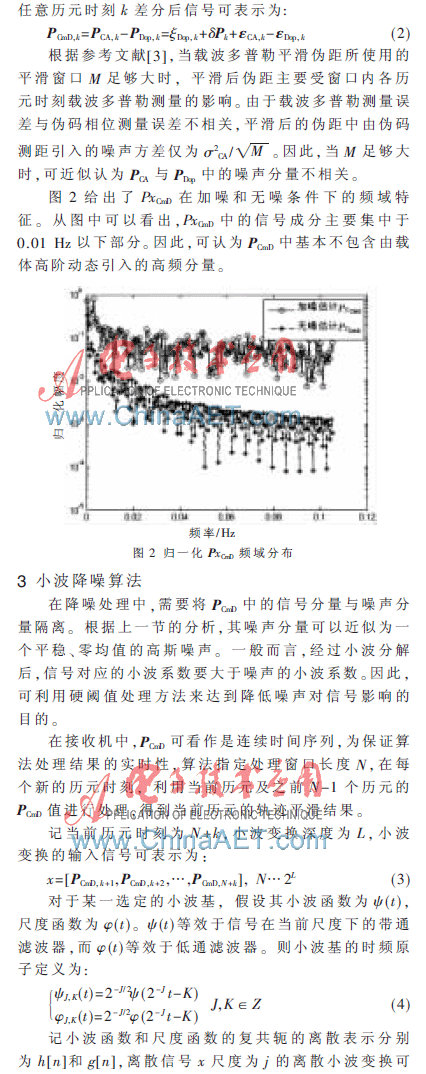
    小波域中各個尺度上信號大部分能量集中在信號突變位置,，而噪聲對應(yīng)的小波系數(shù)在各個尺度上的分布均勻且幅值較小,。參考文獻(xiàn)[1]提出了基于小波系數(shù)閾值的降噪方法。非線性閾值估計器能夠在多種不同類型信號條件下接近最小最大風(fēng)險,，具有比線性估計器更好的性能,。

    在GNSS接收機中，衛(wèi)星信號經(jīng)過偽碼相位估計,、載波頻偏估計及位置解算等處理后得到載體位置,。不同的背景噪聲和不同的信號處理算法都會影響估計誤差特性，因此很難給出通用的載體位置解算誤差模型或其近似描述,。在低動態(tài)GNSS接收機中,為平滑載體運動軌跡,，降低載體位置解算中的噪聲，通常在獲取載體速度估計后,，采用卡爾曼濾波的方式達(dá)到位置平滑的目的[2],。但在高動態(tài)接收機中，載體高階動態(tài)變化會導(dǎo)致對載體速度估計精度的下降,?；谒俣鹊?a class="innerlink" href="http://forexkbc.com/tags/軌跡平滑" title="軌跡平滑" target="_blank">軌跡平滑方法精度隨之降低。同時,，載體高階動態(tài)可能導(dǎo)致載波相位跟蹤環(huán)路的失鎖或周跳,。載波相位測量結(jié)果不能直接用于載體位置解算處理。
    參考文獻(xiàn)[3]提出了一種基于載波多普勒的偽距平滑算法,。算法通過對載波多普勒的數(shù)值積分替代載波相位的直接測量,，實現(xiàn)了載波相位不可用條件下的偽距預(yù)處理。該算法在低動態(tài)條件下具有分米級的定位精度,。但隨載體動態(tài)提高,，數(shù)值積分誤差及環(huán)路頻率跟蹤誤差放大使平滑偽距偏差增加，從而造成解算結(jié)果與真實值的偏差擴大,。
    本文提出了一種新的基于小波降噪載體位置平滑算法,。基于偽碼測距的解算均值偏差較小但誤差方差較大的特征,，對基于載波多普勒平滑偽距的解算結(jié)果進(jìn)行誤差修正,。利用位置差分的方式降低了待處理數(shù)據(jù)中的高頻成分，降低小波降噪處理中的門限，從而提高了算法的噪聲隔離性能,。最后通過采集信號重構(gòu)高動態(tài)場景對算法性能進(jìn)行了仿真驗證,。
1 基于差分信號的軌跡平滑算法
    圖1所示為載體具有加加速度條件下，基于偽碼測距的解算,、基于載波多普勒平滑偽距的解算及基于小波直接軌跡平滑得到的一組位置估計仿真結(jié)果,。仿真中載體從第1 140 s開始進(jìn)行變加速運動，其最大加加速度為50 m/s3,。從圖中可以看出,，基于偽碼測距的解算算法估計誤差方差較大，而后兩種算法在載體具有高階動態(tài)時會發(fā)生誤差擴大的現(xiàn)象,，因此并不適合高動態(tài)條件下的應(yīng)用,。

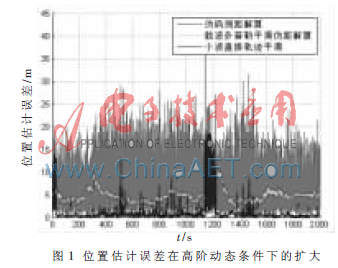
    參考文獻(xiàn)[4]提出的WaveSmoothTM算法通過對偽碼測距與載波相位測距間偏差進(jìn)行小波分析，選取合適的小波變換尺度和數(shù)據(jù)長度對信號進(jìn)行降噪處理,。具有較低的運算開銷和較好的實時性能,，并且比傳統(tǒng)的時域平滑算法和頻域濾波方法能夠更好地濾除偽距測量中的低頻噪聲分量。
    基于類似的想法,，考慮應(yīng)用小波降噪處理構(gòu)成載體軌跡實時平滑算法,。對基于偽碼測距和載波多普勒平滑偽距的解算結(jié)果進(jìn)行差分，以降低數(shù)據(jù)中的高階變化,。對差分結(jié)果進(jìn)行小波降噪處理后,，與基于載波多普勒平滑偽距的解算結(jié)果求和得到軌跡平滑結(jié)果。


 


  
   
    算法平滑后載體位置估計精度如表1所示,?？梢钥闯觯惴ㄔ诟邉討B(tài)條件下載體位置估計誤差均值基本為0,，單軸標(biāo)準(zhǔn)差小于1 m,，接近參考文獻(xiàn)[3]中低動態(tài)條件下載波多普勒平滑偽距定位算法的性能。

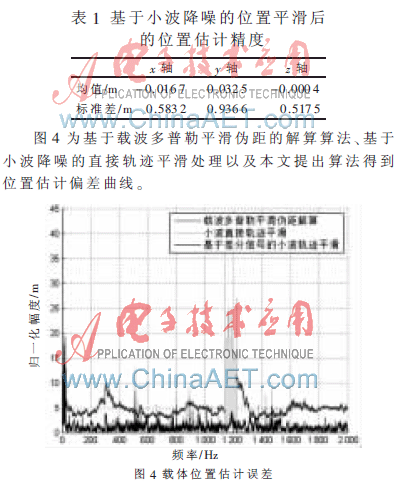
    從圖4中可以看出,，基于小波降噪的直接軌跡平滑處理和本文提出的算法在位置估計均值精度上明顯優(yōu)于基于載波多普勒平滑偽距的解算算法,。在第1 140 s前后，載體以較大加加速度運動時,，受頻率環(huán)穩(wěn)態(tài)跟蹤誤差影響,，載波多普勒平滑偽距定位算法位置估計誤差發(fā)生擴散, 基于載波多普勒平滑偽距的解算算法位置估計誤差逐步放大，直至第1 198 s載體轉(zhuǎn)為勻速運動后誤差逐漸縮小,。而基于差分信號的小波軌跡平滑算法在整個定位過程中基本排除了上述原因引入位置估計誤差,，具有更好的性能。
    在高動態(tài)條件下,，載體動態(tài)會引起接收機中鎖相環(huán)（PLL）的不穩(wěn)定性,，無法直接采用載波相位測距提高位置估計精度,。而采用載波多普勒平滑偽距解算得到的位置存在較大的均值偏差。本文提出了一種基于差分信號的小波軌跡平滑算法,。仿真表明，該算法在載體最大加加速度為50 m/s3的條件下,，定位均值偏差小于0.04 m,，標(biāo)準(zhǔn)差小于1.3 m，在高動態(tài)條件下具有較高的定位精度,。
參考文獻(xiàn)
[1] DONOHO D L. De-noising by soft-thresholding [J].IEEE Transactions on Information Theory, 1995,41(3):613-627.
[2] 謝鋼. GPS原理與接收機設(shè)計[M]. 北京：電子工業(yè)出版社, 2009:128-129.
[3] BAH′RAMI M. Getting back on the sidewalk: Doppleraided autonomous positioning with single-frequency mass market receivers in urban areas[C].Proceedings of 22nd International Technical Meeting of the Satellite Division,Savannah, USA: Institute of Navigation, 2009:1716-1725.
[4] BARTONE C, ZHANG Y. A real-time hybrid-domain wave smooth code processing using wavelets[C]. Proceedings of 17th International Technical Meeting of the Satellite Division, Long Beach, USA: Institute of Navigation, 2004,436-446.
[5] 魯郁. GPS全球定位接收機——原理與軟件實現(xiàn)[M].北京: 電子工業(yè)出版社, 2009.
[6] 鄭亞弟.導(dǎo)航載體軌跡仿真系統(tǒng)的研究與開發(fā)[D].鄭州:解放軍信息工程大學(xué), 2006.
[7] DAUBECHIES I. Orthonormal bases of compactly supported wavelets [J]. Communications on pure and applied mathematics, 1988,41(7):909-996.

此內(nèi)容為AET網(wǎng)站原創(chuàng),，未經(jīng)授權(quán)禁止轉(zhuǎn)載。