摘   要： 介紹了AIN薄膜體聲波（FBAR）傳感器以及信號(hào)處理電路的原理，著重設(shè)計(jì)了傳感器的頻率檢測(cè)電路。頻率檢測(cè)電路采用VHDL語(yǔ)言對(duì)各個(gè)電路子模塊編寫(xiě)相應(yīng)的代碼,，并利用Quartus9.0完成了仿真,。仿真結(jié)果表明，相對(duì)精度為10-6,，達(dá)到了預(yù)期的設(shè)想,，滿(mǎn)足了FBAR傳感器的要求。
關(guān)鍵詞： FBAR,； 信號(hào)處理,； VHDL

    近年來(lái)，隨著射頻無(wú)線(xiàn)通信技術(shù)和半導(dǎo)體工藝的迅猛發(fā)展,，傳統(tǒng)的傳感器也正向微型化、智能化,、信息化轉(zhuǎn)變,。以薄膜體聲波諧振FBAR(Film Bulk Acoustic Wave)技術(shù)為基礎(chǔ)的微質(zhì)量傳感器因其具有體積小、頻率覆蓋范圍廣,、頻帶寬,、Q值高、帶外抑制高(大約50 dB),、功率容量大,、溫度系數(shù)小、可與半導(dǎo)體工藝兼容等優(yōu)勢(shì),，顯示出廣闊的應(yīng)用前景,。
    傳統(tǒng)的FBAR質(zhì)量傳感器由FBAR器件和信號(hào)處理電路組成。在實(shí)際應(yīng)用中,，為了使微質(zhì)量傳感器方便使用,，需要設(shè)計(jì)出一塊包含了信號(hào)處理和信號(hào)數(shù)字量讀取并輸出的電路[1]。由于FBAR微質(zhì)量傳感器的信號(hào)頻率為1 GHz~2 GHz甚至更高,，普通的CMOS電路直接對(duì)該頻率信號(hào)進(jìn)行采集處理難度比較大,，且難以保證精度。目前通常采用對(duì)頻率信號(hào)先用N分頻電路進(jìn)行分頻,，使FBAR的輸出頻率降至CMOS電路可以處理的頻率,，再進(jìn)行信號(hào)讀取。本文采用雙通道結(jié)構(gòu),，模擬與數(shù)字相結(jié)合的方法進(jìn)行信號(hào)的處理,先利用模擬電路進(jìn)行信號(hào)的處理,，再利用數(shù)字電路對(duì)處理過(guò)的信號(hào)進(jìn)行周期或者頻率的讀取。
1 系統(tǒng)構(gòu)成
    根據(jù)Rayleigh理論,機(jī)電系統(tǒng)的諧振本質(zhì)上是系統(tǒng)中動(dòng)能和勢(shì)能的平衡,，在FBAR表面加載一定微擾量的物質(zhì)后,，原先的能量平衡被破壞，為了實(shí)現(xiàn)新的平衡,，諧振頻率必然降低,，通過(guò)FBAR諧振頻率的變化可以反推出加載在表面微擾量的大小,。根據(jù)這個(gè)原理設(shè)計(jì)的信號(hào)處理電路結(jié)構(gòu)如圖1所示。該電路采用雙通道結(jié)構(gòu),，利用兩個(gè)FBAR振蕩器,，其中一路作為參考，另外一路作為傳感器吸附微小質(zhì)量,，由兩個(gè)振蕩頻率的差值可推算得到微小質(zhì)量的變化,。采用差分的方式可以消除FBAR工作環(huán)境因素的不利影響，同時(shí)可靠性和檢測(cè)精度也會(huì)得到提高[2],。

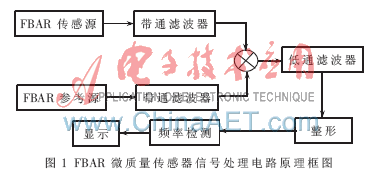
    FBAR微質(zhì)量傳感電路由振蕩,、混頻、濾波,、波形整形,、頻率檢測(cè)、顯示六部分組成,。在具體的設(shè)計(jì)中先利用正反饋原理,，采用電容式反饋?zhàn)孎BAR起振,將質(zhì)量變化的物理量轉(zhuǎn)化為正弦頻率的電信號(hào)，經(jīng)過(guò)Motorola的MC1596混頻器的混頻,，然后濾波,，最后通過(guò)搭建的整形電路進(jìn)行整形就可得到一個(gè)方波信號(hào)。頻率檢測(cè)是為了準(zhǔn)確地檢測(cè)這個(gè)方波信號(hào)的頻率,。
2 FPGA功能模塊
    在頻率檢測(cè)的模塊中,，以QuartusⅡ?yàn)殚_(kāi)發(fā)工具，分別對(duì)頻率檢測(cè)的各個(gè)模塊進(jìn)行了VHDL描述,。通過(guò)仿真驗(yàn)證其功能都得到了實(shí)現(xiàn),，最后的頂層設(shè)計(jì)仿真也說(shuō)明頻率檢測(cè)是符合要求的。頻率檢測(cè)先把經(jīng)過(guò)模擬電路處理好的信號(hào)送入量程選擇模塊,，選擇相應(yīng)的檔位,，一路信號(hào)送入小數(shù)點(diǎn)產(chǎn)生模塊，另外一路信號(hào)送入計(jì)數(shù)時(shí)鐘和閘門(mén)產(chǎn)生模塊,；經(jīng)過(guò)對(duì)石英晶振和被測(cè)信號(hào)的二分頻產(chǎn)生計(jì)數(shù)時(shí)鐘和閘門(mén)信號(hào),，再送入周期測(cè)量模塊測(cè)出被測(cè)信號(hào)的周期，按照需要還可以把信號(hào)送入除法器得到頻率,；最后通過(guò)選擇器來(lái)選擇周期或者頻率并送入相對(duì)應(yīng)小數(shù)點(diǎn)的模塊,，最終送入顯示模塊。其電路框圖如圖2所示,。

2.1量程選擇模塊
    量程選擇模塊主要實(shí)現(xiàn)一個(gè)周期測(cè)量的計(jì)數(shù)器,，用被測(cè)信號(hào)周期作為閘門(mén)的長(zhǎng)度，用晶振時(shí)鐘作為計(jì)數(shù)時(shí)鐘，根據(jù)所記的數(shù)值來(lái)選擇量程編號(hào),。該模塊采用7位 BCD計(jì)數(shù)器計(jì)數(shù),。把被測(cè)信號(hào)進(jìn)行二分頻然后送入到計(jì)數(shù)器的清零端，即可實(shí)現(xiàn)被測(cè)信號(hào)的二分頻為低電平進(jìn)行計(jì)數(shù)器計(jì)數(shù),在被測(cè)信號(hào)的二分頻為高電平時(shí)清零,。7位BCD計(jì)數(shù)器主要輸出2路信號(hào),，一個(gè)為進(jìn)位信號(hào)count，另外一個(gè)為標(biāo)志每一位BCD數(shù)zeros[6,0]是否為0,根據(jù)zeros[6,0]通過(guò)簡(jiǎn)單的組合邏輯譯碼電路即可選擇量程編號(hào),。輸出結(jié)果通過(guò)寄存器鎖存,，當(dāng)計(jì)數(shù)器清零時(shí)，結(jié)果仍然保存在寄存器中,。寄存器中的數(shù)據(jù)通過(guò)一個(gè)組合邏輯的譯碼電路顯示出最終所需要的量程編號(hào),。
    從圖3所示仿真波形可見(jiàn)， 當(dāng)被測(cè)信號(hào)的頻率為25 kHz時(shí)得到量程5,，符合前面的分析,。

2.2時(shí)鐘和閘門(mén)模塊
     時(shí)鐘信號(hào)可能是晶振時(shí)鐘或者晶振時(shí)鐘的10分頻，閘門(mén)信號(hào)可能是待測(cè)信號(hào)的10分頻,、102分頻、103分頻,、104分頻,、105分頻、106分頻,。而閘門(mén)信號(hào)的分頻問(wèn)題可用量程估計(jì)模塊所用的zeros[6,0]解決,。例如zeros(2)代表7位 BCD計(jì)數(shù)器的百位是否為0。假如要實(shí)現(xiàn)103分頻,，則zeros(2)為高電平占100個(gè)計(jì)數(shù)周期,，zeros(2)為低電平占900個(gè)周期。時(shí)鐘信號(hào)是晶振時(shí)鐘或者晶振時(shí)鐘的10分頻,，晶振時(shí)鐘的10分頻可通過(guò)1個(gè)模為10的計(jì)數(shù)器輕松實(shí)現(xiàn),。
    時(shí)鐘和閘門(mén)模塊仿真波形如圖4所示。圖中被測(cè)信號(hào)的頻率為25 kHz,輸出的時(shí)鐘為10 MHz,，輸出的閘門(mén)信號(hào)gate寬度為40 ms,。

2.3 周期計(jì)數(shù)模塊
    周期計(jì)數(shù)模塊使用一個(gè)7位BCD計(jì)數(shù)來(lái)實(shí)現(xiàn)計(jì)數(shù)的穩(wěn)定輸出，采用2個(gè)寄存器來(lái)實(shí)現(xiàn),。通過(guò)前1個(gè)寄存器實(shí)現(xiàn)清零不鎖存數(shù)據(jù),，后1個(gè)寄存器實(shí)現(xiàn)清零鎖存數(shù)據(jù)[3]。最終實(shí)現(xiàn)了不輸出中間計(jì)數(shù)結(jié)果,、只穩(wěn)定輸出最終結(jié)果的目的,。周期計(jì)數(shù)模塊仿真波形如圖5所示。

    當(dāng)閘門(mén)信號(hào)分別為100 ?滋s和10 μs時(shí)，因?yàn)楸粶y(cè)信號(hào)經(jīng)過(guò)二分頻才產(chǎn)生閘門(mén)信號(hào),，所以被測(cè)信號(hào)為50 μs和5 μs,，圖5中的相應(yīng)的輸出值為49.9μs和4.9 λs，兩者的誤差都不大,。
2.4 除法器模塊
    除法器模塊的任務(wù)是周期到頻率的轉(zhuǎn)換,。為了保證精度，決定輸出結(jié)果也采用7位BCD數(shù),。這樣被除數(shù)就需要達(dá)到1013,。因?yàn)榍懊鏋榱耸褂?jì)數(shù)都達(dá)到106~107，閘門(mén)的寬度經(jīng)過(guò)不同程度的分頻,，時(shí)間都在0.1 s~1 s,，除法器可以采用時(shí)序較慢的時(shí)序邏輯電路。這就意味著可以把除法運(yùn)算轉(zhuǎn)化成減法運(yùn)算,，相當(dāng)于1013減去多少個(gè)閘門(mén)時(shí)間T[4],。因?yàn)楦?位只是借位，實(shí)際發(fā)生變化的是低7位,。因此,，為了實(shí)現(xiàn)除法運(yùn)算，需要一個(gè)7位減法器來(lái)運(yùn)算低7位被除數(shù)減去除數(shù)T,，需要一個(gè)減法計(jì)數(shù)器來(lái)保存被除數(shù)高7位BCD數(shù),，還需要一個(gè)7位 BCD加法器來(lái)保存做過(guò)的減法運(yùn)算的次數(shù)。除法器的結(jié)構(gòu)框圖如圖6所示,。

    這里還涉及了一個(gè)狀態(tài)轉(zhuǎn)換,，于是采用了狀態(tài)機(jī)這個(gè)概念。狀態(tài)機(jī)相當(dāng)于一個(gè)電路控制系統(tǒng),，負(fù)責(zé)寄存器的被除數(shù)和除數(shù)的加載,、清零以及計(jì)數(shù)器的清零和計(jì)數(shù)等功能[5]。狀態(tài)s0表示就緒狀態(tài),，負(fù)責(zé)各個(gè)寄存器和計(jì)數(shù)器的清零和加載,。s0持續(xù)一個(gè)晶振周期后自動(dòng)轉(zhuǎn)換到s1。在s1狀態(tài)下,，做減法運(yùn)算,，直到7位 BCD減法計(jì)數(shù)器為0，代表被除數(shù)高7位全部借完,，此時(shí)狀態(tài)s1結(jié)束,，轉(zhuǎn)為狀態(tài)s2，即把7 位 BCD加法器的結(jié)果輸出到寄存器B,。
    圖7所示為除法器的仿真波形,?？梢钥吹剑瑺顟B(tài)機(jī)先從001(s0)經(jīng)過(guò)1個(gè)周期的等待無(wú)條件地轉(zhuǎn)換到010(s1),；當(dāng)zeros產(chǎn)生高電平,，即借位完畢時(shí)再轉(zhuǎn)換到100(s2)并輸出結(jié)果。

2.5 小數(shù)點(diǎn)模塊
    由于精度的要求,，改變了閘門(mén)的大小,，使讀數(shù)始終保持106~107，這就需要小數(shù)模塊來(lái)實(shí)現(xiàn)讀數(shù)的準(zhǔn)確化,。因?yàn)榧偃缱x數(shù)都是4×106,，如果沒(méi)有小數(shù)點(diǎn)的選擇，將不知道這個(gè)數(shù)到底表示多大的周期或者頻率,。小數(shù)點(diǎn)的顯示與量程的選擇其實(shí)是一一對(duì)應(yīng)的,。例如0.01 μs，小數(shù)點(diǎn)控制位顯示0000100,。在周期模式里,，小數(shù)對(duì)應(yīng)方式為：量程0對(duì)應(yīng)0000001，量程1對(duì)應(yīng)0000010,，量程2對(duì)應(yīng)0000100,，量程3對(duì)應(yīng)0001000，量程4對(duì)應(yīng)0010000,，量程5對(duì)應(yīng)0100000,，量程6對(duì)應(yīng)1000000，量程7對(duì)應(yīng)1111111,。在頻率模式下，小數(shù)對(duì)應(yīng)方式為：量程0對(duì)應(yīng)1111111,，量程1對(duì)應(yīng)1000000,，量程2對(duì)應(yīng)0100000，量程3對(duì)應(yīng)0010000,，量程4對(duì)應(yīng)0001000,，量程5對(duì)應(yīng)0000100，量程6對(duì)應(yīng)0000010,，量程7對(duì)應(yīng)0000001,。小數(shù)點(diǎn)仿真波形如圖8所示。

    由圖可知,，5 MHz的被測(cè)信號(hào)的周期為0.2 s,實(shí)驗(yàn)所得為0.199 999 9s,，相對(duì)誤差為1×10-6。
    本設(shè)計(jì)通過(guò)模擬電路和數(shù)字電路的結(jié)合,，實(shí)現(xiàn)了微質(zhì)量傳感器把質(zhì)量向頻率的轉(zhuǎn)換,，并能準(zhǔn)確地顯示出該信號(hào)的頻率或者周期,。通過(guò)對(duì)所設(shè)計(jì)的電路的仿真和實(shí)驗(yàn)，驗(yàn)證了其可行性,。
參考文獻(xiàn)
[1] 王振紅.VHDL與數(shù)字電路設(shè)計(jì)與應(yīng)用實(shí)踐教程[M]. 北京：機(jī)械工業(yè)出版社,，2006.
[2] 王永良,宋政湘.基于FPGA的同步測(cè)周期高精度數(shù)字頻率計(jì)的設(shè)計(jì)[J]. 電子設(shè)計(jì)應(yīng)用，2004(12):74-76.
[3] 駱舒萍.基于QuartusⅡ軟件平臺(tái)的八位數(shù)字頻率計(jì)設(shè)計(jì)[J]. 漯河職業(yè)技術(shù)學(xué)院學(xué)報(bào),，2011,10(2):20-23.
[4] 楊守良.基于FPGA的數(shù)字頻率計(jì)的設(shè)計(jì)和實(shí)現(xiàn)[J].現(xiàn)代電子技術(shù),，2005(11):118-120.
[5] 劉昌華.數(shù)字邏輯EDA設(shè)計(jì)與實(shí)踐[M]. 北京：國(guó)防工業(yè)出版社，2006.