摘 要： 研究了一種基于差分法原理的MS跟蹤算法。當(dāng)MS跟蹤目標(biāo)位置發(fā)生較大偏移時(shí),，通過使用差分法提取的目標(biāo)形心位置對其進(jìn)行修正,。實(shí)驗(yàn)結(jié)果表明，該方法應(yīng)用于運(yùn)動目標(biāo)的跟蹤具有良好的跟蹤效果,。
關(guān)鍵詞： 幀差法,；目標(biāo)提取；目標(biāo)跟蹤,；均值漂移
近年來,，目標(biāo)跟蹤是機(jī)器視覺領(lǐng)域比較活躍的研究課題，在車輛跟蹤,、智能機(jī)器人,、人機(jī)交互、智能家居以及生物醫(yī)學(xué)圖像分析等行業(yè)有著潛在的應(yīng)用[1-2],。學(xué)者們提出了大量的運(yùn)動目標(biāo)跟蹤算法,，在這些算法中，基于統(tǒng)計(jì)迭代思想的均值漂移MS（Mean Shift）算法,，經(jīng)常被應(yīng)用于聚類,、圖像平滑、圖像分割和跟蹤等各種不同場合,。該方法計(jì)算量不大,，能夠進(jìn)行視頻圖像的目標(biāo)跟蹤[3]。
目前,，MS方法在計(jì)算機(jī)視覺領(lǐng)域的應(yīng)用飛速發(fā)展,。COMAIVICIU D成功地將MS方法應(yīng)用到圖像分割和目標(biāo)跟蹤中[4]。應(yīng)用Lindeberg理論解決了MS方法在跟蹤色塊時(shí)特征空間尺度h的選取問題[5],。彭寧嵩等證明了在核函數(shù)窗寬固定的條件下,，目標(biāo)在其窗寬范圍內(nèi)進(jìn)行縮放,、平移運(yùn)動并不影響Mean Shift跟蹤算法空間定位的準(zhǔn)確性[6]。賈靜平等引入目標(biāo)傾角的方法來跟蹤旋轉(zhuǎn)的目標(biāo)[7],，但是該方法是采用試探的方法通過多次分別計(jì)算水平,、垂直和旋轉(zhuǎn)的自由度，然后分別取最優(yōu)值,。這種方法比較復(fù)雜,，而且采用固定的變化大小，對目標(biāo)變化的適應(yīng)性不強(qiáng),。以上這些方法雖然在某些場合下跟蹤效果比較滿意,，然而算法比較復(fù)雜、計(jì)算量大,。
基于MS的目標(biāo)跟蹤算法要求相鄰兩幀間目標(biāo)位置必須有重合,，因此，當(dāng)目標(biāo)的運(yùn)動速度較小時(shí),，能夠獲得比較理想的跟蹤結(jié)果,。當(dāng)目標(biāo)運(yùn)動速度較快且目標(biāo)較小導(dǎo)致相鄰兩幀間的目標(biāo)位置無重合時(shí)，該方法往往失效,。差分法是常用的目標(biāo)提取算法，可以快速有效地提取出目標(biāo)的輪廓,。利用差分法提取出目標(biāo)的輪廓,，進(jìn)而計(jì)算出目標(biāo)的形心位置，從而為MS跟蹤算法提供準(zhǔn)確,、可靠的目標(biāo)位置,。本文主要研究動態(tài)復(fù)雜背景下圖像序列中運(yùn)動目標(biāo)的跟蹤技術(shù)。利用MS理論和差分法目標(biāo)提取算法相結(jié)合,，實(shí)現(xiàn)了運(yùn)動目標(biāo)的跟蹤,。通過對行駛中的小汽車的跟蹤，驗(yàn)證了本文算法的有效性,。
1 差分法目標(biāo)分割及特征提取
差分法也叫幀差法,，是用當(dāng)前幀圖像減去前一幀圖像，提取出運(yùn)動目標(biāo),，屬于圖像分割技術(shù)范疇,，其原理比較簡單，易于實(shí)現(xiàn),。
1.1 差分法原理
基于像素灰度信息的差分算法速度快,、提取準(zhǔn)確，是運(yùn)動目標(biāo)提取首選算法,。假定函數(shù)fk（x,，y）,、fk+1（x，y）分別表示第k幀,、第k+1幀圖像（x,，y）處的像素值，則差分操作定義為：
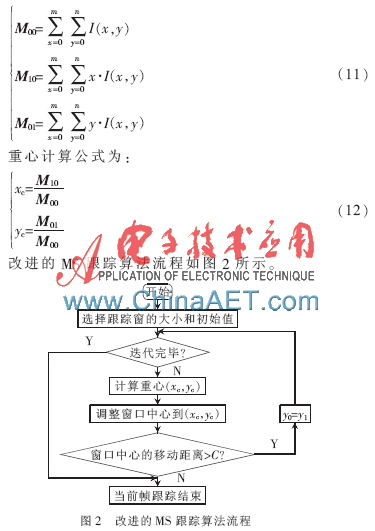
一般來說,，MS算法迭代若干次（一般在10次以內(nèi)）后就可以逼近準(zhǔn)確值,。關(guān)于MS算法的收斂性，可參閱參考文獻(xiàn)[10],。改進(jìn)算法中的C為一個(gè)極小正數(shù),，通常取0.5，即半個(gè)像素,。
3 實(shí)驗(yàn)結(jié)果與分析
3.1 跟蹤算法仿真實(shí)驗(yàn)
為了驗(yàn)證本文所提出的目標(biāo)跟蹤算法的性能,，采用兩組視頻圖像進(jìn)行測試，并比較MS跟蹤算法與本文跟蹤算法的跟蹤效果,。所有算法均在Intel Pentium 4 3.0 GHz CPU,、2 GB內(nèi)存計(jì)算機(jī)，Windows XP系統(tǒng)下用MATLAB 7.9編程實(shí)現(xiàn),。圖像中方框表示估計(jì)的目標(biāo)位置,，在圖像序列中待跟蹤目標(biāo)的初始位置手動給定。
圖3是對一段長為70幀,，幀速率為15 f/s的視頻圖像中沿著斜坡滾動下落小球的跟蹤實(shí)驗(yàn)結(jié)果,。其中,圖3（a）是利用MS算法對第8、15,、27,、36、50和60幀圖像中運(yùn)動小球的跟蹤結(jié)果,，圖3（b）是利用改進(jìn)算法對相對應(yīng)的幀圖像中運(yùn)動小球的跟蹤結(jié)果,。
3.2 跟蹤算法評價(jià)
跟蹤方法的性能主要從精確度和實(shí)時(shí)性上進(jìn)行評定。精確度主要是測試應(yīng)用該算法在各種環(huán)境中能否比較準(zhǔn)確地跟蹤初始化的目標(biāo),。為此需要計(jì)算跟蹤偏差,。
定義第i幀圖像中目標(biāo)位置的偏差ei為：
ei=|Ti-Ci| （13）
其中,，Ti表示在第i幀圖像中跟蹤目標(biāo)中心的位置,；Ci表示在第i幀圖像中目標(biāo)中心的準(zhǔn)確位置，Ci的值可以通過人工的方式獲得,。
定義目標(biāo)跟蹤的平均偏差為：
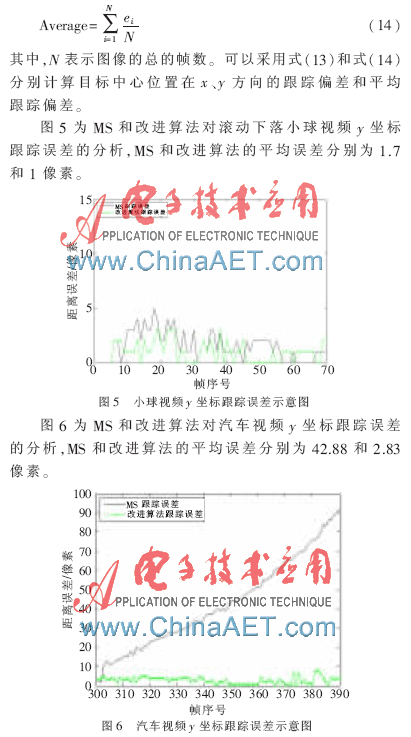
本文提出了一種基于差分法的改進(jìn)Mean Shift目標(biāo)跟蹤算法,。通過差分法進(jìn)行目標(biāo)提取并計(jì)算目標(biāo)的重心坐標(biāo)，對Mean Shift算法進(jìn)行自動修正,。在目標(biāo)丟失時(shí),，通過差分法修正跟蹤位置,，重新進(jìn)行目標(biāo)定位來獲得穩(wěn)定的跟蹤。這種方法在跟蹤偏移的情況下能夠調(diào)整算法的目標(biāo)模型分布,，從而修正Mean Shift的跟蹤過程,。實(shí)驗(yàn)結(jié)果表明，本文所提出的方案實(shí)現(xiàn)了對運(yùn)動目標(biāo)的提取與跟蹤,。本文算法不足之處是沒有考慮目標(biāo)在運(yùn)動時(shí)大小的變化,，因此下一步的工作是研究跟蹤窗口隨著目標(biāo)大小變化的自適應(yīng)窗口跟蹤。
參考文獻(xiàn)
[1] 蔡榮太.非線性自適應(yīng)濾波器在電視跟蹤中的應(yīng)用[D].北京：中國科學(xué)院,，2008.
[2] 王亮,，胡衛(wèi)明，譚鐵牛.人運(yùn)動的視覺分析綜述[J].計(jì)算機(jī)學(xué)報(bào),，2002,，25（3）：225-237.
[3] COMANIEIU D， RAMESH V. Mean Shift and optimal Prediction for efficient object tracking[C]. Proceedings of the IEEE Conference on Image,， 2000（3）：70-73.
[4] COMANICIU D,， MEER P. Robust analysis of feature spaces： color image segmentation[M]. Los Alamitos， USA,， 1997： 750-755.
[5] COLLINS,， ROBERT T. Mean-shift blob tracking through scale space[D]. United States： Institute of Electrical and Electronics Engineers Computer Society， 2003.
[6] 彭寧嵩,，楊杰,，劉志，等.Mean Shift跟蹤算法中核函數(shù)窗寬的自動選取[J].軟件學(xué)報(bào),，2005：1542-1550.
[7] 賈靜平，張艷寧,，柴艷妹,，等.目標(biāo)多自由度Mean Shift序列圖像跟蹤算法[J].西北工業(yè)大學(xué)學(xué)報(bào)，2005,，23（5）：618-622.
[8] FUKUNAGA K,， HOSTETLER L D. The estimation of the gradient of a density function with applications in pattern recognition[J]. IEEE Transactions on Information Theory， 1975,，21（1）：32-40.
[9] COMANICIU D,， MEER P. Mean Shift： a robust approach toward feature space analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2002,，24（5）：564-577.
[10] 李鄉(xiāng)儒,，吳福朝，胡占義.均值漂移算法的收斂性[J].軟件學(xué)報(bào),，2005,，16（3）：365-374.