0 引言

　　圖挖掘問題[1-3]在移動(dòng)互聯(lián)網(wǎng)、大數(shù)據(jù)處理等領(lǐng)域具有十分重要的應(yīng)用價(jià)值,，是目前的研究熱點(diǎn),。文獻(xiàn)[4]提出了一種基于共生頻繁項(xiàng)樹和逆矩陣的圖挖掘算法。文獻(xiàn)[5]中的SpiderMine算法采用概率挖掘理論來尋找前K個(gè)最大模式,，通過將小規(guī)模高頻率模式融合為大規(guī)模模式,，克服了算法瓶頸，效率較高,。文獻(xiàn)[6]提出了一種自適應(yīng)云端的大規(guī)模導(dǎo)出子圖提取算法,，以解決資源優(yōu)化利用與海量圖挖掘等問題,。文獻(xiàn)[7]提出一種圖形挖掘系統(tǒng)OPAvion。然而,，上述方法均無法進(jìn)行云環(huán)境下大規(guī)模圖形的高頻率模式挖掘,。為了解決以上問題，本文針對文獻(xiàn)[5]中的SpiderMine算法提出云環(huán)境下的新算法c-SpiderMine,。c-SpiderMine包括分區(qū),、挖掘、融合3個(gè)階段,。分區(qū)階段利用最小切割算法將大規(guī)模圖形數(shù)據(jù)分為多個(gè)子圖,，使分區(qū)/融合成本最小。第2階段為挖掘階段,，利用SpiderMine進(jìn)行模式挖掘,，利用約簡器可有效降低圖形同構(gòu)測試的成本，顯著降低大型模式生成時(shí)的組合復(fù)雜度,。更重要的是,，本文構(gòu)建一個(gè)全局表格以避免該階段出現(xiàn)不對稱信息，最后一個(gè)階段是模式融合,。本文提出一種模式鍵(Pattern Key,，PK)函數(shù)來保存模式，以保證所有模式可被成功恢復(fù)和融合,。

1 問題描述

　　1.1 圖分割

　　將輸入的數(shù)據(jù)圖表示為G,，將分割數(shù)據(jù)集表示為S。圖分割問題可定義如下：

　　定義1：已知圖形G=(V,，E),，切邊集合C(Ec)，其中Ec將G分為多個(gè)分區(qū){S1,，S2,，…，Sn},，且對任意i≠j有Ui Si=V,。切邊集合Ec為頂點(diǎn)屬于不同分區(qū)的邊集合。

　　1.2 不對稱信息

　　基于經(jīng)典的MapReduce[8]模型,，本文在分區(qū)階段將圖形G分割為多個(gè)子圖S1,，S2，…,，Sn,。在挖掘階段，需要挖掘初始時(shí)頻率較低的圖形模式，稱為spider,，定義2中對此進(jìn)行描述,。

　　定義2：將半徑約束在r范圍內(nèi)的高頻率模式稱為r-spider。用圖形的頭部表示每個(gè)spider,，Spider的半徑為其節(jié)點(diǎn)的最小偏心率,，因此，radius(spider)=min{e(v):v∈V(spider)},。

　　1.3 模式融合

　　在融合階段,，將利用挖掘階段生成的spider生成全局高頻率模式。這一問題的簡單求解方法是發(fā)送spider然后對其融合,。然而,，如果在一臺(tái)機(jī)器上融合所有圖形，則將產(chǎn)生兩個(gè)問題,。首先,，約簡程序的存儲(chǔ)空間無法從所有映射程序中讀取所有的高頻率子圖，因?yàn)楦哳l率模式集合的數(shù)據(jù)規(guī)模大于原始的輸入圖形規(guī)模,。其次,，難以定義合適的融合鍵值。對鍵值做普通選擇會(huì)復(fù)制切割節(jié)點(diǎn),。然而,，選擇這些節(jié)點(diǎn)作為鍵值會(huì)導(dǎo)致部分大規(guī)模模式無法被融合。

2 c-SpiderMine算法

　　圖1給出了本文方法的框架,。

　　2.1 分割階段

　　本文采用最小切邊算法來進(jìn)行圖分割,。最小切邊集合概念見定義3。

　　定義3：已知圖形G(V,，E),，其中V表示頂點(diǎn)結(jié)合，E表示邊緣集合,，G(V,，E)的最小切邊集合Ec(S，T)可將V分割為S且T=V-S,，同時(shí)有s∈S,，t∈T，且Ec(S,，T)=Ec(u,，v)的容量最小,。

　　為了將圖形G(V,，E)分割為k個(gè)均勻子圖且每個(gè)子圖均能保留其結(jié)構(gòu)，首先利用最小切邊集合Ec將一個(gè)圖形分割為多個(gè)子圖，然后,，在u和v分別隸屬的兩個(gè)子圖中,，復(fù)制最小切邊集合Ec上的所有節(jié)點(diǎn)對(u，v),。該階段算法見算法1,。

　　算法1：分割階段

　　要求：圖G=(V，E)

　　k：圖形分割數(shù)量

　　輸出：Gsub={g1,，…,，gk}，G被分割的子圖

　　1： Gsub←k-Partition(G,，k)

　　2： for 每個(gè)gi,，gj∈Gsub  do

　　3： Ec←{(vi，vj)|vi∈gi(V),，vj∈gj(V)}

　　//添加gi和gj中的切邊集合Ec

　　4： gi(E)←gi(E)∪Ec

　　//添加gi的切割節(jié)點(diǎn)集合Vc的連通邊緣

　　5： gi(E)←gi(E)∪{(vi,，vj)|vi∈Ec|vj∈Ec∧i≠j}

　　6： 輸出所有子圖Gsub

　　2.2 挖掘階段

　　在挖掘階段的第1步，采用文獻(xiàn)[9]中提出的模式增長算法實(shí)現(xiàn)spider增長,，以便在半徑約束內(nèi)挖掘所有的高頻率圖形模式,，它只需一個(gè)處理器就可獲得所有的初始spider。在該階段中,，首先需要選擇一個(gè)節(jié)點(diǎn)作為初始模式,。然后，算法利用與模式相連的邊來擴(kuò)展模式,，進(jìn)而生成新的候選,。算法還收集模式嵌入因子。如果嵌入因子數(shù)量低于支持閾值,，則算法修剪候選,。為了實(shí)現(xiàn)spider的并行增長，本文采用BSP模型來增長相同深度內(nèi)不同子圖中的spider,，即可以在同一超級步驟內(nèi)生成邊緣和節(jié)點(diǎn)數(shù)量相同的所有高頻率spider候選,。在挖掘階段的第2步中，通過構(gòu)建一個(gè)全局表來維護(hù)每個(gè)spider候選的支持?jǐn)?shù),。在同頻率圖形模式候選集合增長期間,，通過Canonical forms[10]對候選模式進(jìn)行編碼，將每個(gè)候選模式的本地支持量發(fā)送給全局表,。然后,，在超級步驟結(jié)束后修剪頻率較低的候選，并確保所有處理器均增加了候選的可能嵌入因子數(shù),。通過這種方法可以保證不會(huì)有模式由于信息不對稱而被修剪,。挖掘階段的整個(gè)步驟見算法2,。

　　算法2：MiningPhase（挖掘階段）

　　要求：Gsub：分割后的子圖

　　r：圖形半徑

　　最小支持閾值

　　輸出：〈Ec(Gid)，S′〉,，Gsub中的切邊集合和高頻率圖形模式集合

　　Map(Key k,，Value v)

　　1： Gid←k//鍵定義為子圖ID

　　2： Gsub←v//值定義為子圖數(shù)據(jù)

　　3： 利用標(biāo)識(shí)頻率對Gsub中所有節(jié)點(diǎn)進(jìn)行同步和排序

　　4： for all gi∈Gsub do

　　5： 修剪低頻率標(biāo)識(shí)，重新標(biāo)識(shí)gi的節(jié)點(diǎn)

　　6： 輸出〈Gid,，Gsub〉

　　Reduce(Key k,，Values v[])

　　1： Gid←k//鍵為子圖ID

　　2： Gsub←v//值為子圖數(shù)據(jù)

　　3： S1←Gsub中所有本地高頻率單邊圖形

　　4： for 每個(gè)s∈S1 do

　　5： supglobal(s)←CalculateSupport(s)

　　6： S∈S1；

　　7： if  S≠?覫 do

　　8：  for 每個(gè)s∈S  do

　　9：    if supglobal(s)<?茲且Radius(s)≠r then

　　10：S′←S-{s}

　　11：    else

　　12：S′←GrowPattern{s}

　　//生成候選圖形模式并更新supglobal

　　13：sync(s,，supglobal)//BSP模型同步

　　14： 輸出〈Ec(Gid),，S′〉

　　2.3 融合階段

　　融合階段包括兩個(gè)MapReduce任務(wù)。第1個(gè)任務(wù)是將不同子圖中的spider擴(kuò)展為更大規(guī)模的模式,。為了解決融合問題,，文中提出一種基于重疊的模式鍵(Pattern Key，PK)函數(shù),。鍵(key)定義為每個(gè)高頻率圖形模式候選的哈希碼,，值(value)定義為候選spider每個(gè)子圖中嵌入因子數(shù)的支持?jǐn)?shù)之和。PK函數(shù)的作用在于保留初始關(guān)系,，提供兩個(gè)子圖間的關(guān)聯(lián),。PK函數(shù)的定義見定義4。

　　定義4：已知一個(gè)子圖g(V,，E),，其中V表示節(jié)點(diǎn)集合，E表示邊集,，Vc表示復(fù)制節(jié)點(diǎn)集,。將切割節(jié)點(diǎn)vc∈Vc的重疊切割節(jié)點(diǎn)集定義。

　　第2個(gè)任務(wù)稱為模式修剪任務(wù),，內(nèi)容是當(dāng)兩個(gè)模式同形時(shí)修剪掉重復(fù)的模式,。模式修剪任務(wù)之后，可以計(jì)算每個(gè)模式的支持?jǐn)?shù),。最后,，將所有模式發(fā)送給模式融合任務(wù)。因?yàn)楸疚囊呀?jīng)在先前的任務(wù)中修剪掉了低頻率模式并進(jìn)行了同構(gòu)測試,，所以通過檢查兩個(gè)模式是否擁有相同的PK來進(jìn)行模式融合,。如果兩個(gè)模式的PK相同，則通過該相同的spider對其融合,。重復(fù)這一步驟,，直到新生成的模式的直徑超出直徑界限為止。限于篇幅,，融合階段的詳細(xì)步驟在此略去,。

3 仿真實(shí)驗(yàn)

　　3.1 實(shí)驗(yàn)環(huán)境

　　本文在33個(gè)虛擬機(jī)構(gòu)成的云計(jì)算環(huán)境下,，將c-SpiderMine部署于HAMA 0.5和Hadoop 1.0.3上，其中一個(gè)節(jié)點(diǎn)作為主節(jié)點(diǎn),，其余節(jié)點(diǎn)均作為從屬節(jié)點(diǎn),。所有實(shí)驗(yàn)運(yùn)行于256 GB內(nèi)存和1 GB以太網(wǎng)英特爾Xeon服務(wù)器平臺(tái)上,。

　　3.2 與SpiderMine的比較

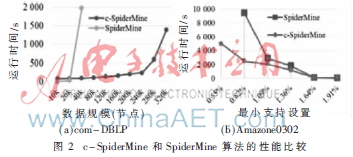
　　為了證明c-SpiderMine的有效性,，選擇SpiderMine作為基準(zhǔn)算法來比較節(jié)點(diǎn)數(shù)量不同時(shí)的運(yùn)行時(shí)間，最小支持?jǐn)?shù)不同時(shí)的運(yùn)行時(shí)間及內(nèi)存使用情況,。從網(wǎng)站上選擇兩種大型數(shù)據(jù)集[11]進(jìn)行測試,，如圖2(a)所示，當(dāng)節(jié)點(diǎn)規(guī)模變大時(shí)運(yùn)行時(shí)間上升,，在該圖中,，可以發(fā)現(xiàn)當(dāng)數(shù)據(jù)規(guī)模大于20 000時(shí)，SpiderMine難以為圖形提供支持,，相反,，當(dāng)數(shù)據(jù)規(guī)模增大時(shí)，c-SpiderMine的性能較優(yōu),。圖2(b)表明即使最小支持?jǐn)?shù)較低,，c-SpiderMine在運(yùn)行時(shí)間方面的性能仍優(yōu)于SpiderMine。此外,，可以發(fā)現(xiàn)當(dāng)最少支持?jǐn)?shù)低于0.82%時(shí),，c-SpiderMine優(yōu)于SpiderMine?？傮w來說,，本文c-SpiderMine方法在處理大規(guī)模圖形數(shù)據(jù)時(shí)顯示出了良好的運(yùn)行時(shí)間性能，降低了內(nèi)存使用量,，且效率高于SpiderMine,。

　　3.3 伸縮性

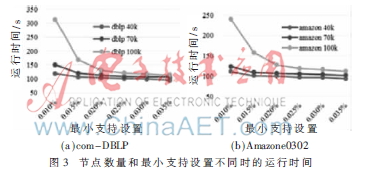
　　(1)最小支持設(shè)置的影響：下面分別在圖3(a)和3(b)中給出com-DBLP和Amazone0302的運(yùn)行時(shí)間。兩組實(shí)驗(yàn)的最小支持設(shè)置范圍為0.01%-0.035%,，節(jié)點(diǎn)規(guī)模分別為40 000,、70 000和100 000。結(jié)果表明,，當(dāng)最小支持設(shè)置增加時(shí),，運(yùn)行時(shí)間下降。這表明,，當(dāng)最小支持設(shè)置增加時(shí),，生成的模式數(shù)量變小，運(yùn)行時(shí)間降低,。此外,，當(dāng)N增加時(shí),，運(yùn)行時(shí)間同步增加，明顯表明有更多的節(jié)點(diǎn)生成更多的模式,，消耗更多的時(shí)間,。實(shí)驗(yàn)表明，當(dāng)節(jié)點(diǎn)規(guī)模和最小支持?jǐn)?shù)增加時(shí),，c-SpiderMine在運(yùn)行時(shí)間方面具有良好的伸縮性,。

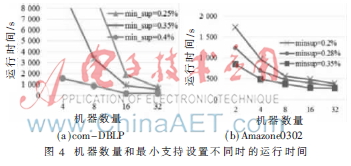
　　(2)機(jī)器數(shù)量的影響：本節(jié)研究了機(jī)器數(shù)量不同時(shí)的性能。驗(yàn)證c-SpiderMine的性能時(shí),，對com-DBLP數(shù)據(jù)集使用4,、8、16和32臺(tái)機(jī)器,，最小支持設(shè)置為0.25%,、0.35%和0.4%，對Amazone0302數(shù)據(jù)集使用2,、4,、8、16和32臺(tái)機(jī)器,，最小支持設(shè)置為0.2%,、0.28%和0.35%。在圖4(a)和4(b)中,，當(dāng)機(jī)器數(shù)量上升時(shí)運(yùn)行時(shí)間呈指數(shù)下降,。結(jié)果表明，機(jī)器數(shù)量增加可提高性能和效率,，這進(jìn)一步證明云計(jì)算可直接提高大規(guī)模圖形數(shù)據(jù)挖掘的伸縮性,。

4 結(jié)論

　　本文提出了c-SpiderMine算法，在處理大規(guī)模圖形數(shù)據(jù)時(shí)有效融合了BSP模型,、SpiderMine和云計(jì)算,。實(shí)驗(yàn)結(jié)果表明，在不同數(shù)據(jù)規(guī)模和最小支持設(shè)置條件下,，c-SpiderMine在內(nèi)存使用和運(yùn)行時(shí)間方面的性能均優(yōu)于SpiderMine,。文中還證明了c-SpiderMine在不同的最小支持設(shè)置和機(jī)器數(shù)量條件下，具有良好的伸縮性,。在下一步工作中,，可結(jié)合更多的真實(shí)大型數(shù)據(jù)集對本文方法展開研究。

參考文獻(xiàn)

　　[1] 孫鶴立,，陳強(qiáng),，劉瑋，等.利用MapReduce平臺(tái)實(shí)現(xiàn)高效并行的頻繁子圖挖掘[J].計(jì)算機(jī)科學(xué)與探索,，2014,，8(7)：790-801.

　　[2] ANCHURI P,，ZAKI M J，BARKOL O,，et al.Approximate graph mining with label costs[C].Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining.ACM,，2013：518-526.

　　[3] KANG U，AKOGLU L,，CHAU D H P.Big graph mining：algorithms,，anomaly detection，and applications[J].Proceedingsof the ACM ASONAM,，2013,，13：25-28.

　　[4] 李濤,，肖南峰.基于共生頻繁項(xiàng)樹和逆矩陣的圖挖掘[J].計(jì)算機(jī)應(yīng)用研究,，2014，31(10)：2916-2919.

　　[5] ZHU F,，QU Q,，LO D，et al.Mining top-k large structural patterns in a massive network[J].Proceedings of the VLDB Endowment,，2011,，4(11)：807-818.

　　[6] 郭鑫，董堅(jiān)峰,，周清平.自適應(yīng)云端的大規(guī)模導(dǎo)出子圖提取算法[J].計(jì)算機(jī)科學(xué),，2014，41(6)：155-160.

　　[7] AKOGLU L,，CHAU D H,，KANG U，et al.Opavion：mining and visualization in large graphs[C].Proceedings of the 2012ACM SIGMOD International Conference on Management of Data.ACM,，2012：717-720.

　　[8] SARMA A D,，AFRATI F N，SALIHOGLU S,，et al.Upper and lower bounds on the cost of a map-reduce computa-tion[C].Proceedings of the VLDB Endowment. VLDB Endowment,，2013，6(4)：277-288.

　　[9] BORGELT C,，MEINL T,，BERTHOLD M.Moss：a program for molecular substructure mining[C].Proceedings of the 1st international workshop on open source data mining：frequentpattern mining implementations.ACM，2005：6-15.

　　[10] BORGELT C.Canonical forms for frequent graph mining[M].Advances in Data Analysis,，Springer Berlin Heidelberg,，2007：337-349.

　　[11] LESKOVEC J.Stanford large network dataset collection[J].URL http：//snap.stanford.edu/data/index.html，2011.