尹虹毅

　?。ㄍ瑵髮W(xué) 電子與信息工程學(xué)院,，上海 201804）

摘要：精神分裂癥是最常見的精神疾病之一，目前具體病因尚未明確,，準(zhǔn)確診斷患病與否是治療該疾病的前提,。深度學(xué)習(xí)是一種構(gòu)造多層神經(jīng)網(wǎng)絡(luò)的機器學(xué)習(xí)方法，具有發(fā)現(xiàn)數(shù)據(jù)中隱藏的分布式特征表示的能力,。針對精神分裂癥患者的腦電信號,，提出了一種棧式自編碼網(wǎng)絡(luò)深度模型，以達到根據(jù)腦電信號自動識別受試者是否患病的效果,。

關(guān)鍵詞：深度學(xué)習(xí); 精神分裂癥,；腦電

0引言

　　精神分裂癥是一種持續(xù)、慢性的精神疾病，臨床上表現(xiàn)為思維,、情感,、行為等多方面精神障礙，是精神病里最常見,、最嚴(yán)重的一種［1］,。精神分裂癥病程多遷延并呈進行性發(fā)展，如果能夠在患病早期準(zhǔn)確診斷,，并給予合理治療,，多數(shù)患者的病情是可以得到控制的,。目前,，科學(xué)家們尚未找出精神分裂癥的具體成因，但研究顯示,，精神分裂癥患者的大腦總體來說與非患者的大腦有區(qū)別［2］,。

　　腦電（Electroencephalogram, EEG）是由腦部神經(jīng)活動產(chǎn)生并且始終存在于中樞系統(tǒng)的自發(fā)性、節(jié)律性的電位活動,。腦電是大腦的活動狀態(tài)的反映,，是幫助診斷大腦疾病的一種輔助檢查方法。人類腦電波由5個主要波段構(gòu)成：delta波(1~3 Hz),、theta波(4~7 Hz),、alpha波(8~13 Hz)、beta波(14~30 Hz)和gamma波(31~50 Hz)［3］,。這5個波段的特征對于精神分裂癥的診斷有著重要的參考價值,。

　　本文提出了一種基于深度學(xué)習(xí)的精神分裂癥患者的腦電分析方法：利用精神分裂癥患者和正常對照者的腦電信號，訓(xùn)練深度神經(jīng)網(wǎng)絡(luò),，使該模型具有根據(jù)輸入腦電信號,，自動判別受試者是否患有精神分裂癥的功能。

1深度學(xué)習(xí)網(wǎng)絡(luò)

　　“機器學(xué)習(xí)”的概念自20世紀(jì)50年代提出以來就備受科技界的關(guān)注,，而近年來“深度學(xué)習(xí)”逐漸成為機器學(xué)習(xí)研究中的一個新的領(lǐng)域［4］,，并在計算機視覺和語音識別方面取得相關(guān)成果。

　　1.1多層特征學(xué)習(xí)

　　深度學(xué)習(xí)網(wǎng)絡(luò)源于人工神經(jīng)網(wǎng)絡(luò),。目前,，大部分機器學(xué)習(xí)算法都屬于淺層學(xué)習(xí)，其局限性表現(xiàn)為對復(fù)雜分類問題圖1深度學(xué)習(xí)網(wǎng)絡(luò)的多層架構(gòu)

　　的泛化能力受到制約,。深度學(xué)習(xí)網(wǎng)絡(luò)提供了一種多層特征學(xué)習(xí)的策略,，即通過學(xué)習(xí)一種多層非線性網(wǎng)絡(luò)結(jié)構(gòu)，實現(xiàn)復(fù)雜函數(shù)逼近,，表征輸入數(shù)據(jù)從低層到高層的不同表示［5］,，其多層架構(gòu)示意圖如圖1所示。

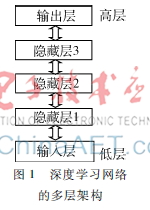
　　這種基于多層特征學(xué)習(xí)的深度結(jié)構(gòu)由一個輸入層、多個隱藏層和一個輸出層構(gòu)成,。該模型的訓(xùn)練分為兩個階段：逐層貪婪訓(xùn)練階段和微調(diào)階段,。在逐層貪婪訓(xùn)練階段，每次只訓(xùn)練網(wǎng)絡(luò)中的一層,，即首先訓(xùn)練一個只含一個隱藏層的網(wǎng)絡(luò),，僅當(dāng)這層網(wǎng)絡(luò)訓(xùn)練結(jié)束之后才開始訓(xùn)練一個有兩個隱藏層的網(wǎng)絡(luò)，以此類推,，直到訓(xùn)練完所有網(wǎng)絡(luò),。在每一步中，把已經(jīng)訓(xùn)練好的前層k-1固定,，即把已經(jīng)訓(xùn)練好的k-1層的輸出作為第k層的輸入,。在微調(diào)階段，這些層單獨訓(xùn)練所得到的權(quán)重被用來初始化最終的深度網(wǎng)絡(luò)的權(quán)重,，然后使用梯度下降算法對網(wǎng)絡(luò)中所有的權(quán)重值進行優(yōu)化,。

　　深度學(xué)習(xí)通過組合低層特征形成更加抽象的高層表示屬性類別或特征，以發(fā)現(xiàn)數(shù)據(jù)中隱藏的分布式特征表示［6］,，這對于復(fù)雜模型的分析具有相當(dāng)重要的作用,。當(dāng)數(shù)據(jù)充足時，該算法可以學(xué)習(xí)到豐富的信息,，故訓(xùn)練的數(shù)據(jù)越多,，其效果越好。因此,，深度學(xué)習(xí)適用于數(shù)據(jù)信息量較大的分析場合,。

　　1.2棧式自編碼網(wǎng)絡(luò)

　　1.2.1自編碼網(wǎng)絡(luò)

　　自編碼神經(jīng)網(wǎng)絡(luò)是一種無監(jiān)督學(xué)習(xí)算法，它通過設(shè)置目標(biāo)值等于輸入值,，來學(xué)習(xí)輸入數(shù)據(jù)的編碼方式,。圖2是一個自編碼神經(jīng)網(wǎng)絡(luò)的示例。

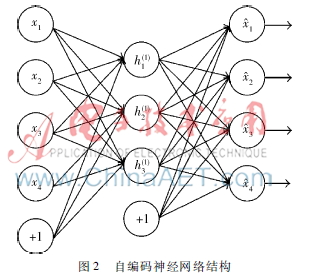
　　假設(shè)有一個固定無標(biāo)簽樣本x(1),…,xm,它包含m個樣例,。對于單個樣例  x,，定義其代價函數(shù)為：

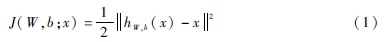
　　其中，W為網(wǎng)絡(luò)的權(quán)重,，b為網(wǎng)絡(luò)的偏差,hW,b(x)為網(wǎng)絡(luò)的輸出,。

　　對于全部樣本，定義整體代價函數(shù)為：

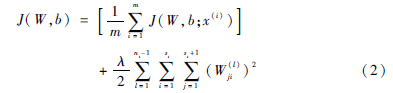
　　其中,，λ為權(quán)重衰減參數(shù),。第一項為每個樣例的代價函數(shù)的平均；第二項為權(quán)重衰減項,，其目的是減小權(quán)重的幅度,，防止過度擬合,。

　　自編碼神經(jīng)網(wǎng)絡(luò)的目標(biāo)是嘗試逼近一個恒等函數(shù)，從而使得輸出hW,b(x)接近于輸入x,。通過在自編碼神經(jīng)網(wǎng)絡(luò)加入某些限制,，可以從輸入數(shù)據(jù)中提取出一些有用的結(jié)構(gòu)。例如,，輸入x是一個100維的數(shù)據(jù),，即m=100,若隱藏層有50個神經(jīng)元，即L2=50,，輸出也是100維的,hW,b(x)∈R100,。由于隱藏層只有50個神經(jīng)元，自編碼神經(jīng)網(wǎng)絡(luò)被迫去學(xué)習(xí)輸入數(shù)據(jù)的壓縮表示,。如果輸入數(shù)據(jù)中隱含著一些特定的結(jié)構(gòu),，比如某些輸入特征是彼此相關(guān)的，那么通過這一算法就可以發(fā)現(xiàn)輸入數(shù)據(jù)中的這些相關(guān)性,。即使在隱藏層神經(jīng)元的數(shù)量較大的情況下,，甚至多于輸入層神經(jīng)元的數(shù)目,，仍可通過給自編碼神經(jīng)網(wǎng)絡(luò)施加一些其他的限制條件,，例如稀疏性限制［7］，來發(fā)現(xiàn)輸入數(shù)據(jù)的結(jié)構(gòu),。

　　1.2.2稀疏性

　　假設(shè)神經(jīng)元的激活函數(shù)是sigmoid函數(shù),，當(dāng)神經(jīng)元的輸出接近于1時認(rèn)為它被激活，而輸出接近于0時認(rèn)為它被抑制,，那么使得神經(jīng)元大部分的時間都處于被抑制狀態(tài)的限制稱為稀疏性限制［8］,。

　　若在給定輸入為x情況下，自編碼神經(jīng)網(wǎng)絡(luò)隱藏神經(jīng)元j的激活度為a(2)j,，則該隱藏神經(jīng)元j在訓(xùn)練集上的平均活躍度為：

　　根據(jù)稀疏性的定義,，限制隱藏神經(jīng)元j的平均活躍度接近于0，即:

　　其中,，ρ是稀疏性參數(shù),，通常取一個接近于0的較小的值。

　　同時,，在代價函數(shù)中加入一個額外的懲罰因子,，懲罰那些ρ∧j和ρ有顯著不同的情況，從而使得隱藏神經(jīng)元的平均活躍度保持在較小范圍內(nèi),。本算法選擇相對熵（KL divergence）,，即懲罰因子:

　　∑s2j=1KL(ρρ∧j)（5）

　　其中，KL(ρρ∧j)=ρlogρρ∧j+(1－ρ)log1－ρ1－ρ∧j是一個以ρ為均值和一個以ρ∧j為均值的兩個伯努利隨機變量之間的相對熵,。

　　在加入了稀疏性限制后,，總體代價函數(shù)可以表示為:

　　Jsparse(W,b)=J(W,b)+β∑s2j=1KL(ρρ∧j)（6）

　　其中，J(W,b)如之前所定義，而β為控制稀疏性懲罰因子的權(quán)重,。

　　1.2.3棧式自編碼算法

　　棧式自編碼網(wǎng)絡(luò)是由多層稀疏自編碼網(wǎng)絡(luò)組成的神經(jīng)網(wǎng)絡(luò),，其前一層自編碼網(wǎng)絡(luò)的輸出作為其后一層自編碼網(wǎng)絡(luò)的輸入［9］。棧式自動編碼網(wǎng)絡(luò)的結(jié)構(gòu)示意圖如圖3所示,。

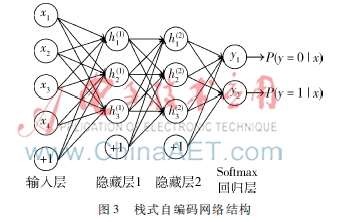
　　棧式自編碼網(wǎng)絡(luò)的訓(xùn)練方法如下：在訓(xùn)練每一層參數(shù)時,，固定其他各層參數(shù)保持不變。在上述預(yù)訓(xùn)練過程完成之后,，進行微調(diào),，即通過反向傳播算法同時調(diào)整所有層的參數(shù)以改善結(jié)果。

　　1.3Softmax回歸

　　Softmax回歸解決的是多類分類問題,，其思想如下：對于給定的測試輸入樣例（x,y）,，利用假設(shè)函數(shù)計算屬于每一個類別j的概率值p(y=j|x)，則該假設(shè)函數(shù)hθ(x)形式如下：

2基于棧式自編碼的精神分裂癥腦電分析

　　2.1數(shù)據(jù)集

　　本文所用數(shù)據(jù)均為醫(yī)院采集的真實數(shù)據(jù),，其中有62個精神分裂癥患者,，88個健康對照者。被試者的EEG信號均在靜息閉眼的狀態(tài)下采集,。EEG的信號使用含有 64 個導(dǎo)聯(lián)的放大器進行數(shù)據(jù)的采集,，采樣頻率為1 000 Hz，所采集的樣本數(shù)據(jù)都包含64個導(dǎo)聯(lián)上2~3 min的時域數(shù)據(jù),。

　　2.2腦電特征提取

　　因為精神分裂癥是由于大腦異常引起的,，在得到的64個導(dǎo)聯(lián)的信號中，選取了59個最能直接反映大腦活動狀態(tài)的導(dǎo)聯(lián),，分別是AF3,、AF4、AF7,、AF8,、C1、C2,、C3,、C4、C5,、C6,、CP1、CP2,、CP3,、CP4、CP5,、CP6,、CPz,、Cz、F1,、F2,、F3、F4,、F5,、F6、F7,、F8,、FC1、FC2,、FC3,、FC4、FC5,、FC6,、Fp1、Fp2,、Fpz,、FT7、FT8,、Fz,、O1,、O2,、Oz、P1,、P2,、P3、P4,、P5,、P6、P7,、P8,、PO3、PO4,、PO7,、PO8、POz,、Pz,、T7,、T8、TP7,、TP8,。

　　由于深度學(xué)習(xí)網(wǎng)絡(luò)需要大量訓(xùn)練樣本，在此,，對每個人的時域數(shù)據(jù)進行截取多個時間片段樣本的處理,，將每個時域數(shù)據(jù)截成長度為2 s、重疊為25%的多個片段樣本,。通過這樣處理后,，獲得8 709個精神分裂癥患者的時間片段，11 542個健康對照者的時間片段樣本,。

　　對每個樣本,，采用快速傅里葉變換獲取其功率譜密度。接著,，提取其在頻域中5個頻帶的能量作為特征,，即delta波段(1~3 Hz)、theta波段(4~7 Hz),、alpha波段(8~13 Hz),、beta波段(14~30 Hz)和gamma波段 (31~50 Hz)的能量。最后,，每個樣本提取到295個特征,，作為棧式自編碼網(wǎng)絡(luò)的輸入。

　　2.3棧式自編碼網(wǎng)絡(luò)的實現(xiàn)

　　本文提出的用于精神分裂癥腦電分析的棧式自編碼網(wǎng)絡(luò)由多個自編碼網(wǎng)絡(luò)和一個Softmax回歸層構(gòu)成,。在完成訓(xùn)練后,，這個棧式自編碼網(wǎng)絡(luò)能夠根據(jù)測試腦電信號實現(xiàn)自動判別該腦電所屬實驗者是否患有精神分裂癥。

　　這個棧式自編碼網(wǎng)絡(luò)首先對網(wǎng)絡(luò)中的每層到進行逐層貪婪訓(xùn)練：輸入的數(shù)據(jù)（295個頻域能量特征）被用于訓(xùn)練第一個稀疏自編碼網(wǎng)絡(luò),，以獲取輸入數(shù)據(jù)的初級特征h(1),。在此，使用梯度下降方法來最優(yōu)化代價函數(shù),，從而學(xué)習(xí)出第一個網(wǎng)絡(luò)的最佳權(quán)重參數(shù),。

　　在最佳權(quán)重學(xué)習(xí)完畢后，使用輸入數(shù)據(jù)在第一個網(wǎng)絡(luò)進行前向傳播,，得到輸入數(shù)據(jù)的初級特征h(1),。而第一個網(wǎng)絡(luò)得到的特征h(1)被用作第二個網(wǎng)絡(luò)的輸入，采用同樣的方法獲取第二個網(wǎng)絡(luò)的特征h(2),。將前一層網(wǎng)絡(luò)學(xué)習(xí)到的特征作為下一層網(wǎng)絡(luò)的輸入,，循環(huán)以上步驟，可獲得每層網(wǎng)絡(luò)的最佳權(quán)重參數(shù),。最后一層隱藏層的特征h(n-1)被用作Softmax回歸層的輸入,，以獲取其最佳權(quán)重參數(shù),。

　　在完成了逐層最佳權(quán)重參數(shù)學(xué)習(xí)后，對整個網(wǎng)絡(luò)進行微調(diào),，以獲得最佳全局權(quán)重,。

3實驗分析

　　本實驗將從兩個方面進行分析。為探究隱藏層節(jié)點數(shù)對識別效果的影響,，先探究只含有一個隱藏層的自編碼網(wǎng)絡(luò)的隱藏層節(jié)點數(shù)對識別效果的影響,，之后再探究棧式自編碼網(wǎng)絡(luò)的隱藏層層數(shù)對識別效果的影響。

　　3.1單層網(wǎng)絡(luò)隱藏層節(jié)點數(shù)對實驗結(jié)果的影響

　　首先構(gòu)造了一個輸入層含有295個節(jié)點,、輸出層為2個節(jié)點Softmax回歸層的單隱藏層自編碼網(wǎng)絡(luò),，令其隱藏層節(jié)點數(shù)為10~1 000，以觀察隱藏層節(jié)點數(shù)對精神分裂癥腦電的識別率,，實驗結(jié)果如圖4所示,。

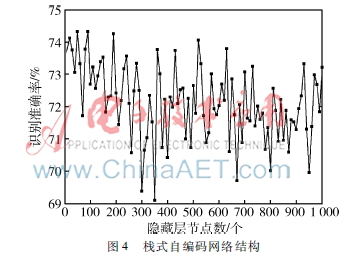
　　從圖4可以看到，采用了稀疏自編碼網(wǎng)絡(luò)對精神分裂癥腦電具有較好的識別效果,，不同隱藏層節(jié)點所獲得的識別準(zhǔn)確率均在72%左右,，其中當(dāng)隱藏層節(jié)點數(shù)為80、110,、200時,，識別率最高，超過了74%,。

　　3.2網(wǎng)絡(luò)層數(shù)對實驗結(jié)果影響

　　為探究棧式自編碼網(wǎng)絡(luò)的隱藏層層數(shù)對識別效果的影響,，分別構(gòu)造了隱藏層層數(shù)為2層、3層和4層的棧式自編碼網(wǎng)絡(luò),，具體網(wǎng)絡(luò)參數(shù)和實驗結(jié)果如表1所示,。

　　從表1結(jié)果可以看到，當(dāng)隱藏層數(shù)目增加時,，該棧式自編碼網(wǎng)絡(luò)對精神分裂癥腦電的識別率有小幅度的提升,。

4結(jié)論

　　針對精神分裂癥難以診斷的問題，本文提出了利用深度神經(jīng)網(wǎng)絡(luò)對精神分裂癥腦電進行分析判別的方法,。該方法通過建立含有多個隱層結(jié)構(gòu)的棧式自編碼網(wǎng)絡(luò)，從大量腦電數(shù)據(jù)中獲取隱含結(jié)構(gòu)信息,，以提高分類識別以及預(yù)測的準(zhǔn)確性,。實驗驗證了所提出的方法的有效性，對 62個精神分裂癥患者和88個健康對照者的腦電數(shù)據(jù)的識別準(zhǔn)確率較高,，且有較好的適應(yīng)性,。從實驗分析可得，實驗結(jié)果與理論分析基本相符,。

　　在未來的研究中,，要解決的主要問題有:（1）深度神經(jīng)網(wǎng)絡(luò)層數(shù)的極限在哪里,，是否存在某個固定的層數(shù)使得該網(wǎng)絡(luò)達到性能最優(yōu)；（2）如何決定某類問題深度學(xué)習(xí)的層數(shù)和隱藏層節(jié)點的個數(shù),。

參考文獻

　?。?］ 管麗麗,杜立哲,馬弘. 精神分裂癥的疾病負(fù)擔(dān)(綜述)［J］. 中國心理衛(wèi)生雜志,2012,26(12):913919.

　　［2］ 宋安林. 精神分裂癥腦組織各部位神經(jīng)病理改變對比研究［D］.重慶：重慶醫(yī)科大學(xué),2010.

　?。?］ TEPLAN M. Fundamentals of EEG measurement ［J］. Measurement Science Review, 2002, 2(2): 110.

　?。?］ YOSHUA B, COURVILLE A, VINCENT P. Representation learning: a review and new perspectives［J］.IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013,35(8):17981828.

　　［5］ SCHLKOPF B, PLATT J,HOFMANN T. Greedy layerwise training of deep networks［J］. Advances in Neural Information Processing Systems,，2007,，19：153160.

　　［6］ HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks［J］. Science,， 2006,，313（5786）:504507.

　　［7］ OLSHAUSEN B A, FIELD D J. Sparse coding with an overcomplete basis set: a strategy employed by VI?［J］. Vision Research,，1997,，37（23）: 33113326.

　　［8］ LEE H,， BATTLE A,， RAINA R， et al. Efficient sparse coding algorithms［C］.  Conference on Neural Information Processing Systems, 2007:801808.

　?。?］ YOSHUA B, DELALLEAU O. On the expressive power of deep architectures［C］. Interrational Couference on Discovery Science,2011,6925:1836.