董博1,，王雪2
（1. 遼寧大學(xué) 計(jì)算中心,，遼寧 沈陽 110036,；2. 遼寧大學(xué) 信息化中心，遼寧 沈陽 110036）
摘要：針對網(wǎng)絡(luò)安全威脅問題,，將人工智能理論和相關(guān)技術(shù)與網(wǎng)絡(luò)安全態(tài)勢評估相融合,，提出一種以細(xì)化變量進(jìn)行分組的貝葉斯網(wǎng)絡(luò)作為基礎(chǔ)研究的網(wǎng)絡(luò)安全態(tài)勢評估方法。該算法可以有效減少變量數(shù)量,，縮短產(chǎn)生貝葉斯網(wǎng)絡(luò)的程序運(yùn)行時間,，并通過相關(guān)實(shí)驗(yàn)驗(yàn)證了有效地減少變量數(shù)量對最終的結(jié)果并沒有產(chǎn)生過多影響。用本算法對大量網(wǎng)絡(luò)實(shí)際運(yùn)行數(shù)據(jù)進(jìn)行測試,，結(jié)果表明該方法能夠很好地區(qū)分不同的網(wǎng)絡(luò)安全威脅,，從而能夠有效評估網(wǎng)絡(luò)安全態(tài)勢。
關(guān)鍵詞：貝葉斯網(wǎng)絡(luò),；網(wǎng)絡(luò)安全,；態(tài)勢評估；結(jié)構(gòu)學(xué)習(xí)
0引言
網(wǎng)絡(luò)安全態(tài)勢感知就是把所收集的與網(wǎng)絡(luò)安全相關(guān)的要素進(jìn)行融合,，然后按照一定的方法對這些要素進(jìn)行分析和理解,，進(jìn)而判斷當(dāng)前網(wǎng)絡(luò)的安全態(tài)勢并預(yù)測未來的安全態(tài)勢,。
1網(wǎng)絡(luò)安全態(tài)勢評估方法
網(wǎng)絡(luò)安全態(tài)勢評估是網(wǎng)絡(luò)安全態(tài)勢感知的重要環(huán)節(jié)，國內(nèi)外學(xué)者從不同的角度出發(fā),，對網(wǎng)絡(luò)安全態(tài)勢評估做了大量科學(xué)研究工作,。
在國內(nèi)，韋勇等［1］證明了基于多源融合網(wǎng)絡(luò)安全態(tài)勢評估比基于單源網(wǎng)絡(luò)安全態(tài)勢評估更加準(zhǔn)確有效,。劉念等［2］提出一種基于免疫的網(wǎng)絡(luò)安全態(tài)勢感知方法,。
在國外,，Mohsen Naderpour等［3］提出基于SA支持系統(tǒng)的GDTA方法,，這種方法能幫助管理人員找出異常情況。Jason shifnet 等開發(fā)了Spinning Cube of Potential Doom 系統(tǒng),， 極大地提高了網(wǎng)絡(luò)安全態(tài)勢評估能力［4］,。
2貝葉斯網(wǎng)絡(luò)
貝葉斯網(wǎng)絡(luò)是描述數(shù)據(jù)變量之間依賴關(guān)系的圖形模型 ,其描述如下：網(wǎng)絡(luò)結(jié)構(gòu)S=(G,Θ)是一個有向圖 ,其中，每一個節(jié)點(diǎn)代表一個數(shù)據(jù)變量,，G=(X,E) 是沒有環(huán)路沒有頂點(diǎn)的圖,，X={X1,...,Xn}。Θ={P(Xi|Pa(Xi))}為其中Xi節(jié)點(diǎn)在其父節(jié)點(diǎn)的條件概率集合,。
用P(Xi)代表節(jié)點(diǎn)Xi的條件概率密度,，Pa(Xi)表示其父節(jié)點(diǎn)集合,由貝葉斯推理公式有：
P(Xi)=P(Xi|Pa(Xi))(1)
根據(jù)概率鏈規(guī)則,由n個變量決定的聯(lián)合貝葉斯概率為：
P(x1,x2,...,xn)=∏ni=1p(xi|Pa(xi))(2)
在S中不存在任何有向環(huán), 稱為有向無環(huán)圖(Directed Acyclic graph , DAG) 。參考文獻(xiàn)［5］中描述了有向無環(huán)圖的遞推公式：
r(n)=∑ni=1(－1)i+1n
i2i(n－1)r(n－i)=n2O(π)(3)
其中,，r(1)=1, r(2)=3, r(3)=25, r(5)=29 281, r(10)=4.2×1018,，這意味著，一旦節(jié)點(diǎn)數(shù)大于7,，對所有節(jié)點(diǎn)在有效時間內(nèi)執(zhí)行一次完全遍歷是不可能的,。
3聚類算法理論框架和研究方法
由于在構(gòu)建貝葉斯網(wǎng)絡(luò)的過程中，網(wǎng)絡(luò)的結(jié)構(gòu)復(fù)雜性使得變量的數(shù)目過多,，造成表達(dá)式超指數(shù)的增長,。為了解決這個問題，本文采用一種新的聚類算法,，采用細(xì)分變量作為子集（或群組）,，通過單獨(dú)地學(xué)習(xí)每一個子集的結(jié)構(gòu)，由這些子集的結(jié)構(gòu)最終組裝成最終的結(jié)構(gòu),。
3.1理論背景
以下用到的Robinson 公式［5］表明有向無環(huán)圖中變量數(shù)量,。其中，n表示變量的數(shù)量,，r(1)=1,。
r(n)=∑ni=1(－1)i+12i(n－i)n
ir(n－i)(4)
r(n)>∑kl=1r(Jl+1)(5)
其中，J1+J2+…+Jk=n-1,，Jl+1<n,， l=1,2,…,k。
定理1
對于n≥2，有：
r(n)≥2n-2nr(n-1)
r(n)≥2(n-1-J)(n+J-2)2n(n-1)...(J+2)×r(J+1)(6)
其中,，0≦J≦n-1,。
當(dāng)n=2時，r(2)=3≧2,。當(dāng)n>2時,，參考文獻(xiàn)［2］中已經(jīng)證明定理成立。
定理2
r(n)∑kl=1r(Jl+1)≥p(n,Jk－Jk+,k)1(7)
證明：
由定理1中公式(6)：
r(n)≥2(n－1－Jl)(n+Jl－2)2n(n－1)...(Jl+2)×r(Jl+1)
l=1,...,k
所以：
∑kl=1r(n)≥2(n－1－Jl)(n+Jl－2)2n(n－1)...(Jl+2)r(Jl+1)（8）
k×r(n)≥∑kl=12(n－1－(Jk+）)(n+(Jk－）－2)2n(n－1)...(Jk++2)r(Jl+1)(9)
由于上式中,，2（n－1－(Jk+))(n+(Jk－－2)2n(n－1)...(Jk++2)是常數(shù),，與l無關(guān)，即:
k×r(n)≥2(n－1－(Jk+）)(n+(Jk－）－2)2n(n－1)...(Jk++2)∑kl=1r(Jl+1)(10)
因此:
r(n)∑kl=1r(Jl+1)≥2(n－1－(Jk+）)(n+(Jk－）－2)2n(n－1)...(Jk++2)k(11)
即:
r(n)∑kl=1r(Jl+1)≥p(n,Jk－Jk+,k)1(12)
所以：
r(n)>∑kl=1r(Jl+1)(13)
例如,，存在20個變量分成四個子集,，子集1中包含5個變量，子集2中包含3個變量,，子集3中包含6個變量,，子集4中包含6個變量。則有：
r(n)=658.114×∑kl=1r(Jl+1)∑kl=1r(Jl+1)(14)
表明r(n)遠(yuǎn)大于∑kl=1r(Jl+1),。
貝葉斯網(wǎng)絡(luò)學(xué)習(xí)過程的主要目的是在相應(yīng)變量間進(jìn)行推理,，得出有效的因果關(guān)系，從而形成一個有向無環(huán)圖,。對所有的變量（包括興趣變量）進(jìn)行結(jié)構(gòu)學(xué)習(xí),。最終的結(jié)構(gòu)學(xué)習(xí)過程如算法1。
算法1貝葉斯分組學(xué)習(xí)優(yōu)化算法
定義：n:分組數(shù)量
λi:分組的索引
Vij:在λi分組下的變量j索引
P(Vij): Vij的父集
N: 類的變量節(jié)點(diǎn)
STi:分組i的變量結(jié)構(gòu)
Oi:分組變量排序
Nλi:屬于λi分組內(nèi)的變量數(shù)量
Vλi: i分組的變量集
算法過程如下:
1：Begin
2：For each i<=n Do Oi←MWST(N, Vλi:)
3：End for
5：For each i<=n Do STi←K2(Oi, Vλi:)
6:End For
7:For each 2<=i<=n do Vλi←VλiUVλi\\{N}
8:For each 1<= j<= Nλi do
9:從STi中開始,，添加到ST1中并保留從
10:Vij和P(Vij)之間的弧
11:End For
12: End For
很多學(xué)者提出了多種關(guān)于貝葉斯網(wǎng)絡(luò)的結(jié)構(gòu)學(xué)習(xí)算法,，比如MWST算法、TPDA（Three Phase Dependency Analysis)算法,、K2算法,、ACOB (Ant Colony OptimizationB algorithm)等。本文選用K2算法進(jìn)行對比分析的主要原因是K2算法的計(jì)算時間短,，算法復(fù)雜度低,，穩(wěn)定度高。為了解決初始變量有序化問題,，采用了MWST算法,。MWST算法對數(shù)據(jù)集大小的變化不太敏感，并能產(chǎn)生初始化序列,，而且其產(chǎn)生的圖與之前的圖差別不大,。因此，采用MWST算法既能滿足初始化序列的要求又能非常準(zhǔn)確地接近原始數(shù)據(jù),，可以成為K2算法的有效輸入,。
4實(shí)驗(yàn)過程與結(jié)果
選用了BNT toolbox工具包和Matlab2014b實(shí)驗(yàn)平臺,，實(shí)現(xiàn)MWST算法和K2算法的結(jié)構(gòu)學(xué)習(xí)過程。
運(yùn)行環(huán)境為：Inter Core2 2.8GHz處理器,，4 GB內(nèi)存,，Win7 64位操作系統(tǒng)，系統(tǒng)平均CPU利用率為38%,，內(nèi)存的平均使用率為17%,。
數(shù)據(jù)來源采用美國林肯實(shí)驗(yàn)室的數(shù)據(jù)KDDCUP，其包含連續(xù)屬性及離散屬性等不同屬性值(如攻擊持續(xù)時間,、網(wǎng)絡(luò)協(xié)議類型等),，并標(biāo)有其所屬的類型(如正常或具體的攻擊類型) ,。所有攻擊主要分為以下4大類：
?。?)DoS(Denial of Service Attacks )：拒絕服務(wù)。
?。?)UToR(User to Root Attacks)：試圖獲取根用戶權(quán)限。
?。?)RToL(Remote to Local User Attacks)：入侵者試圖利用系統(tǒng)的缺陷繞過防火墻,。
（4)Probe（Probe in network）：端口掃描,。
4.1Kmeans算法數(shù)據(jù)預(yù)處理
設(shè)定聚類范圍為 2～10,，采用層次聚類算法和自舉技術(shù)優(yōu)化的K2算法進(jìn)行聚類，得到每個因素的聚類準(zhǔn)則值,，如圖1所示,。找到最佳聚類數(shù)和聚類中心可以使每個屬性更好地反映數(shù)據(jù)特性，避免由專家指定而造圖1各屬性聚類準(zhǔn)則值
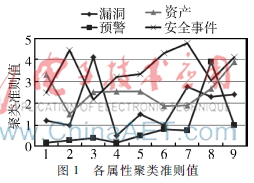
成的主觀影響,。同理適用于其他影響因素,，得到其最佳聚類數(shù)和聚類中心如表1所示。
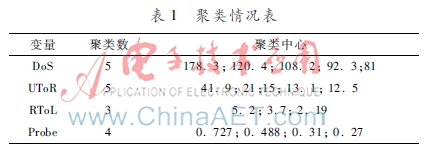
4.2實(shí)驗(yàn)具體過程
(1)選取10%的數(shù)據(jù)集（共 494 019 條連接記錄）作為樣本訓(xùn)練數(shù)據(jù)集,。之后獲取來自于本校的防火墻日志,，使用20150104 00:00:00 到20150107 23:59:59之間，合計(jì)四天共96 h的數(shù)據(jù),，共875個報警事件作為測試集,。
（2)對訓(xùn)練集中連續(xù)性屬性進(jìn)行離散化處理,，確保其中屬性數(shù)據(jù)值在 100 個左右,，并在此基礎(chǔ)上進(jìn)行分組貝葉斯算法的分類試驗(yàn)。
?。?)分別用本文提出的算法和經(jīng)典的K2算法分別獲取100個變量和1 024個變量,。
?。?)對數(shù)據(jù)進(jìn)行歸類，按照相關(guān)試驗(yàn)類型的不同預(yù)歸類成2 類或5個主要類,。
?。?)分兩種情況對算法進(jìn)行比較：
①數(shù)據(jù)記錄只分類成正常(Normal)或異常(Unnormal)兩類,，即將所有具體類型的攻擊都作為異常類,。
②數(shù)據(jù)記錄分類成 5大類 (Normal,、DoS,、UToR、RToL,、Probe),，各具體攻擊類型分別歸類到這5類中。
4.3實(shí)驗(yàn)結(jié)果和分析
在第一階段實(shí)驗(yàn)過程中,，分別用K2算法和本文設(shè)計(jì)的算法對不同的數(shù)據(jù)集進(jìn)行運(yùn)算,。可以看出,，與經(jīng)典的K2算法相比,，本文算法運(yùn)行時間得到了有效的縮短。在第二階段實(shí)驗(yàn)中,，驗(yàn)證了分組變量對實(shí)驗(yàn)結(jié)果的影響微乎其微,，如表2所示。其中訓(xùn)練集數(shù)據(jù)分別含有100個變量和1 024個變量,。
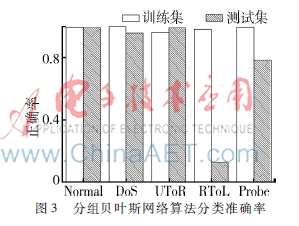
對于算法有效性的評價標(biāo)準(zhǔn)采用分類準(zhǔn)確率來衡量,。采取兩種情形進(jìn)行試驗(yàn)，第一種情形將數(shù)據(jù)的類型分成兩種如表3所示,，可以看出本文算法分類準(zhǔn)確度明顯優(yōu)于K2算法,。第二種情形將數(shù)據(jù)分成5類，結(jié)果如圖2和圖3表3分類準(zhǔn)確率(%)類型訓(xùn)練集測試集本文,。
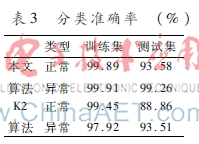
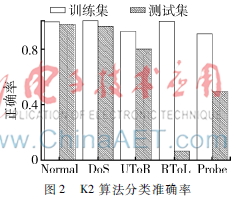
從圖2和圖3可以看出,，本文所提算法在準(zhǔn)確率方面也優(yōu)于K2算法。但無論是本文方法還是傳統(tǒng)的K2算法,，在UToR與RToL訓(xùn)練樣本的分類準(zhǔn)確度上,，還都達(dá)不到較好的效果，主要原因是這兩種訓(xùn)練樣本占整體樣本比例相對較少,。當(dāng)訓(xùn)練樣本的數(shù)量較多時,，分類的準(zhǔn)確率會得到較大提升。
5結(jié)束語
首先,，本文在數(shù)學(xué)上證明了通過對相關(guān)變量進(jìn)行分組并形成相關(guān)的聚類可以有效地減少貝葉斯網(wǎng)絡(luò)的規(guī)模,。其次,，選取了Kmeans方法優(yōu)化了聚類過程。最后,，通過實(shí)驗(yàn)證明本文方法可以大量減少網(wǎng)絡(luò)態(tài)勢分析中的變量數(shù)量,，并且丟失的數(shù)據(jù)在實(shí)際評估過程中不影響推理過程所產(chǎn)生的貝葉斯網(wǎng)絡(luò)，同時節(jié)省了大量的程序執(zhí)行時間,。
參考文獻(xiàn)
?。?］ 韋勇，連一峰,，馮登國． 基于信息融合的網(wǎng)絡(luò)安全態(tài)勢評估模型［J］．計(jì)算機(jī)研究與發(fā)展,， 2009， 46(3):353362.
?。?］ 劉念,劉孫俊,劉勇,等.一種基于免疫的網(wǎng)絡(luò)安全態(tài)勢感知方法［J］. 計(jì)算機(jī)科學(xué), 2010,37(1):126129.［3］ NADERPOUR M, LU J, ZHANG G. An intelligent situation awareness support system for safetycritical environments［J］. Decision Support Systems, 2014,59(1):325340.
?。?］ STEPHEN L.The spinning cube of potential doom［J］. Communications ACM,2004, 47(6): 2526．
［5］ ROBINSON R W. Counting unlabeled acyclic digraphs［C］.In: Lecture Notes in Mathematics, Combinatorial Mathematics, 1977:2843.