董振華,李喜艷

　　(鄭州成功財(cái)經(jīng)學(xué)院,河南 鞏義 451200)

       摘要：數(shù)字圖像信息隱藏算法要求高的魯棒性和透明性,，通過分析矩陣運(yùn)算的特征，提出改進(jìn)的EMD-S算法,。將秘密信息通過S盒的壓縮變換,，嵌入到分解圖像的最大奇異值當(dāng)中。通過實(shí)驗(yàn)表明,，本文算法能夠較好地抵抗JPEG壓縮,，具有較大的數(shù)據(jù)嵌入率和較好的魯棒性,。

　　關(guān)鍵詞：信息隱藏；矩陣運(yùn)算,；奇異值分解,；魯棒性

0引言

　　數(shù)字圖像信息隱藏是信息隱藏的一個重要分支，數(shù)字圖像信息隱藏技術(shù)主要是通過分析圖像的本質(zhì)特征,，嵌入秘密信息,，使人類從視覺上感覺不到圖像的改變，從而解決數(shù)字圖像的隱蔽通信［1 2］,。參考文獻(xiàn)［3］提出的EMDlike隱藏算法在像素塊的平均值上嵌入秘密信息,，算法的魯棒性得到了一定的提高，但秘密信息直接嵌入在圖像空域的像素中,，嵌入失真較大,，而且魯棒性仍不能滿足實(shí)際需求。參考文獻(xiàn)［4］,、［5］提出SVD和EMD結(jié)合的隱藏算法,，通過在像素塊的奇異值上嵌入秘密信息，提高了載密圖像的質(zhì)量,，并且提高了算法的魯棒性,，但它是以嵌入容量為代價(jià)的。參考文獻(xiàn)［6］提出基于矩陣運(yùn)算的二維EMD算法,，利用矩陣運(yùn)算將秘密信息編碼后分別嵌入在載體像素矩陣的列向量和行向量中,，仿真實(shí)驗(yàn)證明嵌入率較高,，但是該方法也是以犧牲嵌入效率與PSNR值為代價(jià)的,。

　　EMD編碼算法是一種數(shù)字圖像信息隱藏算法，當(dāng)在圖像的n個像素載體中嵌入秘密信息時,，最多只需修改1 bit,。EMD編碼方法的優(yōu)點(diǎn)在于能夠以比較小的修改量獲取較高的嵌入率，并且減小了嵌入引起的失真,，但是EMD編碼方法的魯棒性較差,，當(dāng)圖像發(fā)生微小改動時，有可能會造成秘密信息的不正確提取,。圖像的奇異值具有很好的穩(wěn)定性,，本文充分利用EMD編碼的較高嵌入率和奇異值分解的穩(wěn)定性，并且引入S盒的壓縮變換,，進(jìn)一步提高了數(shù)據(jù)的嵌入率,，提出了SVD和EMD-S結(jié)合的隱藏算法。

1EMD-S編碼算法

　　1.1S盒變換

　　在對稱秘密體制中,，DES算法是一種經(jīng)典的對稱密碼算法,，除了S盒是非線性變換外,，其余都是線性變換。因此,，S盒是DES算法的關(guān)鍵,，任意改變S盒輸入中的幾位，其輸出至少有兩位發(fā)生變化,。

　　每個S盒有4行16列,，以某數(shù)據(jù)流的6 bit數(shù)據(jù)為例，假設(shè)Bj=b1b2b3b4b5b6,，設(shè)b1b6和b2b3b4b5對應(yīng)的十進(jìn)制分別為r和c,，則Sj盒中的r行c列對應(yīng)的十進(jìn)制整數(shù)就是Sj的輸出。例如B1=100111,，從圖1所示的S1盒中查得,，3行3列的十進(jìn)制整數(shù)為2，則S1的輸出為0010,。也就是說,，實(shí)際需要嵌入的信息量為6 bit，經(jīng)過S盒壓縮變換后信息量減少為4 bit,，從而可以更好地保證圖像信息隱藏的魯棒性和不可感知性,。

　　1.2EMD-S算法的實(shí)現(xiàn)

　　EMD編碼算法是一種數(shù)字圖像信息隱藏算法，當(dāng)在圖像的n個像素載體中嵌入秘密信息時,，最多只需修改1 bit,。EMD編碼方法的優(yōu)點(diǎn)在于能夠以比較小的修改量獲取較高的嵌入率，并且減小了嵌入引起的失真,。本文進(jìn)一步提高數(shù)字圖像的信息嵌入率,，提出EMDS編碼算法，在秘密信息嵌入前經(jīng)過S盒的壓縮變換,，然后再嵌入數(shù)字圖像載體中,。EMD-S算法的嵌入步驟如下：

　　(1)假設(shè)秘密信息d=(d1,d2,…,d8)，其中di為6 bit的數(shù)據(jù)流,。將di經(jīng)過Si盒壓縮變換為4 bit的數(shù)據(jù)流,，因?yàn)镋MD編碼嵌入的是2n+1進(jìn)制的數(shù)，所以在這里將4 bit的數(shù)據(jù)流高位補(bǔ)0,，生成5 bit的數(shù)據(jù)流,。經(jīng)過S盒壓縮變換和高位補(bǔ)0操作，形成秘密信息d′=(d1′,d2′,…,d8′),，由原來的48 bit變?yōu)?0 bit的秘密嵌入信息,。

　　(2)把數(shù)字載體圖像分為連續(xù)的大小為2×2的像素組g1,g2,…,gn。

　　(3)計(jì)算權(quán)值函數(shù)f=f(g1,g2,…,gn)=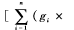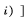×i(mod2n+1)(1)

    (4)差值計(jì)算

　　若S的值為0,，則像素值不進(jìn)行修改,；若S的值不為圖2信息嵌入算法流程0,，且k<=n(k代表第k個秘密比特值，可取0,，1,，…，n),，像素組中g(shù)s=gs+1,，否則像素組中g(shù)2n+1-k=g2n+1-k-1。

　　通過以上4個步驟的操作,，將像素組修改為新的像素值g′1,g′2,…,g′n,，由EMD-S編碼算法的嵌入原理可得嵌入后的像素組滿足公式(3)：

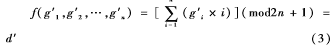
       因此通過公式(3)可以求出秘密信息d′，秘密信息d′通過查詢相應(yīng)S盒可以獲得擴(kuò)展之后的秘密信息d,。通過S1盒可知,，同一個十進(jìn)制數(shù)值對應(yīng)若干個行號和列號組，為了增加信息的嵌入量,，選擇S1盒當(dāng)中最大的一位十進(jìn)制數(shù),。

2SVD和EMD-S結(jié)合的隱藏算法

　　在對矩陣進(jìn)行數(shù)值分解的眾多分析方法中奇異值分解是其中一個典型的方法，因?yàn)槟軌蚝芎玫亟鉀Q逆矩陣問題和矩陣的特征值問題,，而被廣泛應(yīng)用于通信和圖像等領(lǐng)域,。

　　2.1奇異值分解及特性分析

　　奇異值分解(SVD)是一種將矩陣進(jìn)行對角化的數(shù)值算法，從線性代數(shù)的角度,，一幅灰度圖像可以看成是一個非負(fù)矩陣,。若一幅圖像用A表示，定義為A∈RΜ×Ν,，其中,，R表示實(shí)數(shù)域，則矩陣A的奇異值分解定義為A=USVT式中,，U∈RΜ×Ν與V∈RN×N都是正交矩陣,，矩陣S是一個對角矩陣,，對角線上的元素叫做A的奇異值且滿足:σ1≥σ2≥…≥σi≥…≥σM≥0,，分解式USVT稱作A的奇異值分解。奇異值所表現(xiàn)的是圖像的內(nèi)蘊(yùn)特性,，在對圖像做奇異值分解所得的奇異值序列σi中,，第一個奇異值比其他奇異值大得多，圖像奇異值的穩(wěn)定性非常好,，在圖像被施加小的擾動時,，其奇異值不會有大的變化。塊奇異值分解會產(chǎn)生更多具有較大數(shù)值的奇異值,，有利于水印嵌入,。奇異值的這些特性,，保證了水印嵌入的可行性、不可見性以及很好的魯棒性,。本文充分利用奇異值的較好的魯棒性特征,，結(jié)合了EMD-S算法，將兩個算法的優(yōu)點(diǎn)結(jié)合起來,。在EMD-S編碼算法的基礎(chǔ)上使用奇異值分解來提取特征點(diǎn),，不僅保證了圖像可以嵌入較大容量的秘密信息，而且還保證了圖像良好的魯棒性,。

　　2.2信息嵌入過程

　　使用矩陣A表示載體圖像,，嵌入秘密信息d=(d1,d2,…,d8)，其中di為6 bit的數(shù)據(jù)流,。為保證算法具有較大的嵌入容量,，將每一組數(shù)據(jù)流經(jīng)過對應(yīng)的S盒壓縮變換為4 bit的數(shù)據(jù)流。為了更好地應(yīng)用EMD算法,，每組數(shù)據(jù)流的高位補(bǔ)0,，形成5 bit的數(shù)據(jù)流。與此同時對圖像矩陣A進(jìn)行分塊,，對每一個子塊進(jìn)行奇異值分解,，提取出奇異值向量。將秘密信息d′=(d1′,d2′,…,d8′)嵌入到每個子塊的最大奇異值中,。以兩個像素點(diǎn)為一個單位時算法的容量最大,，因此本文算法選取兩個圖像塊的最大奇異值作為嵌入單位。信息嵌入算法流程圖如圖2所示,。

　　具體的嵌入步驟如下：

　　(1)將載體圖像A進(jìn)行分塊,，每塊為2×2，塊與塊之間相互不重疊,；(2)對每個子塊進(jìn)行奇異值分解,，獲取每個子塊的最大奇異值；(3)以相鄰兩個子塊的最大奇異值作為參數(shù),，計(jì)算函數(shù)f

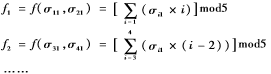
　　(4)秘密信息d′轉(zhuǎn)化為五進(jìn)制的比特流,，并計(jì)算機(jī)差值Si=(di-fi)mod5，根據(jù)EMD-S編碼算法中的修改規(guī)則,，一次修改每個奇異值數(shù)組,。

　　(5)將修改后的奇異值向量(σ′i1,σ′i2)進(jìn)行奇異值逆變換得到新的2×2矩陣，各個子塊組合成新的載有秘密信息的圖像矩陣A′,。

　　2.3信息提取過程

　　在這里使用矩陣A′表示載有秘密信息的圖像,，具體的提取步驟如下：

　　(1) 將載體圖像A′進(jìn)行分塊，每塊為2×2，塊與塊之間相互不重疊,；(2)對每個子塊進(jìn)行奇異值分解,，獲取每個子塊的最大奇異值σ′i1；(3)根據(jù)EMD-S算法,，以兩個奇異值為一個單位進(jìn)行計(jì)算,，獲得權(quán)重函數(shù)f的取值。秘密信息的提取公式如：

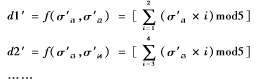
　　(4)秘密信息d′=(d1′,d2′,…,d8′)分別經(jīng)過對應(yīng)S盒的變換,，選擇矩陣中最大的二進(jìn)制數(shù)據(jù)分別得到6 bit的數(shù)據(jù)流d=(d1,d2,…,d8),。

3性能分析與比較

　　3.1性能分析

　　矩陣運(yùn)算方便、直觀,，奇異值分解魯棒性較好,，本文提出改進(jìn)的EMD-S編碼算法，不僅保證了數(shù)據(jù)的嵌入量的增加,，而且為了保證秘密信息的正確提取,，采用奇異值分解的方法對圖像進(jìn)行子塊分解，提高圖像的魯棒性,。本文主要是在文獻(xiàn)［4］的基礎(chǔ)上做的改進(jìn),，在秘密信息嵌入之前先經(jīng)過S盒的壓縮變換，增加了數(shù)據(jù)的嵌入率,，使用奇異值分解,，將秘密信息嵌入到圖像子塊當(dāng)中，同時也保證了圖像的魯棒性,。通過上述理論的分析可得,，本文算法的嵌入率是文獻(xiàn)［4］嵌入率的1.2倍左右。本文參照文獻(xiàn)［4］使用峰值信噪比PSNR來衡量嵌入秘密信息的失真度,，采用位錯率來作為算法魯棒性的客觀評價(jià)標(biāo)準(zhǔn),。但是，每個S盒有連續(xù)的64個整數(shù),，增加了空間復(fù)雜度,。

　　3.2性能比較

　　對受到JPEG有損壓縮的圖像，比較本文算法與文獻(xiàn)［4］算法嵌入秘密信息后能反映其載密圖像失真度的PSNR值,，如表1所示,。

4結(jié)論

　　本文提出了SVD和EMD-S結(jié)合的隱藏編碼算法，充分利用了奇異值分解的穩(wěn)定性,，將秘密信息通過S盒的壓縮變換嵌入到每個子塊的最大奇異值當(dāng)中,，矩陣編碼方便直接，信息隱藏量可觀,，既保證了載密圖像的質(zhì)量，也提高了算法的魯棒性。相關(guān)實(shí)驗(yàn)數(shù)據(jù)表明,，本文算法能夠較好地抵抗JPEG壓縮,，在相同嵌入容量下具有更好的PSNR值。因?yàn)楸疚奶岢龅乃惴ㄊ褂昧薙盒,，每個S盒占據(jù)了64個連續(xù)的存儲單元,，所以算法的空間復(fù)雜度變大了，也就是說,，犧牲了空間換取了時間,，在以后的算法研究中應(yīng)進(jìn)一步降低空間復(fù)雜度。

　　參考文獻(xiàn)

　?。?］ 韓佳伶.基于隱藏容量的數(shù)字圖像信息隱藏算法研究［D］.長春:吉林大學(xué),2015.

　?。?］ 劉粉林,劉九芬,羅向陽.數(shù)字圖像隱寫分析［M］.北京:機(jī)械工業(yè)出版社,2010.

　　［3］ Yao Xiaoming, Du Wencai, Wu Weihua. A robust EMD likestenographic schem［C］.Third International Symposium on Intelligent Information Technology and Security Informatics,2010:134 137.

　?。?］ 姚楚茂,湯光明,辜剛林.基于奇異值的魯棒性圖像隱寫算法［J］.計(jì)算機(jī)工程與設(shè)計(jì),2015,36(7):1727 1732.

　?。?］ 姚楚茂,湯光明,蔡鎮(zhèn).最大奇異值移位的魯棒性圖像信息隱藏［J］.計(jì)算機(jī)應(yīng)用研究,2015,32（7）：2172 2174.

　　［6］ 劉圓,潘峰.基于矩陣運(yùn)算的二維EMD算法［J］.計(jì)算機(jī)工程,2011,37(20):111 113.