吳文琪1，胡芳仁1,，2,，楊宇鑫1
（1.南京郵電大學(xué) 光電工程學(xué)院,，江蘇 南京 210046,；2.南京郵電大學(xué)Peter Gruenberg中心，江蘇 南京 210023）
摘要：基于聲表面波（SAW）理論以及SAW諧振器的結(jié)構(gòu)和工作原理,，設(shè)計(jì)了一種基于聲表面波（SAW）諧振式壓力傳感器,。采用有限元軟件COMSOL Multiphysics對(duì)ZnO單晶聲表面波諧振器進(jìn)行建模和仿真，提出符合聲表面波振型的對(duì)稱模態(tài)和反對(duì)稱模態(tài),，計(jì)算出ZnO單晶的相速度為3 237.31 m/s,。討論了ZnO基底厚度對(duì)此壓力傳感器的相速度的影響，得出ZnO基底厚度越大,，相速度越小,。最后通過(guò)加載0~1 000 kg/m2的質(zhì)量塊來(lái)模擬不同的壓力對(duì)器件的頻率響應(yīng)的影響，結(jié)果顯示壓力的變化與諧振頻率二者具有良好的負(fù)相關(guān)線性關(guān)系,。通過(guò)擬合得出線性表達(dá)式,。
關(guān)鍵詞：聲表面波；ZnO單晶,；壓力傳感器
中圖分類號(hào)：TP391.9,；TP211+.51文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674-7720.2016.24.024
引用格式：吳文琪，胡芳仁，楊宇鑫. 基于ZnO單晶聲表面波壓力傳感器的特性研究［J］.微型機(jī)與應(yīng)用,，2016,35（24）：84-86.
0引言
聲表面波(Surface Acoustic Wave,SAW)壓力傳感器所特有的高頻特性及器件基片材料的壓電,、逆壓電效應(yīng),使其與傳統(tǒng)壓力傳感器相比，具有測(cè)量精度高,、抗干擾性強(qiáng),、微型、無(wú)源無(wú)線及成本低等優(yōu)點(diǎn),，適用于易燃,、易爆、密閉等特定環(huán)境下的遙測(cè)與傳感［1］,。因此對(duì)于SAW壓力傳感器的研究具有重要的意義,。
在SAW器件應(yīng)用方面，由于ZnO的光電耦合系數(shù)高,，溫度系數(shù)低且廉價(jià)易得等特點(diǎn)［2］,，非常適合于制造高頻聲表面波器件。
為研究這一類器件,，本文依據(jù)壓電晶體的運(yùn)動(dòng)方程和壓電本構(gòu)方程［3］,，建立ZnO/Al結(jié)構(gòu)SAW 2D模型，采用物理耦合場(chǎng)軟件COMSOL Multiphysics對(duì)SAW諧振器器件進(jìn)行了仿真［4］,，確定了一種靈敏度較大的傳感器,，為實(shí)現(xiàn)SAW壓力傳感器的制造提供了理論基礎(chǔ)以及數(shù)據(jù)參考。
1工作原理
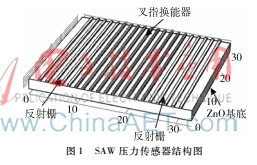
SAW傳感器的組成元件是叉指換能器（IDT）和聲反射柵［5］,，結(jié)構(gòu)如圖1所示,。其工作原理是：受空間電磁波的激勵(lì)后，在SAW諧振器基片表面激發(fā)與電磁波同頻的SAW,，SAW在兩個(gè)反射柵之間來(lái)回多次反射,。當(dāng)SAW諧振器基片受到壓力作用時(shí)，SAW諧振器尺寸發(fā)生變化,，假設(shè)應(yīng)變?yōu)棣?，此時(shí)的諧振頻率由（1）式算出。d是IDT兩相鄰電極中心距,，可見(jiàn)壓力的變化會(huì)引起諧振頻率的變化,，通過(guò)檢測(cè)fr的變化實(shí)現(xiàn)對(duì)外力的監(jiān)測(cè)。
當(dāng)有壓力加載在聲表面波傳播表面時(shí),，主要考慮有效彈性系數(shù)的變化量為：c*ijkl=cijkl+cijkl＾,，壓電介質(zhì)的耦合波方程變?yōu)椋?/p>
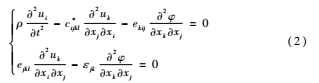
式（2）為有負(fù)載時(shí)壓電介質(zhì)的耦合波方程。其中,，φ為電勢(shì),，ρ為介質(zhì)的密度, xj為介質(zhì)中的位置坐標(biāo), ui為彈性介質(zhì)的位移, cijkl為二階彈性剛度常數(shù)，ekij為壓電常數(shù)，εjk為介電常數(shù),。
2仿真與結(jié)果分析
本文采用有限元軟件COMSOL,，結(jié)合壓電晶體的運(yùn)動(dòng)方程和壓電本構(gòu)方程，對(duì)ZnO單晶聲表面波諧振器進(jìn)行建模和仿真,，對(duì)其特征頻率進(jìn)行仿真分析,，并分析壓力加載下器件的頻率響應(yīng)，以探討壓力的變化與諧振頻率的關(guān)系,，對(duì)使用SAW諧振器實(shí)現(xiàn)對(duì)壓力的測(cè)量提供了支持。
2.1二維結(jié)構(gòu)模型建立
首先,，建立單端口諧振器的二維幾何模型（見(jiàn)圖2）,，叉指換能器和聲反射柵的材料為Al，基底材料為ZnO,。假設(shè)設(shè)計(jì)波長(zhǎng)為20 μm,，基片厚度為80 μm，寬度為215 μm,。IDT與反射柵的寬度為5 μm,，厚度為0.3 μm。IDT與反射柵的間隔為5 μm,。邊界條件如表1所示,。
2.2特征頻率研究
利用COMSOL對(duì)ZnO單晶聲表面波諧振器進(jìn)行多物理域耦合建模與仿真，得到兩個(gè)聲表面波模態(tài)（即對(duì)稱模態(tài)與反對(duì)稱模態(tài)）所對(duì)應(yīng)的諧振頻率（fsc+）與反諧振頻率（fsc-）,。圖3和圖4分別為對(duì)稱模態(tài)和反對(duì)稱模態(tài),，縱坐標(biāo)為總位移，圖中最右邊的標(biāo)尺表示總位移的大小,，從上往下逐漸減小,。
從圖3中可以看出對(duì)稱模態(tài)對(duì)應(yīng)的諧振頻率為1.618 511×108Hz，振動(dòng)最強(qiáng)的質(zhì)點(diǎn)總位移有1.04×10-3μm,。圖4為反對(duì)稱模態(tài)變形圖,，反對(duì)稱模態(tài)對(duì)應(yīng)的諧振頻率為1.618 799×108Hz,最強(qiáng)的質(zhì)點(diǎn)總位移有9.65×10-4 μm。ZnO單晶材料沿縱坐標(biāo)軸0~60 μm的區(qū)域內(nèi)各質(zhì)點(diǎn)的振動(dòng)位移幾乎為0,，聲表面波能量主要集中在1~2個(gè)波長(zhǎng)范圍,，符合聲表面波的特性。
由式（3）所示的聲表面波波速與正反模態(tài)諧振頻率的公式,，可計(jì)算出ZnO單晶的聲表面波的相速度νeff=3 237.31 m/s,。
νeff=d×(fsc++fsc-)（3）
其中，d是IDT兩相鄰電極中心距,，下面利用COMSOL的頻率分析模塊研究在諧振頻率附近不同頻率下的總位移,。圖5是總位移與頻率的關(guān)系圖，橫坐標(biāo)頻率為160~163 MHz，縱坐標(biāo)的單位是總位移,。由圖可知,，當(dāng)器件處于諧振狀態(tài)時(shí)，IDT激發(fā)出的聲表面波總位移最大,，叉指換能器所產(chǎn)生的聲波是最強(qiáng)的,，與叉指換能器的工作原理相符合。
2.3ZnO基底厚度對(duì)聲表面波波速的影響
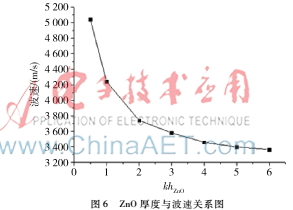
通過(guò)改變ZnO基底的厚度,，得到khZnO與聲表面波波速的關(guān)系,，其中，k=2π/λ為波速,。由圖6可見(jiàn),，當(dāng)khZnO從0增加到6時(shí)，聲表面波波速逐漸變小,。因此在設(shè)計(jì)ZnO單晶SAW諧振器時(shí),，可以通過(guò)調(diào)節(jié)基底厚度得到不同的聲表面波波速。
2.4壓力加載下的頻率響應(yīng)分析
在ZnO基底上依次加載0~1 000 kg/m2的質(zhì)量塊來(lái)模擬壓力的變化,。加載質(zhì)量塊后,，找到正反模態(tài)對(duì)應(yīng)的諧振頻率，由公式（4）可以得到諧振頻率,。不同壓力下的諧振頻率如表2所示,。
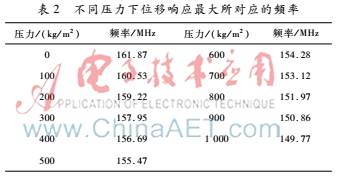
通過(guò)對(duì)表2數(shù)據(jù)的擬合，畫出諧振頻率的擬合線如圖7所示,，以得到諧振頻率與外加壓力之間呈負(fù)相關(guān)的線性關(guān)系,，即當(dāng)壓力增加時(shí),，頻率呈近似線性下降。通過(guò)擬合可以得出線性表達(dá)式：
y=161.87-0.0125x
3結(jié)論
本文根據(jù)諧振器的結(jié)構(gòu)和工作原理，結(jié)合壓電晶體的運(yùn)動(dòng)方程和壓電本構(gòu)方程,，利用有限元分析軟件COMSOL對(duì)ZnO單晶聲表面波諧振器進(jìn)行建模與仿真,，提出了符合聲表面波振型的對(duì)稱模態(tài)和反對(duì)稱模態(tài),。通過(guò)對(duì)壓力加載下的頻率響應(yīng)進(jìn)行分析,，得到壓力與SAW諧振器頻率成負(fù)相關(guān)的線性關(guān)系，這對(duì)使用SAW諧振器實(shí)現(xiàn)對(duì)壓力的測(cè)量提供了支持,。
參考文獻(xiàn)
?。?］ BENSMAINE S, BENYOUCEF B. Experimental characterization of ZnO thins films and identification of frequency peaks in ZnO/SiO2/Si SAW devices［J］. American Journal of Materials Science, 2013, 3(4):100 103.
［2］ 周劍, 何興理, 金浩,等. 基于ZnO壓電薄膜的柔性聲表面波器件［J］. 光學(xué)精密工程, 2014, 22(2):346 350.
?。?］ Zhao Yiyu, Li Honglang, He Shitang. Optimal cut of quartz for a surface acoustic wave pressure sensor with nonuniform pressure load［C］. 2013 Symposium on Piezoelectrioity, Acoustic waues and Device Applications (SPAWDA), 2013:1 3.
?。?］ NAMDEO A K, NEMADE H B. FEM study on the effect of metallic interdigital transducers on surface acoustic wave (SAW) Velocity in SAW Devices［D］. Guwahati, India: Indian Institute of Technology, 2009.
［5］ 潘峰. 聲表面波材料與器件［M］. 北京：科學(xué)出版社, 2012.