凡旭國1,2,，周金治1,2，高磊1,，2

　?。?．西南科技大學(xué) 信息工程學(xué)院，四川 綿陽 621010; 2．特殊環(huán)境機(jī)器人技術(shù) 四川省重點(diǎn)實(shí)驗(yàn),，四川 綿陽 621010）

        摘要：鋰離子電池管理系統(tǒng)設(shè)計(jì)及荷電狀態(tài)（SOC）估算依賴于電池等效電路模型的建立,，在幾種常見的動力鋰離子電池等效電路模型分析與比較的基礎(chǔ)上,，通過對動力鋰離子電池進(jìn)行多種特性實(shí)驗(yàn)，分析了鋰離子電池的動態(tài)特性,，提出了二階RC等效電路模型,，并驗(yàn)證了模型的準(zhǔn)確性。在電路模型基礎(chǔ)上運(yùn)用擴(kuò)展卡爾曼濾波算法搭建了MATLAB/Siumlink平臺上的仿真模型,，通過仿真和實(shí)驗(yàn)結(jié)果的對比,，驗(yàn)證該模型具有較高的估算精度，可用于鋰離子電池SOC的實(shí)時(shí)估算,。

　　關(guān)鍵詞：鋰離子電池;等效電路模型; EKF算法; SOC估算

　　中圖分類號：TM912.9文獻(xiàn)標(biāo)識碼：ADOI： 10.19358/j.issn.1674-7720.2017.02.025

　　引用格式：凡旭國,，周金治,，高磊.鋰離子電池特性建模與SOC估算算法的研究［J］.微型機(jī)與應(yīng)用,，2017,36（2）：83-86.

0引言

　　*基金項(xiàng)目：特殊環(huán)境機(jī)器人技術(shù)四川省重點(diǎn)實(shí)驗(yàn)室基金資助項(xiàng)目（13ZXTK07）;西南科技大學(xué)研究生創(chuàng)新基金資助項(xiàng)目（16ycx100）可充放電鋰離子電池自從20世紀(jì)90年代出現(xiàn)以來，由于具有體積小,、質(zhì)量輕,、無記憶效應(yīng)、無污染,、可快速充放電等優(yōu)勢,，已廣泛應(yīng)用于手機(jī)、筆記本電腦,、數(shù)碼相機(jī)等便攜式電子產(chǎn)品［1］,。電池使用時(shí)其荷電狀態(tài)（SOC）的估算是電池管理系統(tǒng)（BSM）中的重要環(huán)節(jié)，準(zhǔn)確地估算SOC能夠提高電池的安全性能,，有效地保護(hù)電池,，延長電池的循環(huán)使用壽命，提高電池的使用效率［2］,。

　　SOC估算算法的精確性直接依賴于用來描述電池特性的電路模型的準(zhǔn)確性,。常用的電池模型主要有三類［3］：電化學(xué)機(jī)理模型、神經(jīng)網(wǎng)絡(luò)模型和等效電路模型,。由于電池內(nèi)部化學(xué)反應(yīng)復(fù)雜,，很難在實(shí)際應(yīng)用中建立精確的電化學(xué)機(jī)理模型；而神經(jīng)網(wǎng)絡(luò)模型則需要大量的歷史數(shù)據(jù)來預(yù)測電池性能,，并且模型只能針對特定因素分析,，難以全面反映電池特性；等效電路模型能夠考慮電壓,、電流,、溫度、極化等多種因素的影響,，使用基本電路元件組成電路描述電池的工作特性,，物理意義清晰明確,，因而得到廣泛應(yīng)用。

　　目前國內(nèi)外常用的等效電路模型包括：Rint模型,、Thevenin模型,、PNGV模型以及文獻(xiàn)［4］提出的對PNGV模型改進(jìn)的GNL模型等。文獻(xiàn)［5］運(yùn)用插值估算法結(jié)合PNGV模型對SOC進(jìn)行了估算,，有效地解決了安時(shí)法存在累計(jì)誤差和初始值不準(zhǔn)確的問題,，最終使誤差控制在5%以內(nèi)；文獻(xiàn)［6］將EKF算法用在一階RC電路模型上,，雖然取得一定的效果,，但是考慮影響電池SOC的因素不夠全面；文獻(xiàn)［7］用神經(jīng)網(wǎng)絡(luò)和EKF相結(jié)合的方法實(shí)現(xiàn)了SOC的在線估計(jì),，但是依賴于電池大量的離線數(shù)據(jù)訓(xùn)練,；文獻(xiàn)［8］在等效電路模型的基礎(chǔ)上將自適應(yīng)滑模觀測器運(yùn)用于SOC的估算中，最后建立了仿真模型驗(yàn)證了方法的可行性,，但算法誤差和有效性不能得到保證,。

　　本文通過對動力18650型鋰離子電池進(jìn)行多次充放電實(shí)驗(yàn)，分析了鋰離子電池的動態(tài)特性,，提出了二階RC等效電路模型,，并辨識了模型的相關(guān)參數(shù)，最后在MATLAB/Siumlink仿真平臺上建立仿真模型,，對模型進(jìn)行仿真驗(yàn)證,，通過仿真和實(shí)驗(yàn)結(jié)果的對比，驗(yàn)證該模型具有較高的估算精度,。

1鋰離子電池特性實(shí)驗(yàn)

　　1.1充電實(shí)驗(yàn)

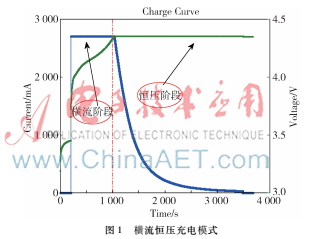
　　鋰離子電池常采用恒流轉(zhuǎn)恒壓的充電模式,，本文以額定容量為2 600 mAh、充電電壓4.3 V,、標(biāo)稱充電電流0.25C~1C的18650型鋰離子電池,，實(shí)驗(yàn)平臺為美諾M9710可編程電子負(fù)載和數(shù)控電源，通過實(shí)驗(yàn)可以獲取其充電過程中電壓電流的變化曲線,，如圖1所示,。

　　1.2放電實(shí)驗(yàn)

　　鋰離子電池在不同的放電倍率下端電壓響應(yīng)不同，為獲得電池在工作過程中端電壓的變化,，分別以0.3C,、0.5C、1C放電倍率對電池進(jìn)行恒流放電實(shí)驗(yàn),，得到各種倍率下電池的電壓隨時(shí)間變化的曲線如圖2所示,。

　　1.3復(fù)合脈沖實(shí)驗(yàn)

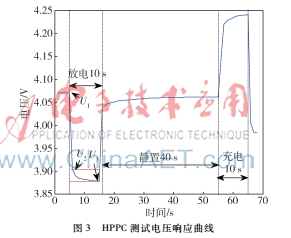
　　復(fù)合脈沖測試（Hybrid Pulse Power Characterization,HPPC）的目的是測試電池的動態(tài)特性，同時(shí)也可用來識別模型參數(shù),。首先進(jìn)行10 s放電脈沖,，經(jīng)過40 s靜置后再進(jìn)行10 s充電脈沖,，整個(gè)過程采用1C（即2.6 A）恒定電流充放電，并在HPPC循環(huán)測試中讓電池等間隔SOC點(diǎn)進(jìn)行復(fù)合脈沖實(shí)驗(yàn),，選取SOC為0.1,，0.2,…,0.9，相鄰脈沖實(shí)驗(yàn)之間的間隔為1 h（注：對于2 600 mAh電池容量,，1C電流放電6 min,，即放出260 mAh,SOC值下降0.1），電池靜置1 h之后進(jìn)入下一個(gè)HPPC循環(huán),。SOC為0.5時(shí)HPPC測試對應(yīng)的電壓響應(yīng)曲線如圖3所示,。　

　　1.4OCV和SOC關(guān)系標(biāo)定實(shí)驗(yàn)

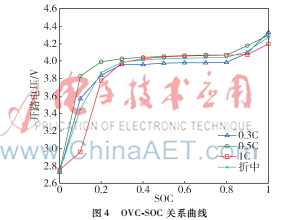
　　開路電壓（OCV）表征了電池在某一荷電狀態(tài)下所對應(yīng)的電動勢,，OCV與SOC具有一定的函數(shù)關(guān)系［9］,，實(shí)驗(yàn)分別采取0.3C、0.5C和1C的倍率放電,，每放出0.1SOC時(shí)靜置30 min,，將記錄到的電壓值作為對應(yīng)的開路電壓,，最終OCV和SOC的函數(shù)關(guān)系式通過對圖4中三者的折中曲線進(jìn)行多項(xiàng)式擬合得到,。　

　　2等效電路模型及驗(yàn)證

　　由電池的特性試驗(yàn)可以得知無論是施加充電電流還是放電電流,，其端電壓都存在一個(gè)突變,，之后又有一個(gè)緩慢變化的過程，因此可以用一個(gè)歐姆內(nèi)阻和兩個(gè)表征電池內(nèi)部極化效應(yīng)的RC環(huán)節(jié)來模擬電池的特性,。等效電路模型如圖5所示,。

　　電池工作過程中模型的參數(shù)是動態(tài)變化的，因此模型中的五個(gè)參數(shù)需要進(jìn)行參數(shù)的辨識,。其中R0用電壓突變階段即式(1)得到,，兩個(gè)RC環(huán)節(jié)的參數(shù)用型如式(2)的二階指數(shù)在MATLAB的cftool工具箱中采用擬合方式得到，

　　R0=U1-U2I (1)

　　f(x)=a*exp(-τ1*x)+c*exp(-τ2*x)(2)

　　式中τ1=RsCs,、τ2=RlCl,。

　　得到模型參數(shù)之后，在MATLAB/Simulink平臺上建立二階RC等效電路模型,，設(shè)置仿真參數(shù)與自定義工況的實(shí)驗(yàn)數(shù)據(jù)做對比,。圖6為間歇橫流放電下仿真電壓與真實(shí)電壓的對比，由圖可見仿真值與真實(shí)值吻合較好,，同時(shí)也驗(yàn)證了所建模型的準(zhǔn)確性,。

　3EKF算法流程及實(shí)現(xiàn)

　　由于標(biāo)準(zhǔn)卡爾曼濾波算法只能用于線性系統(tǒng)，而擴(kuò)展卡爾曼濾波算法（EKF）是通過將非線性系統(tǒng)的狀態(tài)空間方程進(jìn)行線性化處理,，再利用卡爾曼濾波算法的遞推過程對系統(tǒng)狀態(tài)進(jìn)行最優(yōu)估算,，因此本文采用EKF結(jié)合二階RC模型的方法進(jìn)行SOC的估算,。

　　3.1EKF算法流程

　　EKF算法的非線性離散狀態(tài)空間方程為［10］：

　　xk+1=f(xk,uk)+wk

　　yk=g(xk,uk)+vk（3）

　　式中，f(xk,uk)是非線性狀態(tài)轉(zhuǎn)移函數(shù),，g(xk,uk)是非線性測量函數(shù),。

　　首先，由基爾霍夫電壓和電流定理得圖5所示電路的時(shí)域方程如下：

　　i=CsdUsdt+UsRs

　　i=CldUldt+UlRl

　　Ubat=Uoc(SOC)-Us(t)-Ul(t)-R0i（4）

　　系統(tǒng)的狀態(tài)量需要SOC,，根據(jù)式（5）安時(shí)積分法的定義:

　　SOCt=SOC0-η∫t0idtQ（5）

　　選取SOC和兩電容上的電壓為狀態(tài)量,，對式(4)和式(5)進(jìn)行離散化處理得到系統(tǒng)的更新方程如式（6）所示，測量方程如式（7）所示,。

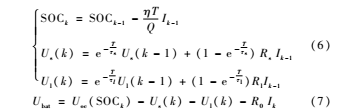
　　其次,，令狀態(tài)變量xk=［SOCkUs(k)Ul(k)］T,將式（6）、式（7）轉(zhuǎn)化為矩陣形式：

　　最后,，采用EKF算法的遞推過程實(shí)現(xiàn)SOC的實(shí)時(shí)估算,，具體步驟如下：

　　(1)初始化x0和P0。

　　(2)根據(jù)初值得到k時(shí)刻的狀態(tài)向量的預(yù)測估計(jì)和均方誤差的預(yù)測估計(jì):

　　(3)計(jì)算卡爾曼濾波增益:

　　(4)根據(jù)k時(shí)刻測量值和卡爾曼濾波增益Gk修正狀態(tài)向量估計(jì)值,，得到狀態(tài)向量及均方誤差的最優(yōu)估計(jì):

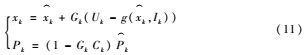
　　(5)返回步驟（2）進(jìn)行下一輪估算,，如此循環(huán)迭代就能得出每個(gè)時(shí)刻的SOC值。

　　3.2算法的實(shí)現(xiàn)

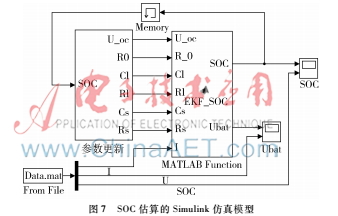
　　基于以上算法的分析,，在MATLAB/Simulink平臺上建立如圖7所示的SOC估算仿真框圖,。該模型的輸入為實(shí)際的電流，當(dāng)前時(shí)刻的SOC估計(jì)值作為上一時(shí)刻的輸入形成閉環(huán)系統(tǒng),，經(jīng)過算法模塊的迭代更新可在線得到每一時(shí)刻SOC的最優(yōu)估計(jì),，將仿真結(jié)果與真實(shí)SOC比較來驗(yàn)證算法的魯棒性。

　　3.3算法的仿真驗(yàn)證

　　將實(shí)際實(shí)驗(yàn)測試的.mat數(shù)據(jù)輸入模型中,，設(shè)置好仿真時(shí)間,，采樣間隔取1 s，經(jīng)過模型的遞推估算可實(shí)時(shí)在線地得出每一時(shí)刻SOC的最優(yōu)估計(jì),。

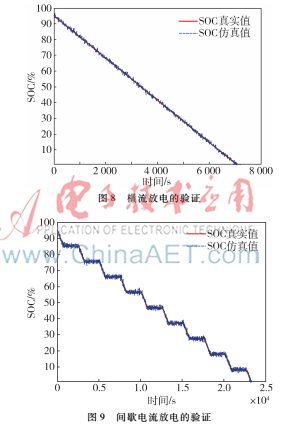
　　圖8和圖9分別顯示了0.5C橫流放電和間歇電流放電時(shí)真實(shí)的SOC和模型仿真出的SOC,，結(jié)果表明，該算法估算出來的SOC值和真實(shí)值吻合度較好,，并且無論是哪一種放電工況其誤差都不超過5%,。　

4結(jié)論

　　本文通過充放電,、HPPC實(shí)驗(yàn)以及開路電壓實(shí)驗(yàn)建立了二階RC等效電路模型來模擬電池的動態(tài)特性,，并對模型進(jìn)行了驗(yàn)證，針對鋰離子電池工作過程中的非線性,，提出了基于等效電路模型的擴(kuò)展卡爾曼濾波算法并對算法的流程進(jìn)行了分析,，最后在MATLAB/Simulink平臺上搭建了SOC估算的模型，驗(yàn)證了無論是橫流還是間歇電流工況下該算法的誤差都能控制在5%以內(nèi),。

參考文獻(xiàn)

　?。?］ BESTER J E, EL H A, MABWE A M. Modelling of lithiumion battery and SOC estimation using simple and extended discrete Kalman Filters for Aircraft energy management［C］.Industrial Electronics Society, IECON 201541st Annual Conference of the IEEE. IEEE, 2015: 2433-2438.

　?。?］ ALVAREZ A J C, GARCIA N P J, de COS J F J, et al. Battery stateofcharge estimator using the MARS technique［J］. IEEE Transactions on Power Electronics, 2013,28(8):3798-3805.

　　［3］ He Hongwen, Xiong Rui, Fan Jinxin. Evaluation of lithiumion battery equivalent circuit models for state of charge estimation by an experimental approach［J］. Energies, 2011,4(12):582-598.

　?。?］ 林成濤,仇斌,陳全世.電流輸入電動汽車電池等效電路模型的比較［J］.機(jī)械工程學(xué)報(bào),2005,41(12):7681.

　?。?］ 楊陽,湯桃峰,秦大同,等.電動汽車鋰電池PNGV等效電路模型與SOC估算方法［J］.系統(tǒng)仿真學(xué)報(bào), 2012,24(4):938-942.

　　［6］ He Hongwen, Xiong Rui, Zhang Xiaowei, et al. Stateofcharge estimation of the lithiumion battery using an adaptive extended Kalman filter based on an improved Thevenin model［J］. IEEE Transactions on Vehicular Technology, 2011, 60(4): 1461-1469.

　?。?］ CHARKHGARD M, FARROKHI M. Stateofcharge estimation for lithiumion batteries using neural networks and EKF［J］. IEEE Transactions on Industrial Electronics, 2010,57(12):4178-4187.

　?。?］ Yin Chun, Zhong Qishui, Chen Yangquan, et al. Estimating the state of charge of lithium batteries based on fractionalorder slidingmode observer［C］.Fractional Differentiation and Its Applications (ICFDA), IEEE, 2014: 1-6.

　　［9］ WINDARKO N A, CHOI J. SOC estimation based on OCV for NiMH batteries using an improved takacs model［J］. Journal of Power Electronics, 2010,10(2):181-186.

　?。?0］ Yuan Shifei, Wu Hongjie, Yin Chengliang. State of charge estimation using the extended kalman filter for battery management systems based on the ARX battery model［J］. Energies, 2013,6(1):444-470.