史振華

　　(紹興職業(yè)技術(shù)學(xué)院,浙江 紹興 312000)

        摘要：針對云計算中無法合理分配資源的問題,提出了采用改進的粒子群算法對其進行分配,。由于粒子群算法存在局部收斂速度快,容易陷入局部最優(yōu)解的情況,從粒子的選擇,、參數(shù)調(diào)整和預(yù)防過早收斂三個方面進行改進: (1)選擇粒子的時候采用適應(yīng)值最小的粒子,并根據(jù)約束函數(shù)淘汰不合格的粒子;(2)對慣性因子、個體最優(yōu)因子和全局最優(yōu)因子進行改進;(3)通過設(shè)定系數(shù)來防止算法過早收斂,。仿真說明,將改進后的算法運用在云計算方面,在云計算的資源失效,、云端用戶完成時間和云計算環(huán)境下的能量消耗三個方面都優(yōu)于粒子群算法。

　　關(guān)鍵詞：粒子群算法;云計算;資源分配

　　中圖分類號：TP393文獻標識碼：ADOI： 10.19358/j.issn.1674-7720.2017.06.019

　　引用格式：史振華. 一種改進的粒子群算法在云計算資源中的研究［J］.微型機與應(yīng)用,，2017,36（6）：62-65.

0引言

　　云計算技術(shù)不斷發(fā)展,現(xiàn)在已經(jīng)成為了計算機界研究的一個熱點,。相應(yīng)地，云計算服務(wù)不斷發(fā)展壯大,其應(yīng)用領(lǐng)域越來越廣泛,。云計算是通過互聯(lián)網(wǎng)技術(shù)將海量的IT資源通過有償?shù)姆绞教峁┙o云端用戶,云計算服務(wù)商通過云計算數(shù)據(jù)中心對云環(huán)境中的資源進行統(tǒng)一的管理和分配,最大限度地保證云端負載均衡［1］,。由于云計算中的資源是動態(tài)的,而云端用戶的需求是實時性和多樣性的,因此采用固定資源分配的方式無法滿足云端用戶的需求,云計算服務(wù)商提供的服務(wù)以資源調(diào)度方案最優(yōu),整體利益最大化為主要目標。云計算資源調(diào)度是一個多任務(wù)的NP問題,不同的學(xué)者從不同的角度進行了研究,。文獻［2］提出了采用蛙跳結(jié)合神經(jīng)網(wǎng)絡(luò)的算法來解決云計算資源分配問題,；文獻［3］提出將改進的蟻群算法運用到云計算資源調(diào)度中,取得了比較好的效果；文獻［4］提出了采用改進的布谷鳥算法來進行資源分配,提高了資源的分配效率;文獻［5］提出將多維模型與蟻群算法進行相結(jié)合來進行云計算資源的分配,取得了比較好的效果,；文獻［6］提出了生物中的膜計算與蝙蝠算法相結(jié)合來解決云計算中的資源分配,；文獻［7］提出了采用粒子群算法與神經(jīng)網(wǎng)絡(luò)相結(jié)合的方法分配云計算資源,取得了比較好的效果。

　　本文將粒子群算法運用到云計算中進行資源分配,對于粒子算法存在的問題,分別從粒子的選擇,、參數(shù)調(diào)整和預(yù)防過早收斂三個方面進行改進,。仿真實驗說明本文算法相比于基本粒子群算法在資源分配方面有了明顯的改進。

1云計算資源簡述

　　云計算中的資源調(diào)度關(guān)系到云計算的運行效率,、能量消耗和時間花費等問題,。云計算中的每一個云用戶是云環(huán)境中的一個節(jié)點,每一個節(jié)點既使用服務(wù)又提供服務(wù),云用戶之間相互協(xié)作實現(xiàn)資源優(yōu)化配置。因此資源調(diào)度算法就成為資源配置的關(guān)鍵,如何設(shè)計一個良好的云計算資源算法是十分必要的,。云計算資源的調(diào)度過程如圖1所示,。

　　在云計算資源調(diào)度中,無論采用什么樣的資源調(diào)度策略,其目的都是為了更好地使用云計算資源為云用戶提供高質(zhì)量的服務(wù)。高效的云計算資源調(diào)度目標是在調(diào)度資源的時候保證云計算的服務(wù)質(zhì)量(包括服務(wù)的時間,、效率和可靠性),全面提高資源的利用率和負載均衡,實現(xiàn)利益的最大化,。

　　目前,用于云計算資源調(diào)度的是啟發(fā)式的算法,這些算法包括粒子群算法、遺傳算法,、蟻群算法和人工神經(jīng)網(wǎng)絡(luò)算法等,這些算法都具有良好的尋求最優(yōu)解的性能優(yōu)點,但容易因自身的原因陷入局部而造成算法收斂,。

　2改進的粒子算法在云計算中的應(yīng)用

　　2.1基本的粒子群算法

　　粒子群算法是通過個體之間的相互協(xié)作和相互影響不斷地通過迭代來獲得最優(yōu)解的,群體之間的信息共享協(xié)助群體進化。設(shè)定粒子群算法的目標搜索空間是N維的,粒子群由m個粒子構(gòu)成,粒子的位置就是一個解,設(shè)Vmax為粒子的最大速度,因此群體中的粒子位置和速度采用N維向量來表示,。其中,第k個粒子的位置為: Xk=(xk1,xk2,…,，xkn),，k∈［1,m］,第k個粒子的速度為Vk=(vk1,vk2,…，vkn),，k∈［1,m］,粒子在迭代過程中的最佳位置就是個體最優(yōu)解的位置:Pkbest=(Pk1,Pk2,…,，PkN),k=1,2,3,…，m,全局最優(yōu)解為:Gkbest=(Pg1,Pg2,，…,PgN),。當找到最優(yōu)解之后,通過目標函數(shù)求出粒子的適應(yīng)值,通過適應(yīng)度的大小衡量粒子的位置,然后繼續(xù)以個體最優(yōu)解和全局信息解來更新自身的位置改變粒子的運動速度,逐步獲得最優(yōu)解。因此,粒子的更新速度和位置如下:

　　Vki=ηVki+αλ(Pkn－Vkn)+βμ(Pgn－Xgn)(1)

　　Xkn=Xkn+Vkn(2)

　　式中,η為慣性參數(shù),α和β分別是學(xué)習因子,α是調(diào)節(jié)粒子向個體最優(yōu)位置靠近飛行,β是粒子向群體最優(yōu)位置飛行,通常情況下,慣性系數(shù)η取值為1,λ和μ為相互獨立的隨機數(shù),Vmax為設(shè)置的最大速度,。從以上分析可以發(fā)現(xiàn)粒子群算法中的最優(yōu)解是通過粒子之間的協(xié)作和相互競爭來獲得的,粒子在空間以一定的速度飛行,每個粒子的運動通過個體與群體來不斷地調(diào)整速度和運動方向,從而獲得最優(yōu)解,。

　　2.2粒子群算法的改進

　　在粒子群算法中,沒有辦法對粒子進行選擇,如果出現(xiàn)一些劣質(zhì)的粒子則會降低算法的收斂速度,影響算法的整體性能。此外,粒子是按照一定的準則進行更新的,根據(jù)粒子群的適應(yīng)度值進行參數(shù)調(diào)整使得粒子向最優(yōu)解靠攏,但是在迭代過程中的參數(shù)調(diào)整對后期的算法影響比較大,有可能導(dǎo)致搜索精度降低,，所以參數(shù)的設(shè)置對于算法的改進具有一定的影響,。因此根據(jù)粒子群算法實現(xiàn)的流程,本文從幾個方面進行改進:(1)對優(yōu)良粒子進行選擇,淘汰差的粒子;(2)對慣性因子、學(xué)習因子和群體因子進行調(diào)整,；(3)通過早熟對算法進行判斷和處理,。

　　2.2.1選擇粒子

　　粒子在進行算法初始化后,都有一個適應(yīng)值,對于最大優(yōu)化問題認定適應(yīng)值大的表示該粒子為優(yōu),反之,對于最小優(yōu)化問題則選擇適應(yīng)度值最小的粒子為優(yōu)。云計算中的資源調(diào)度目標是以花費最少資源,花費最少使用時間為代價來滿足用戶的需求,，因此在選擇粒子的時候應(yīng)該考慮適應(yīng)值最小的粒子,。本文的適應(yīng)度函數(shù)為:

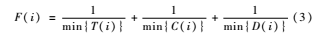
　　式中,T(i)表示第i個資源的時間消耗,C(i)表示第i個資源的成本消耗,D(i)表示第i個資源的帶寬消耗。

　　由于粒子算法在運行過程中必須對粒子的運動進行一定的約束,比如限定粒子的速度和運動的區(qū)域等條件,因此設(shè)定一個約束函數(shù)進行解決,約束函數(shù)如下:

　　Con(i)=∑hj=1max(0,gj(x))+∑rp=1|hp(x)|

　　s.tgj(x)≥0,j=1,2,…,，h

　　hp(x)=0,p=1,2,…,，r(4)

　　式中g(shù)j(x)是不等式的約束條件,hp(x)為等式約束條件,它反映了粒子距離的區(qū)域的程度,約束值越大的粒子應(yīng)該最先被淘汰。因此選擇粒子的策略如下:

　　(1)根據(jù)目標函數(shù)計算出粒子群中所有的粒子的初始值,并對其進行按照從大到小的順序進行排序,。

　　(2)由約束函數(shù)計算出粒子群中的粒子的約束值,。

　　(3)根據(jù)實際情況對粒子進行淘汰,根據(jù)式(3)和式(4)的結(jié)果對不合格的粒子進行淘汰,通過設(shè)定一定的比例和閾值對其粒子進行篩選。

　　2.2.2參數(shù)調(diào)整

　　前文已經(jīng)闡述了粒子群算法中的參數(shù)的影響對于粒子的性能是巨大的,由于慣性因子對于算法的優(yōu)化性能非常直接,當慣性因子的值小的時候,可以加速算法的收斂,當慣性因子的值大的時候,可以跳出局部最優(yōu)解,學(xué)習因子α影響著個體最優(yōu)的搜索效率,群體學(xué)習因子β影響著整個群體的最優(yōu)的搜索,因此,本文對這三個參數(shù)進行調(diào)整,。

　　(1)對于慣性因子的調(diào)整:

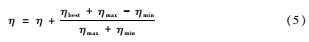
　　式中,ηmax和ηmin分別為慣性因子的最大值和最小值,ηbest為當前狀態(tài)中的最優(yōu)值,ηbest+ηmax－ηminηmax+ηmin為整體增量,。

　　(2)對于個體學(xué)習因子的調(diào)整：

　　α=α+φN(6)

　　式中,φ為群體增量系數(shù),N為種群規(guī)模，φN為個體學(xué)習因子增量,。

　　(3)對于群體學(xué)習因子的調(diào)整：

　　β=β+ψN(7)

　　式中,ψ為群體學(xué)習增量系數(shù),N為種群規(guī)模,ψN為群體學(xué)習因子,。

　　2.2.3算法過早收斂判斷

　　粒子群算法自身的結(jié)構(gòu)并不復(fù)雜,但算法在實現(xiàn)過程中容易出現(xiàn)粒子向著局部最優(yōu)位置靠近的情況,這樣很容易造成算法的局部過早收斂,過早得到局部最優(yōu)解從而耽誤了出現(xiàn)全局最優(yōu)解的可能,使得算法過早地陷入了早熟的情況。因此算法有必要對早熟進行判斷,。由于粒子群算法中的粒子的位置決定著粒子適應(yīng)度,換而言之,，粒子的適應(yīng)度反映了粒子的位置關(guān)系,因此可以將粒子的適應(yīng)度作為是否早熟的條件來進行判斷。假設(shè)粒子群算法的數(shù)目為k,F(i)avg表示粒子群的平均適應(yīng)度值,Ω表示粒子的聚集度：

　　其中Ω表示粒子群算法聚合離散的程度,Ω的值越大說明聚集度越低,反之,說明聚集度越高,。因此Ω數(shù)值越小越好,當Ω值越來越大的時候,粒子群中的粒子越來越分散,當大到一定程度的時候,算法滿足了終止條件,就陷入了收斂,因此設(shè)定一個常數(shù)Λ來避免這種情況的發(fā)生,當Ω>Λ的時候,就需要進行處理,。由于慣性權(quán)重比較小的時候是有利于算法收斂的,但式(5)的值不斷變大調(diào)整,因此需要引入一個系數(shù)Γ來約束慣性權(quán)重不斷地增大。當Ω>Λ時,η=Γη,。

　　2.3建立云計算的數(shù)學(xué)模型

　　在云計算的資源調(diào)度過程中,需要從整個網(wǎng)絡(luò)的帶寬,、任務(wù)響應(yīng)的延遲,、執(zhí)行時間等方面來進行考慮,既需要讓云端的用戶請求服務(wù)與云服務(wù)中的資源匹配,又能夠合理高效地滿足云計算的資源。設(shè)定目標函數(shù)為:

　　式中,Time(i)表示運行任務(wù)i需要的時間,Delay(i)表示運行任務(wù)i需要的延遲,Bandwith(i)表示運行任務(wù)i的網(wǎng)絡(luò)帶寬,，x+y+z=1。

　　2.4粒子群算法與云計算對應(yīng)關(guān)系

　　將云計算中的云端資源與改進的粒子群中的粒子信息進行對應(yīng),云計算中的資源選擇的過程就是改進粒子群算法中的粒子淘汰的過程,公式(10)中約束條件對應(yīng)粒子算法中的選擇條件,資源調(diào)度中的最優(yōu)解即為改進粒子群算法中的最優(yōu)解,。

　　2.5算法步驟

　　算法步驟如下：

　?。?）以設(shè)計最優(yōu)的云計算中的資源調(diào)度為目標,設(shè)定云計算資源與粒子群中的粒子之間的對應(yīng)關(guān)系

　　（2）根據(jù)問題確定粒子群數(shù)目,設(shè)置慣性初始值,、最大值和最小值,、個體學(xué)習因子、群體群體學(xué)習因子,、最大迭代次數(shù),、常數(shù)Λ和系數(shù)Γ、粒子初始化位置和速度,；

　?。?）根據(jù)公式(3)選擇粒子的初始適應(yīng)值,淘汰表現(xiàn)不合格的因子；

　?。?）根據(jù)粒子群算法要求和公式(5)~(7)不斷更新粒子的個體最優(yōu)和群體最優(yōu),迭代次數(shù)加1,；

　　（5）根據(jù)公式(9)判斷算法是否會進行過早收斂,如果收斂則進行處理,否則轉(zhuǎn)步驟（4）,；

　?。?）判斷是否達到最大次數(shù),如果達到則轉(zhuǎn)步驟（9）；否則執(zhí)行下一步,；

　?。?）判斷是否收斂,如果收斂則執(zhí)行下一步,否則執(zhí)行步驟（4）；

　?。?）確定群體最優(yōu)對應(yīng)的粒子信息;

　?。?）根據(jù)粒子信息確定最優(yōu)資源解；

　?。?0）算法結(jié)束,。

3仿真實驗

　　3.1搭建實驗環(huán)境

　　本文實驗選擇在操作系統(tǒng)為Windows 7,CPU為Inter Core T 6400,內(nèi)存為2 GB,硬盤為160 GB的臺式機上運行。采用Cloudsim仿真平臺進行實驗,。

　　3.2實驗結(jié)果分析

　　為了進一步說明本文算法相比與改進前的粒子群算法的效率,將本文的算法與基本的粒子群算法從執(zhí)行云計算的資源失效,、云端用戶完成時間和云計算環(huán)境下的能量消耗三個方面來進行分析。

　　(1)資源失效

　　將云計算資源中的實際能力,、存儲能力和通信能力作為評價資源淘汰的重要方面,設(shè)置慣性因子為2,個體學(xué)習因子為1.2,群體學(xué)習因子為2.2,最大迭代次數(shù)為500次,常數(shù)Λ和系數(shù)Γ分別為1.5和1,，用戶任務(wù)為20,資源數(shù)目為10、30,、50,、70,、90,進行資源調(diào)度,選擇10次的淘汰資源的平均數(shù)作為任務(wù)效率的判別標準,結(jié)果如表1和圖2所示。

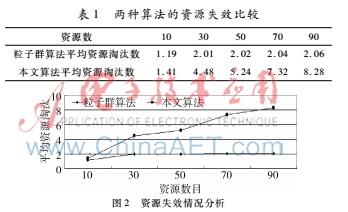
　　從表1和圖2中可以發(fā)現(xiàn),基本的粒子群算法的平均淘汰曲線基本上處于水平狀,并沒有明顯的向上發(fā)展的趨勢,而本文算法的平均資源淘汰曲線呈直線上升,這說明基本的粒子群算法沒有淘汰粒子,從而增加了算法在空間和時間上消耗,進一步延遲了算法最優(yōu)解的產(chǎn)生,。而本文算法通過淘汰狀態(tài)不佳的粒子,減少了算法規(guī)模,降低了迭代次數(shù),有利于云計算的資源調(diào)度,。

　　(2)云端用戶完成時間

　　設(shè)置虛擬任務(wù)為200個,使用本文算法與基本的粒子群算法進行比較,從圖3中的曲線來看,本文算法的幅度大于基本的粒子群算法,這說明本文算法通過對自身參數(shù)的改進,使得算法的效率更高,從而導(dǎo)致曲線的幅度在開始階段比較大,隨著虛擬任務(wù)數(shù)目不斷增多,算法趨于穩(wěn)定。從結(jié)果來看,本文算法的任務(wù)完成時間明顯優(yōu)于粒子群算法,。

　　(3)云用戶任務(wù)能量消耗

　　設(shè)置虛擬任務(wù)為200個,使用本文算法與基本的粒子群算法進行比較,從圖4中的曲線來看,本文算法在能量消耗方面明顯低于粒子群算法,這說明本文算法通過對自身過早收斂的改進提高了算法的性能,隨著虛擬任務(wù)數(shù)目不斷增多,曲線趨于穩(wěn)定,。這說明本文算法非常適合虛擬任務(wù)大的資源調(diào)度。

4結(jié)論

　　本文將粒子群算法運用在資源調(diào)度中,并針對傳統(tǒng)的粒子群算法存在的問題進行了改進,將改進后的算法運用在云計算的資源調(diào)度中,提高了資源分配效率,在仿真平臺中與粒子群算法進行比較,，取得了比較好的效果,。

參考文獻

　　［1］ 李喬.云計算研究現(xiàn)狀綜述［J］.計算機科學(xué),2011,38(4):32-36.

　?。?］ Chen Xuan.Research of improved shuffled frog leaping algorithm in cloud computing resources［J］.International Jouranl of Grid and Distributed Computing,2016,9(3):24-28.

　?。?］ 聶清彬,蔡婷,王寧. 改進的蟻群算法在云計算資源調(diào)度中的應(yīng)用［J］.計算機工程與設(shè)計,2016,37(8):2016-2020.

　　［4］ 葉華喬,丁善婷.基于改進的布谷鳥算法在云計算資源的研究［J］.計算機測量與控制,2014,22(12):4150-4154.

　?。?］ 蔣華,張樂乾,王鑫.基于多維評價模型及改進蟻群優(yōu)化算法的云計算資源調(diào)度策略［J］.計算機測量與控制,2015,23(7):2559-2562.

　?。?］ 寧彬,谷瓊,吳釗.基于膜計算的蝙蝠算法在云計算資源調(diào)度的研究［J］.計算機應(yīng)用研究,2015,32(3):830-83.

　　［7］ 趙宏偉,李圣普.基于粒子群算法和RBF神經(jīng)網(wǎng)絡(luò)的云計算資源調(diào)度方法研究［J］.計算機科學(xué),2016,43(3):113-116.