陳富琴,周淵平
(四川大學(xué) 電子信息學(xué)院 ,四川 成都610065)
摘要:波達(dá)方向(Direct of Arrival,DOA)估計(jì)技術(shù)漸漸成為移動(dòng)通信中的研究熱點(diǎn),當(dāng)用戶的信號(hào)方向未知時(shí),可以根據(jù)經(jīng)典算法多重信號(hào)分類(Multiple Signal Classification, MUSIC)和旋轉(zhuǎn)不變技術(shù)信號(hào)參數(shù)估計(jì)(Estimating Signal Parameters Viarotational Invariance Techniques,ESPRIT)等方法估計(jì)信號(hào)DOA。針對(duì)不同的信號(hào)采取不同的算法分析。對(duì)窄帶信號(hào),從信噪比、陣元數(shù)、快拍數(shù)等不同情況下對(duì)TLSESPRIT算法和MUSIC算法進(jìn)行了仿真實(shí)驗(yàn),并比較了TLSESPRIT算法與MUSIC算法的DOA性能。對(duì)寬帶信號(hào),主要重點(diǎn)分析了基于非相干信號(hào)處理算法(Incoherent Signalsubspace Method, ISM)的兩種改進(jìn)的方法,對(duì)低信噪比子帶賦予低權(quán)重或舍棄。通過仿真實(shí)驗(yàn),證明了改進(jìn)算法的優(yōu)越性,同時(shí)對(duì)兩種改進(jìn)算法的使用場(chǎng)合作了簡(jiǎn)單的分析。
關(guān)鍵詞:DOA;MUSIC算法;窄帶信號(hào);寬帶信號(hào)
中圖分類號(hào):TN911文獻(xiàn)標(biāo)識(shí)碼:ADOI: 10.19358/j.issn.1674-7720.2017.10.018
引用格式:陳富琴,周淵平.不同信號(hào)的DOA估計(jì)算法比較[J].微型機(jī)與應(yīng)用,2017,36(10):61-64,69.
0引言
近年來,用陣列信號(hào)處理技術(shù)實(shí)現(xiàn)對(duì)信號(hào)的波達(dá)方向(Direction of Arrival,DOA)估計(jì)成為了研究熱點(diǎn)。DOA估計(jì)是在空域、時(shí)域譜估計(jì)的基礎(chǔ)上發(fā)展來的一種技術(shù),是陣列信號(hào)處理中的一個(gè)重要研究方向。DOA估計(jì)就是確定同時(shí)處在空間某一區(qū)域內(nèi)多個(gè)感興趣的信號(hào)的空間位置( 即多個(gè)信號(hào)到達(dá)陣列參考陣元的方向角)。DOA估計(jì)技術(shù)在近二十多年來得到了廣泛的發(fā)展,并取得了大量的成果。
窄帶信號(hào)的MUSIC算法利用的是接收數(shù)據(jù)協(xié)方差陣的噪聲子空間的正交特性,而ESPRIT算法則是利用了數(shù)據(jù)協(xié)方差陣信號(hào)子空間的旋轉(zhuǎn)不變性[1]。本文著重分析了MUSIC和 TLSESPRIT算法,然后在不同條件下對(duì)這兩種算法的性能進(jìn)行了 MATLAB的仿真和分析。窄帶信號(hào)的頻率相對(duì)不變,故陣列流型依賴于信源方位角 ,因此從時(shí)域的快拍數(shù)即可進(jìn)行DOA估計(jì),而信源為寬帶信號(hào)時(shí),陣列流型矩陣依賴于頻率和角度,故需要在頻域構(gòu)建多個(gè)窄帶模型,進(jìn)而利用窄帶DOA估計(jì)的方法進(jìn)行處理。ISM算法是最早出現(xiàn)的寬帶DOA估計(jì)算法,該方法在高信噪比時(shí)簡(jiǎn)單有效,然而在低信噪比時(shí),由于某些頻段上的DOA估計(jì)效果非常差,導(dǎo)致整體性能較差,但是能量加權(quán)法(EWISM)和能量門限法(ETISM)兩種改進(jìn)算法有效地改善了ISM算法存在的不足[2]。
1MUSIC算法模型
對(duì)于遠(yuǎn)場(chǎng)信號(hào),波陣面考慮為平面波,在此假設(shè)信源為點(diǎn)源, 空間中有D個(gè)窄帶的遠(yuǎn)場(chǎng)信號(hào)輻射到以均勻線陣上,陣元個(gè)數(shù)為M,陣元間距為d,陣元接收信號(hào)為nm(t),m=1,2,…,M(噪聲互不相干且與信號(hào)不相干)。互不相關(guān)的信源信號(hào)為Sk(t),k=1,2,…,D。
信號(hào)可用如下的復(fù)包絡(luò)形式表示:
Xm(t)=∑Dk=1sk(t)e-j2π(m-1)dλsinθk+nm(t)(1)
寫成矩陣為形式為:
X(t)=AS(t)+N(t)(2)
求出接收矩陣的相關(guān)矩陣:
R=E{X(t)XH(t)}=APAH+σ2I(3)
其中,P=E{S(t)S(t)H},σ2為噪聲功率 。
對(duì)式(3)中的協(xié)方差矩陣R求其特征值和特征向量。
在理想的條件下,協(xié)方差矩陣R的最小特征值為噪聲方差σ2,且其重?cái)?shù)為MD,即有:
λD+1=…=λM=σ2(4)
根據(jù)式(9)可以知道信號(hào)源的數(shù)目(其中K為R最小特征值的重?cái)?shù)) :
D=M-K(5)
所以,M陣元可估計(jì)的最大信源數(shù)為:
Dmax=M-1(6)
矩陣的特征向量相互正交,因?yàn)樽钚√卣髦禐樵肼暤呢暙I(xiàn),所以其對(duì)應(yīng)的那些特征向量構(gòu)成噪聲子空間,剩余的特征向量構(gòu)成信號(hào)子空間,且信號(hào)子空間與噪聲子空間相互垂直。
在信號(hào)源所在的方向上,方向向量a(θk)⊥ΩN(θk),k=1,2,…,D,處于信號(hào)子空間ΩS中,所以有:a(θk)⊥ΩN,構(gòu)造矩陣:
En=[υD+1,…,υM](7)
則有:En⊥a(θk)=0,k=1,2,…,D
根據(jù)式(7)可以求得空間譜,搜索空間譜的最大值,即為入射方向。
2ESPRIT算法模型
以均勻線陣為研究背景,信號(hào)位于遠(yuǎn)場(chǎng),從而在均勻各向同性的介質(zhì)中到達(dá)陣列的是平面波。假設(shè)加性噪聲在所有天線單元上都存在,而且是平穩(wěn)零均值隨機(jī)過程。將陣列描述為由兩個(gè)子陣構(gòu)成,這兩個(gè)子陣在各方面都是相同的,只是彼此有一個(gè)已知的位移矢量的偏移。
ESPRIT算法的基本思想是:研究由陣列的位移不變特性而引起的信號(hào)子空間的旋轉(zhuǎn)不變性,信號(hào)子空間是由數(shù)據(jù)矩陣X和Y張成的,均張成了維數(shù)為K的信號(hào)子空間,即矩陣A的列向量張成的空間,但Y張成的信號(hào)子空間旋轉(zhuǎn)了一個(gè)相位[3]。
LSESPRIT 普通最小二乘的基本思想是用一個(gè)范數(shù)平方為最小擾動(dòng)去干擾信號(hào)子空間,其目的是校正信號(hào)子空間中存在的噪聲。
TLSESPRIT總體最小二乘的基本思想是同時(shí)擾動(dòng)信號(hào)子空間和噪聲子空間,并使擾動(dòng)范數(shù)的平方保持最小。
ESPRIT算法的流程圖如圖1所示。

3TLSESPRIT與MUSIC對(duì)比實(shí)驗(yàn)
實(shí)驗(yàn)中,對(duì)信號(hào)DOA估計(jì)采用方差來衡量性能,并認(rèn)為估計(jì)角度誤差在2°范圍內(nèi)都是正確的估計(jì)。
(1)不同SNR下兩種算法的對(duì)比
仿真條件:均勻線陣陣元數(shù)目M=8;一個(gè)信號(hào)源,快拍數(shù)N=100,入射角度DOA=10°,不同SNR下進(jìn)行100次蒙特卡洛仿真,準(zhǔn)確度及估計(jì)方差如圖2所示。

由圖2可知, 隨著SNR的增加,兩種算法DOA估計(jì)方差在減小,MUSIC算法DOA估計(jì)性能優(yōu)于TLSESPRIT算法,方差更小,正確率更高。
(2)不同快拍數(shù)N下兩種算法的比較
仿真條件:均勻線陣陣元數(shù)目M=8;一個(gè)信號(hào)源,SNR=0 dB,入射角度DOA=10°,不同快拍數(shù)下進(jìn)行100次蒙特卡洛仿真,仿真結(jié)果如圖3所示。

由圖3可以看出隨著快拍數(shù)的增加,兩種算法DOA估計(jì)的方差在減小,MUSIC算法DOA估計(jì)性能優(yōu)于TLSESPRIT算法,方差更小,正確率更高。
(3)不同入射角度下兩種算法的比較
仿真條件:均勻線陣陣元數(shù)目M=8;一個(gè)信號(hào)源,快拍數(shù)N=100,SNR=0 dB,不同入射角度下進(jìn)行100次蒙特卡洛仿真,如圖4所示。
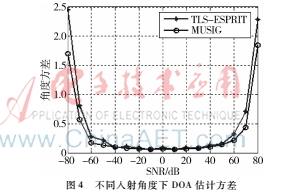
由圖4可知,入射角度在-60°~60°的角度范圍內(nèi)DOA估計(jì)方差小,角度越靠近90°,DOA估計(jì)性能越差。
(4)兩個(gè)信源時(shí)DOA估計(jì)結(jié)果直方圖
仿真條件:均勻線陣陣元數(shù)目M=8;一個(gè)信號(hào)源,快拍數(shù)N=100,SNR=0 dB,入射角度DOA=[10,20],進(jìn)行100次蒙特卡洛仿真,得到直方圖如圖5所示,DOA估計(jì)結(jié)果如表1所示。

由圖5可知, MUSIC算法具有更高的分辨力,方差更小,性能更優(yōu)。
4寬帶信號(hào)ISM算法
對(duì)于窄帶信號(hào),其頻率為常量,而寬帶信號(hào)包含了大量的頻點(diǎn),頻率是變量,當(dāng)信號(hào)變?yōu)閷拵盘?hào)時(shí),陣列的流型矩陣A會(huì)發(fā)生變化。
第m個(gè)陣元在采樣時(shí)刻t的輸出為:
Xm(t)=∑Di=1si(t-τmi)+nm(t)(8)
其中,τmi表示第m個(gè)陣元對(duì)第i個(gè)信號(hào)相對(duì)于參考陣元的延遲。
對(duì)式(8)通過DFT變換到頻域:
Xm(f)=∑Di=1Si(f)e-j2πfτmi+Nm(f)(9)
則陣列接收數(shù)據(jù)的頻域矩陣表示形式如下:
X(f)=A(f,θ)S(f)+N(f)(10)
其中X(f),S(f),N(f)分別是陣列接收數(shù)據(jù)、信號(hào)、噪聲經(jīng)DFT變換后的頻域數(shù)據(jù):
A(f,θ)=[a1(f,θ),a2(f,θ),…,aD(f,θ)]
ai(f,θ)=[e-j2πfτ1i,e-j2πfτ2i,…,e-j2πfτMi]T
(1)EW-ISM算法
寬帶信號(hào)在各個(gè)頻率成分上的能量分布不均,ISM算法對(duì)于信噪比較低的頻率點(diǎn),進(jìn)行估計(jì)的精度低,效果差,用以平均空間譜函數(shù)會(huì)使得估計(jì)誤差增大。采用改進(jìn)的EWISM算法對(duì)能量小的頻點(diǎn)賦予小的權(quán)重,對(duì)能量大的頻點(diǎn)賦予大的權(quán)重,最后對(duì)所有頻點(diǎn)進(jìn)行加權(quán)平均得到最終的空間譜[4]。
(2)ETISM算法
ISM算法由于在每個(gè)頻點(diǎn)都需要進(jìn)行DOA估計(jì),因此,算法的計(jì)算量很大,實(shí)時(shí)性不好。ETISM算法是先求出各個(gè)子帶上的能量值,然后設(shè)定一個(gè)合適的能力門限,若某一子帶的能量大于該門限,則對(duì)其進(jìn)行窄帶空間譜處理,反之,則不予考慮。例如,以所有子帶能量的均值為門限[5]。
4.1ISM算法DOA估計(jì)仿真實(shí)驗(yàn)
實(shí)驗(yàn)條件:兩個(gè)線性調(diào)頻信號(hào),頻率范圍分別為:0~100 Hz,100~200 Hz,SNR=[10,10],陣元數(shù)M=8,陣元間距為最高頻率對(duì)應(yīng)半波長(zhǎng),劃分子帶數(shù)目:J=64,頻域快拍K=32; DOA=[0,20],采用ISM算法,仿真結(jié)果如圖6所示。

由圖6可以看出,不同子帶得到的空間譜效果不同,少數(shù)子帶得到的空間譜中有兩個(gè)譜峰,很多子帶僅有一個(gè)譜峰,這是因?yàn)閮蓚€(gè)寬帶信號(hào)頻率基本無重疊,在100 Hz頻率附近,含有兩個(gè)信號(hào)的頻率成分,這些子帶能較準(zhǔn)確地估計(jì)出兩個(gè)譜峰,而遠(yuǎn)離100 Hz頻率處的子帶,僅包含一個(gè)信號(hào)的頻率成分,故得到的空間譜中僅有一個(gè)譜峰。
4.2ISM與EWISM算法的比較
實(shí)驗(yàn)條件:同上,采用EWISM算法進(jìn)行DOA估計(jì),得到每個(gè)子帶的空間譜和加權(quán)后的空間譜如圖7所示。
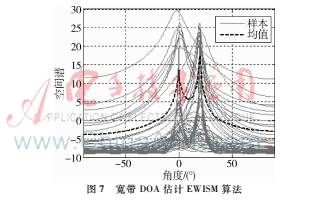
EWISM對(duì)不同子帶的DOA估計(jì)結(jié)果進(jìn)行了不同的加權(quán)處理,信噪比越高的子帶權(quán)重越高,信噪比越低的子帶權(quán)重越低,得到的空間譜的分辨力更高,估計(jì)結(jié)果更準(zhǔn)確,如圖7所示,經(jīng)過加權(quán)后的EWISM算法優(yōu)于傳統(tǒng)的ISM算法。
4.3ETISM算法的仿真及分析
實(shí)驗(yàn)條件:同上,采用ETISM算法進(jìn)行DOA估計(jì),其中能量門限選擇為個(gè)子帶能量的均值,實(shí)驗(yàn)結(jié)果如圖8所示。
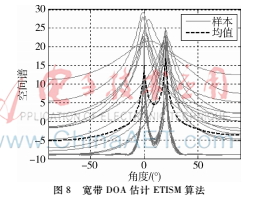
ETISM算法通過對(duì)子帶進(jìn)行篩選,選出了信噪比較高的子帶進(jìn)行DOA估計(jì),舍棄了信噪比低的那些子帶,減少了計(jì)算量,提高了DOA估計(jì)的精度。
4.4三種算法對(duì)不同寬帶信號(hào)DOA估計(jì)
選擇兩組不同的寬帶信號(hào),一組信號(hào)頻譜無重疊,另一組信號(hào)頻譜部分重疊。
(1)頻譜無重疊
實(shí)驗(yàn)條件:兩線性調(diào)頻信號(hào)頻譜: 0~100 Hz,400~500 Hz;陣元數(shù)M=8, SNR=[10,10],陣元間距為最高頻率對(duì)應(yīng)半波長(zhǎng),信號(hào)為兩個(gè)線性調(diào)頻信號(hào),劃分子帶數(shù)目J=64,頻域快拍K=32; DOA=[0, 20];仿真結(jié)果如圖9所示。
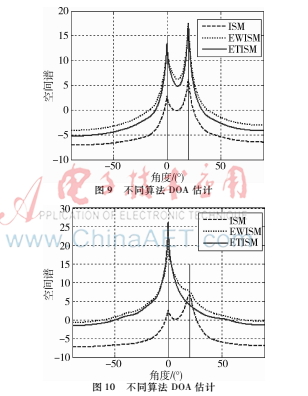
(2)信號(hào)頻譜無重疊,信號(hào)功率差距大
實(shí)驗(yàn)條件:信號(hào)頻率范圍分別為:0~50 Hz,100~600 Hz,信噪比SNR=[20,10],其他條件同上,采用三種算法進(jìn)行DOA估計(jì),結(jié)果如圖10所示。
(3)信號(hào)頻譜部分重疊
實(shí)驗(yàn)條件:信號(hào)頻率范圍分別為:100~400 Hz,200~500 Hz,SNR=[10,10],其他條件同上,采用三種算法進(jìn)行DOA估計(jì),結(jié)果如圖11所示。
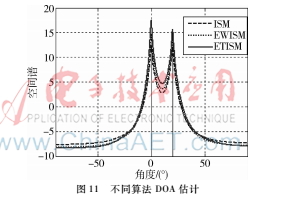
由圖9~圖11可以看出,當(dāng)兩信號(hào)頻率成分重合較多時(shí),三種算法性能基本相同。當(dāng)信號(hào)頻率無重疊且兩信號(hào)信噪比相當(dāng)時(shí),部分子帶不包含有用信號(hào)頻率,這些子帶DOA估計(jì)性能極差,若采用統(tǒng)計(jì)平均,將會(huì)影響整體性能。此時(shí)EWISM、ETISM有效地處理了上述問題,給予較小的權(quán)重或舍去相應(yīng)的子帶,效果較好。EWISM、ETISM算法優(yōu)于傳統(tǒng)的ISM算法,當(dāng)兩信號(hào)頻譜無重疊且功率差距較大時(shí),如圖10所示,由于信號(hào)1功率大,信號(hào)2功率小,EWISM對(duì)信號(hào)1的子帶加權(quán)大,對(duì)信號(hào)2子帶加權(quán)小,此時(shí)DOA估計(jì)結(jié)果偏向信號(hào)1,信號(hào)2幾乎被掩蓋。同樣,對(duì)ETISM算法,信號(hào)1的子帶被選出,信號(hào)2的子帶
被忽略,最終導(dǎo)致信號(hào)2處無法形成較好的譜峰,導(dǎo)致各算法性能均不理想,EWISM、ETISM算法均只有一個(gè)明顯的譜峰,不如傳統(tǒng)的ISM算法。為解決上述問題,可利用信號(hào)頻帶不同的特點(diǎn),先對(duì)接收數(shù)據(jù)進(jìn)行濾波處理,分別對(duì)濾波得到的信號(hào)進(jìn)行單信源的寬帶DOA估計(jì),最終聯(lián)合得到DOA估計(jì)結(jié)果。
5總結(jié)
與MUSIC算法相比,ESPRIT算法進(jìn)行DOA估計(jì)同樣具有較高的分辨力,而且不需要進(jìn)行譜峰搜索,其計(jì)算量大大減小,但其估計(jì)精度不如MUSIC算法。由窄帶信號(hào)的MUSIC算法引出了對(duì)寬帶信號(hào)的處理,針對(duì)ISM算法的運(yùn)算量大和精確度低兩點(diǎn)不足,提出了EWISM、ETISM兩種改進(jìn)算法,兩種算法克服了低信噪比子帶對(duì)DOA估計(jì)結(jié)果的影響,仿真實(shí)驗(yàn)證明了該方法的有效性。通過對(duì)不同帶寬的寬帶信號(hào)DOA估計(jì)仿真實(shí)驗(yàn),分析了各算法的不同應(yīng)用場(chǎng)合:在兩信號(hào)頻譜有重疊且功率相當(dāng)時(shí),改進(jìn)的兩種算法要明顯優(yōu)于傳統(tǒng)的ISM算法;而當(dāng)其頻譜無重疊時(shí),若信號(hào)功率相當(dāng),則ETISM、EWISM明顯優(yōu)于ISM算法,若信號(hào)功率差距較大,此時(shí)三種方法效果都不理想,改進(jìn)的算法可能不如傳統(tǒng)的ISM算法,此時(shí),可利用頻帶不重疊的特點(diǎn)進(jìn)行濾波處理,對(duì)單個(gè)寬帶信號(hào)作DOA估計(jì),最終聯(lián)合得到波達(dá)方向[6]。
參考文獻(xiàn)
[1] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas & Propagation,1986,34(3):276-280.
[2] 王永良,陳輝,彭萬寧,等.空間譜估計(jì)理論與算法研究[M].北京:清華大學(xué)出版社,2004.
[3] 張攬?jiān)?楊德森.矢量陣的非空間ESPRIT算法[J].哈爾濱工程大學(xué)學(xué)報(bào),2009,30(4):406-410.
[4] 林靜然,彭啟棕,邵懷綜,等.一種基于能量加權(quán)的陣列寬帶信號(hào)定位算法[J]. 儀器儀表學(xué)報(bào),2005,26(8):123-125.
[5] 司偉建,林晴晴.基于延時(shí)相關(guān)處理ESPRIT算法[J].系統(tǒng)工程與電子技術(shù),2012,34(3):144-146.
[6] 劉慶華,伊?xí)詵|.基于分布式任意陣列的寬帶信源定位方法研究[J].電子技術(shù)應(yīng)用,2016,42(1):82-86.

