0 引言

    感應(yīng)耦合式非接觸電能傳輸(Inductive Contactless Power Transfer，ICPT)是一種電源與負(fù)載之間沒(méi)有直接的電氣接觸能量傳輸方式，不會(huì)產(chǎn)生電火花，避免了導(dǎo)線拖拽帶來(lái)的不便，減少了有線供電存在的安全隱患^[1]。因此，ICPT在一些特殊的場(chǎng)合下有著廣泛的應(yīng)用前景，比如應(yīng)用在電動(dòng)汽車的無(wú)線充電以及在一些起重運(yùn)輸?shù)脑O(shè)備上^[2-4]。

    針對(duì)ICPT的耦合機(jī)構(gòu)，國(guó)內(nèi)外許多研究機(jī)構(gòu)對(duì)此進(jìn)行專門(mén)的研究。以新西蘭BOY T教授為首的課題組提出了一種E型耦合結(jié)構(gòu)，這種耦合結(jié)構(gòu)的初次級(jí)線圈耦合緊密、效率高、傳輸功率大^[5-6]。文獻(xiàn)[7]針對(duì)電動(dòng)汽車無(wú)線充電，為使耦合機(jī)構(gòu)提供一個(gè)較大的充電區(qū)域，設(shè)計(jì)了一種DLDD（Double Layer Double D-type）形式的耦合線圈。文獻(xiàn)[8]中又提出一種新型的耦合結(jié)構(gòu)——H型結(jié)構(gòu)，該機(jī)構(gòu)具有效率高、橫向位移范圍大和質(zhì)量輕等特點(diǎn)。以上文獻(xiàn)中均未對(duì)耦合機(jī)構(gòu)沿軌道相對(duì)運(yùn)動(dòng)時(shí)，ICPT系統(tǒng)的平穩(wěn)性進(jìn)行研究。

    本文利用ANSYS有限元軟件并設(shè)計(jì)了實(shí)驗(yàn)，最后得出在耦合機(jī)構(gòu)沿軌道相對(duì)運(yùn)動(dòng)時(shí)，ICPT系統(tǒng)能夠保持良好的平穩(wěn)性的結(jié)論。

1 沿軌道相對(duì)運(yùn)動(dòng)的耦合結(jié)構(gòu)

    本文以起重運(yùn)輸設(shè)備為背景，為了便于對(duì)比，設(shè)計(jì)并制作了兩種耦合結(jié)構(gòu)沿軌道相對(duì)運(yùn)動(dòng)的ICPT系統(tǒng)，如圖1所示，在后文分別稱為耦合機(jī)構(gòu)1和耦合機(jī)構(gòu)2，它們的幾何參數(shù)如圖2所示。兩者主要區(qū)別是，耦合機(jī)構(gòu)1的發(fā)射線圈是水平纏繞，而耦合機(jī)構(gòu)2的發(fā)射線圈是豎直纏繞。其支撐框架均為木材和有機(jī)玻璃框架，發(fā)射線圈固定在起承重作用的工字鋼梁上，接收線圈與其他所有接收裝置沿工字鋼橫梁做水平直線運(yùn)動(dòng)。因而，發(fā)射線圈與接收線圈存在長(zhǎng)距離的相對(duì)運(yùn)動(dòng)。

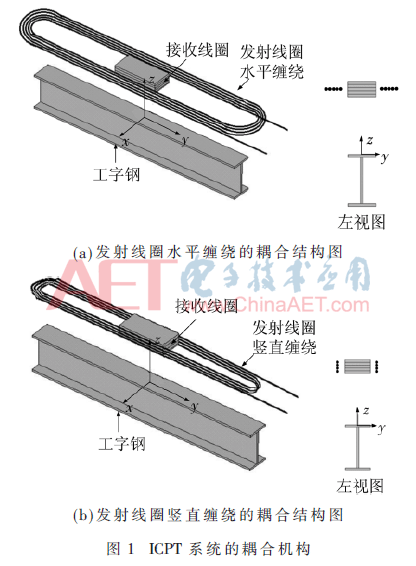
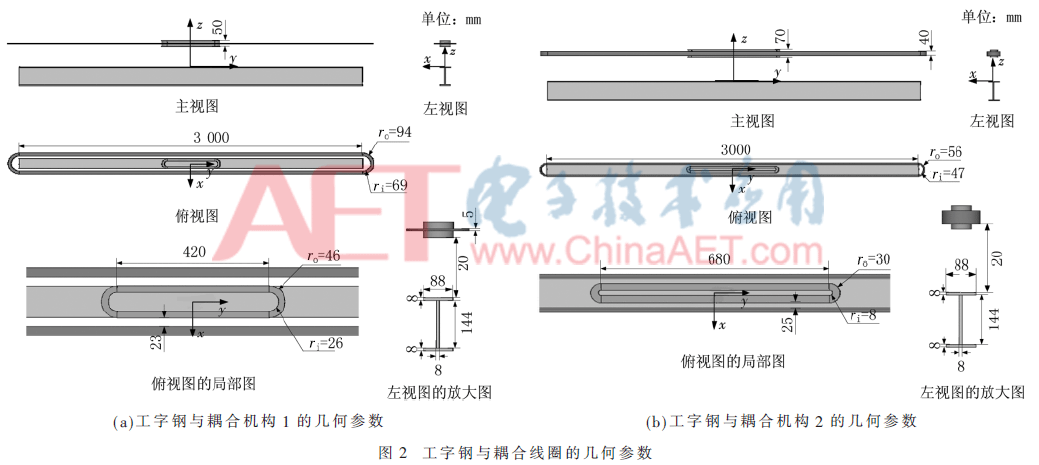
2 理論分析

2.1 耦合線圈參數(shù)的理論分析

    基于ANSYS有限元仿真得到的結(jié)果，通過(guò)ICPT系統(tǒng)的等效電路模型分析可得到耦合線圈的自感及互感。圖1中所表示的沿軌道相對(duì)運(yùn)動(dòng)耦合結(jié)構(gòu)的等效電路圖如圖3所示。

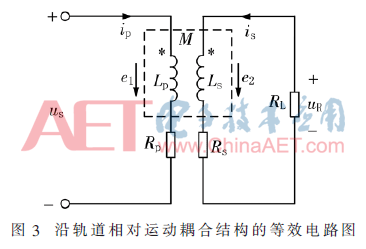
    式(2)是一個(gè)復(fù)數(shù)方程組，根據(jù)互感線圈二端口輸入、輸出能量守恒，可推出式(2)中只有3個(gè)實(shí)數(shù)方程線性無(wú)關(guān)。因此式(2)中L_p、L_s和M有唯一解。

2.2 非接觸電能傳輸系統(tǒng)的傳輸功率

    本文采用LC/S網(wǎng)絡(luò)補(bǔ)償方式，其補(bǔ)償電路圖如圖4所示，將接收端等效到發(fā)射端，再將發(fā)射端電路用諾頓電路等效，其等效電路圖如圖5所示，Z_eq為接收端等效到發(fā)射端的等效阻抗。

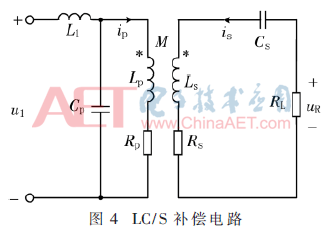
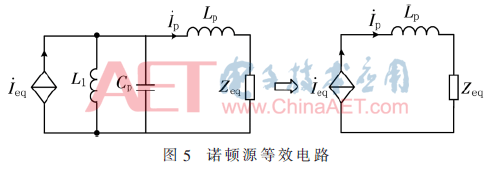
    其諾頓等效源為：

    將圖4中接收側(cè)回路用受控源回路等效，如圖6所示。

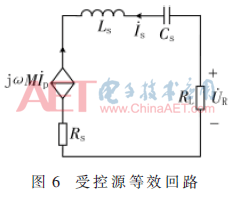
    接收側(cè)回路滿足：

    因此，ICPT系統(tǒng)的傳輸功率為：

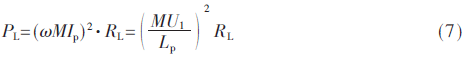
3 耦合機(jī)構(gòu)的仿真結(jié)果

    本文使用通用電磁場(chǎng)仿真工具ANSYS有限元軟件，對(duì)上述這兩種耦合機(jī)構(gòu)進(jìn)行仿真。設(shè)定耦合機(jī)構(gòu)中發(fā)射線圈距工字鋼距離d=20 cm，電源電壓U_s=351 V，負(fù)載電阻R_L=68 Ω，仿真中所用到的電氣參數(shù)如表1所示。工字鋼相對(duì)磁導(dǎo)率μ為4 000，電阻率為20×10^-8 Ω/m。

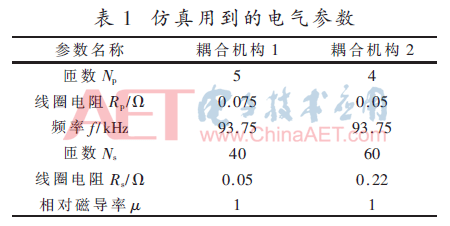
3.1 兩種耦合機(jī)構(gòu)傳輸能力的比較

    利用耦合線圈與工字鋼結(jié)構(gòu)對(duì)稱特點(diǎn)，采用其二分之一結(jié)構(gòu)模型。借用ANSYS有限元仿真軟件，得到如圖7所示耦合線圈感應(yīng)電動(dòng)勢(shì)的實(shí)部，同理，還可得到耦合線圈感應(yīng)電動(dòng)勢(shì)的虛部及負(fù)載電壓。圖7是耦合機(jī)構(gòu)1接收線圈處于中間的位置。

    因此，通過(guò)ANSYS有限元仿真可得出發(fā)射線圈和接收線圈的感應(yīng)電動(dòng)勢(shì)及負(fù)載電壓。根據(jù)第2部分的理論推導(dǎo)，可得耦合機(jī)構(gòu)線圈的自感和互感如表2所示。

    由表2可知，耦合機(jī)構(gòu)1的M₁/L_p1=0.4，耦合機(jī)構(gòu)2的M₂/L_p2=1.1，而系統(tǒng)的傳輸功率正比于M與L_p比值的平方，即耦合機(jī)構(gòu)2比耦合機(jī)構(gòu)1的傳輸能力強(qiáng)，因此，下面將對(duì)耦合機(jī)構(gòu)2沿軌道相對(duì)運(yùn)動(dòng)進(jìn)行ICPT的平穩(wěn)性研究。

3.2 耦合機(jī)構(gòu)2沿軌道相對(duì)運(yùn)動(dòng)

    下面研究耦合機(jī)構(gòu)2沿軌道相對(duì)運(yùn)動(dòng)時(shí)，ICPT功率的變化情況。分為以下3種情況：(1)接收線圈相對(duì)于發(fā)射線圈沿水平方向運(yùn)動(dòng)；(2)接收線圈相對(duì)于發(fā)射線圈在豎直方向上有偏離；(3)接收線圈在發(fā)射線圈內(nèi)前后側(cè)方向上有偏離。

    為了消除系統(tǒng)的無(wú)功損耗，減小回路阻抗，需要在接收回路中串聯(lián)補(bǔ)償電容。耦合機(jī)構(gòu)2中接收線圈的自感L_s2=667.848 μH，根據(jù)串聯(lián)諧振公式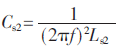：，得C_s2≈4.32 nF。由于串聯(lián)補(bǔ)償電容的影響，導(dǎo)致接收側(cè)回路中的交流電流i2的變化很大，這樣工字鋼會(huì)反過(guò)來(lái)影響耦合線圈的自感，因此根據(jù)L_s2=667.848 μH計(jì)算出來(lái)的串聯(lián)諧振電容C_s2≈4.32 nF并不是最佳的補(bǔ)償電容值。可從優(yōu)化方法的思想，根據(jù)仿真尋找出串聯(lián)補(bǔ)償電容的最優(yōu)值，其結(jié)果如表3所示。

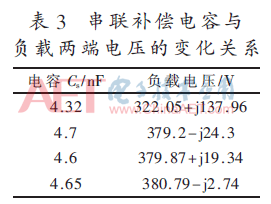
    由表3可知，接收回路中串聯(lián)補(bǔ)償電容的大小近似為4.65 nF，而實(shí)驗(yàn)中串聯(lián)補(bǔ)償電容選為4.7 nF，因此仿真中選用接收回路的串聯(lián)補(bǔ)償電容為4.7 nF。

3.2.1 接收線圈相對(duì)于發(fā)射線圈沿水平方向運(yùn)動(dòng)

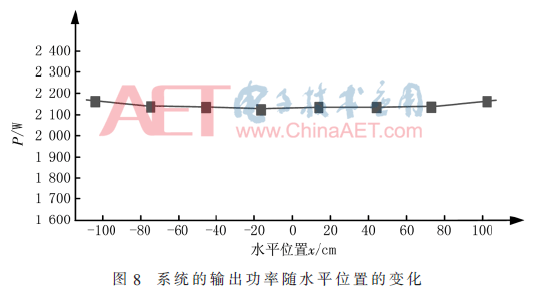
    下面仿真耦合機(jī)構(gòu)2的接收線圈沿水平方向運(yùn)動(dòng)時(shí)ICPT系統(tǒng)的平穩(wěn)性情況。記發(fā)射線圈的中心位置為原點(diǎn)O，以接收線圈在水平方向上的運(yùn)動(dòng)軌跡定為x軸，分別對(duì)接收線圈的中心位于x=±105 cm、±75 cm、±45 cm、±15 cm這8個(gè)位置仿真，得到耦合機(jī)構(gòu)2系統(tǒng)的傳輸功率隨水平位置的變化曲線如圖8所示，其中系統(tǒng)的傳輸功率的相對(duì)變化量在2%之內(nèi)。

3.2.2 接收線圈相對(duì)發(fā)射線圈在豎直方向上有偏離

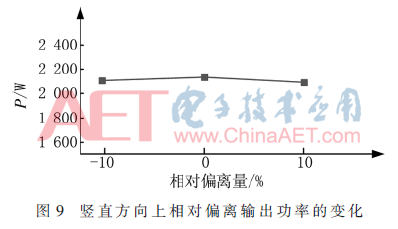
    接收線圈相對(duì)于發(fā)射線圈在豎直方向上有偏離的情況下，仿真耦合機(jī)構(gòu)2系統(tǒng)的傳輸功率的變化情況。其相對(duì)偏離量是在接收線圈的自身高度±10%內(nèi)，圖9是其傳輸功率隨偏離量的變化曲線，其中傳輸功率相對(duì)于無(wú)偏離時(shí)最大的相對(duì)變化量均不大于5%。

3.2.3 接收線圈在發(fā)射線圈內(nèi)前后側(cè)方向上有偏離

    接收線圈在發(fā)射線圈內(nèi)前后側(cè)有偏離的情況下，仿真系統(tǒng)的傳輸功率的變化情況。其相對(duì)偏離量是耦合線圈之間空隙的±20%內(nèi)，圖10是其傳輸功率隨偏離量的變化曲線。其中系統(tǒng)的傳輸功率相對(duì)于無(wú)偏離時(shí)的相對(duì)變化量均不大于2%。

    從圖8～圖10的仿真結(jié)果可知，耦合機(jī)構(gòu)2沿軌道相對(duì)運(yùn)動(dòng)時(shí)，ICPT系統(tǒng)傳輸功率的波動(dòng)范圍均在5%之內(nèi)，說(shuō)明這種耦合機(jī)構(gòu)在傳輸電能的過(guò)程中能夠保持良好的平穩(wěn)性。

4 實(shí)驗(yàn)結(jié)果

4.1 耦合線圈中自感和互感的測(cè)量

    圖11是實(shí)驗(yàn)中搭建的兩種耦合機(jī)構(gòu)的實(shí)驗(yàn)平臺(tái)，左圖是耦合機(jī)構(gòu)1實(shí)驗(yàn)裝置，右圖是耦合機(jī)構(gòu)2實(shí)驗(yàn)裝置。在接收線圈處于發(fā)射線圈的中間位置，實(shí)驗(yàn)測(cè)得這兩種耦合機(jī)構(gòu)的自感和互感如表4所示。

    將表2中的仿真值與表4中的實(shí)驗(yàn)值對(duì)比，根據(jù)誤差計(jì)算公式：誤差=可知，仿真與實(shí)驗(yàn)測(cè)量的偏差在9%之內(nèi)。

4.2 耦合機(jī)構(gòu)2沿軌道水平運(yùn)動(dòng)時(shí)測(cè)互感的實(shí)驗(yàn)

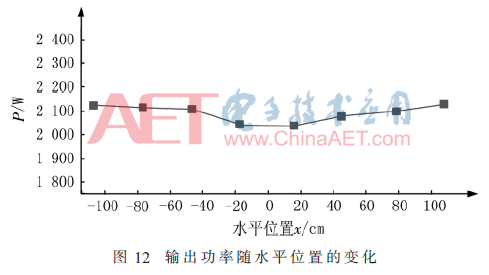
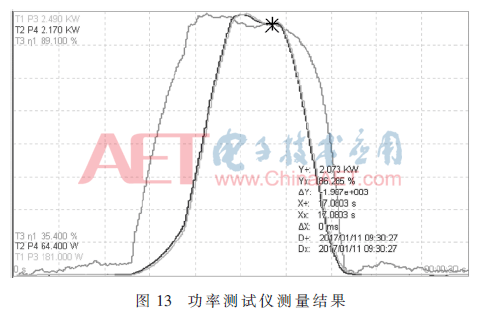
    當(dāng)接收線圈沿軌道水平運(yùn)動(dòng)時(shí)，利用PA2000mini功率測(cè)試儀對(duì)ICPT系統(tǒng)進(jìn)行測(cè)試。按照3.2.1小節(jié)中8個(gè)位置的傳輸功率進(jìn)行測(cè)量，得到的結(jié)果如圖12所示，其中傳輸功率的最大波動(dòng)在6%之內(nèi)。圖13是接收線圈運(yùn)動(dòng)到某一位置時(shí)的測(cè)量結(jié)果，圖中星號(hào)標(biāo)記點(diǎn)處系統(tǒng)的輸出功率為2.073 kW。

    實(shí)驗(yàn)結(jié)果表明，由實(shí)驗(yàn)測(cè)量到的數(shù)據(jù)與仿真數(shù)據(jù)存在一定的誤差，但數(shù)據(jù)相差不大，并且變化趨勢(shì)基本保持一致，主要原因是在仿真過(guò)程中，耦合結(jié)構(gòu)的建模采用了簡(jiǎn)化的模型。

5 結(jié)論

    借用ANSYS電磁場(chǎng)仿真軟件分析了耦合機(jī)構(gòu)沿軌道相對(duì)運(yùn)動(dòng)時(shí)，ICPT系統(tǒng)能夠保持良好的平穩(wěn)性，并通過(guò)實(shí)驗(yàn)驗(yàn)證了該結(jié)論。通過(guò)理論分析和實(shí)驗(yàn)分析發(fā)現(xiàn)，工字鋼對(duì)耦合線圈的自感確實(shí)存在一定的影響，使得在接收回路中串聯(lián)補(bǔ)償電容的理論計(jì)算值和實(shí)驗(yàn)值存在一定的差異，而利用ANSYS電磁場(chǎng)仿真軟件能夠很好地解決這一問(wèn)題。

參考文獻(xiàn)

[1] 黃學(xué)良，譚林林，陳中，等.無(wú)線電能傳輸技術(shù)研究與應(yīng)用綜述[J].電工技術(shù)學(xué)報(bào)，2013，28(10)：1-11.

[2] BUDHIA M，COVIC G A，BOYS J T.Design and optimisation of magnetic structures for lumped Inductive Power Transfer systems[C].IEEE Energy Conversion Congress and Exposition，San Jose，CA，United states，2009：2081-2088.

[3] ELLIOTT G A J，RAABE S，COVIC G A，et al.Multiphase pickups for large lateral tolerance contactless power-transfer systems[J].IEEE Transactions on Industrial Electronics，2010，57(5)：1590-1598.

[4] 潘振方，陳希有，牟憲民，等.以電動(dòng)機(jī)為負(fù)載的非接觸供電技術(shù)[J].電工技術(shù)學(xué)報(bào)，2016，31(s1)：16-24.

[5] COVIC J T B G A，REEN A W G.Stability and control of inductively coupled power transfer systems[J].IEE Proceedings-Electric Power Applications，2000，147(1)：37-43.

[6] GREEN A W，BOYS J T.10 kHz inductively coupled power transfer-concept and control[C].International Conference on Power Electronics and Variable-Speed Drives，London，UK，1994：694-699.

[7] 王智慧，胡超，孫躍，等.基于輸出能效特性的IPT系統(tǒng)耦合機(jī)構(gòu)設(shè)計(jì)[J].電工技術(shù)學(xué)報(bào)，2015，30(19)：26-31.

[8] 鄭穎楠，陳紅，張西恩.非接觸電能傳輸系統(tǒng)的松耦合變壓器實(shí)驗(yàn)研究[J].電工電能新技術(shù)，2011，30(1)：64-68.

作者信息:

楊  杰，陳希有，李冠林，吳茂鵬

（大連理工大學(xué) 電氣工程學(xué)院，遼寧 大連116024）