0  引言

云計(jì)算環(huán)境下任務(wù)調(diào)度算法的執(zhí)行效率直接影響到用戶對(duì)服務(wù)質(zhì)量的體驗(yàn),，而多數(shù)傳統(tǒng)的優(yōu)化算法已經(jīng)不能滿足現(xiàn)在的需求，因此許多研究學(xué)者提出了蟻群算法,、遺傳算法等啟發(fā)式智能類(lèi)的算法,。本文主要研究的是智能算法中的粒子群優(yōu)化（Particle Swarm Optimization,，PSO）算法,。粒子群算法的模型就是在一塊區(qū)域里讓距離食物最近的一只鳥(niǎo)去尋找食物，減少尋找時(shí)間,，提高速率,。PSO算法由于具有參數(shù)少、計(jì)算效率高,、搜索快速,、編程容易且應(yīng)用廣泛等特點(diǎn)，從而被許多學(xué)者應(yīng)用于云計(jì)算環(huán)境下任務(wù)調(diào)度算法的研究上,。

許多專(zhuān)家和學(xué)者不斷分析和研究影響任務(wù)調(diào)度的因素,，已經(jīng)在此算法上研究出許多有價(jià)值的方案。文獻(xiàn)［1］通過(guò)分析粒子飛行軌跡提出廣義和狹義中心粒子的雙中心粒子群優(yōu)化算法,，改善粒子算法的精度和收斂速度,。文獻(xiàn)［2］在滿足用戶多任務(wù)服務(wù)質(zhì)量的要求下，提出一種多QoS約束離散粒子群的優(yōu)化算法,。文獻(xiàn)［3］將混合粒子群算法結(jié)合Pareto最優(yōu)工作流調(diào)度解集合,，解決沖突的三目標(biāo)優(yōu)化問(wèn)題,。文獻(xiàn)［4］提出一種反向?qū)W習(xí)和局部學(xué)習(xí)的粒子群優(yōu)化算法，通過(guò)反向?qū)W習(xí)增加種群粒子的多樣性,，降低算法局部最優(yōu)的情況,。文獻(xiàn)［5］通過(guò)自適應(yīng)地調(diào)整慣性權(quán)重來(lái)平衡算法的全局收斂性和收斂速度，提高算法性能,。

優(yōu)化粒子群算法通常也會(huì)與其他粒子群算法相結(jié)合,。文獻(xiàn)［6］利用遺傳算法中交、變異的特點(diǎn),，將遺傳算法與改進(jìn)的粒子群算法相混合,，增強(qiáng)了粒子的變異能力，又提高了粒子的搜索精度,，大大降低了任務(wù)完成時(shí)間,。文獻(xiàn)［7］結(jié)合粒子群算法和蟻群算法各自的優(yōu)點(diǎn)，用粒子群算法使粒子群前期迭代產(chǎn)生的優(yōu)良粒子生成初始信息素,，再將信息素應(yīng)用于蟻群算法上,，最后得到最優(yōu)解。

本文首先分析粒子群算法的基本原理和粒子群在解決任務(wù)調(diào)度問(wèn)題時(shí)的缺點(diǎn),，針對(duì)缺點(diǎn),，對(duì)粒子群算法在慣性權(quán)重上進(jìn)行改進(jìn)，解決算法在前期出現(xiàn)“早熟”和后期收斂精度低的問(wèn)題,，并加入混沌擾動(dòng),，通過(guò)給出的適應(yīng)度函數(shù)，以不同任務(wù)數(shù)為研究對(duì)象,，對(duì)比算法任務(wù)完成總時(shí)間,，并觀察迭代次數(shù)的情況。

1  粒子群算法介紹

1.1 粒子群優(yōu)化算法基本原理

傳統(tǒng)粒子群優(yōu)化算法是由美國(guó)心理學(xué)家KENNEDY J和電氣工程師EBERHART RC于1995年根據(jù)魚(yú)群,、鳥(niǎo)群覓食的活動(dòng)提出的一種智能化算法^［8］,。但傳統(tǒng)粒子群優(yōu)化算法不存在對(duì)粒子運(yùn)動(dòng)速度的調(diào)整，使算法對(duì)局部搜索和全局搜索的能力降低,。因此為了彌補(bǔ)傳統(tǒng)粒子群優(yōu)化算法的不足,，SHI Y和EBERHART R C在此算法的前提下引入了慣性權(quán)重，并深入研究,，使粒子的運(yùn)動(dòng)速度不再是單一固定不變的速度^［9-10］,。

粒子群中的所有粒子都有自己的位置、運(yùn)動(dòng)方向和速度,。每個(gè)粒子都是一個(gè)個(gè)體,，粒子本身在經(jīng)歷多次迭代后出現(xiàn)的個(gè)體最優(yōu)解叫做個(gè)體極值pbest，群粒子組成的群體會(huì)出現(xiàn)全局最優(yōu)解,，即全局極值gbest,。所有的粒子都會(huì)尋找最佳位置,，就是說(shuō)粒子會(huì)向最優(yōu)解進(jìn)行搜索，這是由優(yōu)化函數(shù)的一個(gè)適應(yīng)值決定的,。PSO算法首先要初始化粒子群,，然后粒子通過(guò)在個(gè)體最優(yōu)解和全局最優(yōu)解反復(fù)更新自己的位置和速度，經(jīng)過(guò)反復(fù)迭代,，最終得到極值,。

記粒子群中粒子個(gè)數(shù)為N，粒子在d維空間運(yùn)動(dòng),，則k時(shí)刻粒子i的位置和速度公式如下,。

由優(yōu)化函數(shù)適應(yīng)值決定粒子個(gè)體最優(yōu)位置和全局最優(yōu)位置的公式如下。

個(gè)體最優(yōu)位置：

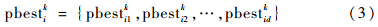
全局最優(yōu)位置：

在取得兩個(gè)極值之前,，粒子會(huì)根據(jù)如下公式進(jìn)行搜索,，更新位置和速度：

其中，d為粒子搜索空間維數(shù),；k為迭代次數(shù),，也指當(dāng)前時(shí)刻下；c_1,，c₂為兩個(gè)正常數(shù),，即學(xué)習(xí)因子，也叫加速因子,；α,、β是兩個(gè)介于0和1之間的隨機(jī)數(shù)。

ω為慣性權(quán)重,，SHI Y和EBERHART R C將慣性權(quán)重引入粒子群算法中,，即

ω=ω_max－(ω_max－ω_min)×k/K_max (7)

其中， ω_max,、ω_min分別是最大和最小慣性權(quán)重,， k為此刻粒子迭代次數(shù),，K_max為粒子最大迭代次數(shù),。

根據(jù)標(biāo)準(zhǔn)粒子群算法原理，影響PSO算法的主要參數(shù)有：粒子群規(guī)模,、慣性權(quán)重,、學(xué)習(xí)因子及粒子運(yùn)動(dòng)的最快速度等。

1.2 粒子群算法的應(yīng)用及問(wèn)題

PSO算法已經(jīng)被廣泛應(yīng)用于解決多目標(biāo)問(wèn)題,、動(dòng)態(tài)優(yōu)化,、參數(shù)優(yōu)化、組合優(yōu)化等各類(lèi)優(yōu)化問(wèn)題,，以及應(yīng)用于模糊系統(tǒng)控制,、電力分配系統(tǒng),、神經(jīng)網(wǎng)絡(luò)、流水車(chē)間調(diào)度,、生物醫(yī)學(xué)等各領(lǐng)域中,。但是用在云計(jì)算環(huán)境解決任務(wù)調(diào)度的優(yōu)化問(wèn)題時(shí)，會(huì)出現(xiàn)陷入局部最優(yōu),、后期收斂速度慢等問(wèn)題,；與其他啟發(fā)類(lèi)智能算法一樣，這一種算法不可能解決所有的優(yōu)化問(wèn)題,。PSO算法較適用于解決連續(xù)化的問(wèn)題上對(duì)于任務(wù)調(diào)度這個(gè)離散型問(wèn)題不能夠很好地發(fā)揮其優(yōu)勢(shì),，因此需要在PSO算法的基礎(chǔ)上進(jìn)一步改進(jìn)算法性能，以去除算法在任務(wù)調(diào)度過(guò)程中存在的弊端,，從而取得更好的實(shí)際效果,，改善資源利用率和平臺(tái)的服務(wù)質(zhì)量，提高用戶體驗(yàn),。

2  改進(jìn)型粒子群算法研究

在現(xiàn)實(shí)應(yīng)用中,，算法的優(yōu)化提高不可能只是單方面的，通常情況下都是多個(gè)目標(biāo)優(yōu)化問(wèn)題,，但是多目標(biāo)優(yōu)化多數(shù)情況下是互相矛盾,、存在沖突的，所以最好的優(yōu)化只能是根據(jù)實(shí)際情況,，權(quán)衡各個(gè)目標(biāo)而得到相對(duì)的極值,。本文以任務(wù)完成時(shí)間為算法性能優(yōu)劣的主要依據(jù)。

2.1 適應(yīng)度函數(shù)

粒子需要通過(guò)適應(yīng)值判斷當(dāng)前位置的優(yōu)劣,。任務(wù)調(diào)度就是用最短的時(shí)間最高效率地完成任務(wù),，完成任務(wù)時(shí)間越小，目標(biāo)函數(shù)值就越大,，種群中粒子的適應(yīng)度就越好,。因此首先要定義適應(yīng)度函數(shù)，并將式（1）中xkid代入適應(yīng)函數(shù)f（x）,，求適應(yīng)值,。

設(shè)有 r個(gè)資源，s個(gè)粒子,，任務(wù)i在資源j上的執(zhí)行時(shí)間用T(i,j)表示：

完成任務(wù)的總時(shí)間為：

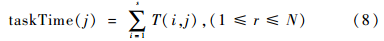
定義適應(yīng)度函數(shù)為: 

2.2 慣性權(quán)重的計(jì)算

PSO算法在解決任務(wù)調(diào)度問(wèn)題時(shí)容易出現(xiàn)的問(wèn)題就是前期陷入局部最優(yōu),，后期全局的搜索精度降低。所以為了平衡全局和局部搜索能力,，在相關(guān)研究中權(quán)重的改進(jìn)包括自適應(yīng)權(quán)重,、隨機(jī)權(quán)重等。本文采用指數(shù)形式的慣性權(quán)重ω的改進(jìn)方法。慣性權(quán)重ω的取值較大,，全局的搜索能力會(huì)提高,，但局部的搜索能力會(huì)變差；若ω取值較小,，算法的局部搜索能力會(huì)提高,，但是全局的搜索能力不佳。根據(jù)慣性權(quán)重存在的問(wèn)題,，本文將慣性權(quán)重的表達(dá)式改進(jìn)為：

ω=ω_min+exp［－((ω_max－ω_min)×k/K_max)²］                   (10) 

由上式可知,，式中ω會(huì)以指數(shù)的形式在迭代前期保持一個(gè)較大的值，從而使粒子群在迭代前期全局搜索能力增強(qiáng),；在迭代后期ω能夠保持一個(gè)較小且變化平緩的值,，提高算法后期局部的搜索能力，加快收斂速度,。依據(jù)前人相關(guān)研究,，本文慣性權(quán)重取值范圍為［0.4~0.9］。

2.3 混沌擾動(dòng)

混沌在一定范圍內(nèi)可以等概率無(wú)重復(fù)遍歷所有狀態(tài),，算法在解決任務(wù)的過(guò)程中,，其他粒子會(huì)因?yàn)榉N群中極少數(shù)最優(yōu)粒子的引導(dǎo)向最優(yōu)粒子迅速靠近，如果此粒子并沒(méi)有達(dá)到全局最優(yōu),，則有可能導(dǎo)致算法陷入局部最優(yōu),。混沌對(duì)粒子初始值敏感,，能夠依據(jù)混沌的內(nèi)部規(guī)則,，隨機(jī)地遍歷所有的粒子。所以為了避免粒子陷入“早熟”時(shí),，需要加入一個(gè)外部擾動(dòng),，讓粒子可以打破局部最優(yōu)。

當(dāng)粒子發(fā)生早熟時(shí)要存在一個(gè)外部擾動(dòng)機(jī)制使粒子群跳出“早熟”,。本文采用的混沌擾動(dòng)公式為：

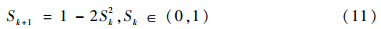
算法實(shí)現(xiàn)流程如圖1所示,。

圖 1  算法的實(shí)現(xiàn)流程圖

3  實(shí)驗(yàn)仿真與分析

本實(shí)驗(yàn)使用云計(jì)算工具Cloudsim-3.0作為實(shí)驗(yàn)平臺(tái)，MyEclipse為開(kāi)發(fā)工具,，Java為開(kāi)發(fā)語(yǔ)言,。實(shí)驗(yàn)基本流程為：搭建實(shí)驗(yàn)環(huán)境，初始化Cloudsim,，創(chuàng)建數(shù)據(jù)中心,、服務(wù)代理,，設(shè)置虛擬機(jī)資源及任務(wù)的參數(shù),，擴(kuò)展并調(diào)用任務(wù)調(diào)度算法，啟動(dòng)Cloudsim，最后進(jìn)行實(shí)驗(yàn)結(jié)果分析,。

3.1 仿真實(shí)驗(yàn)過(guò)程

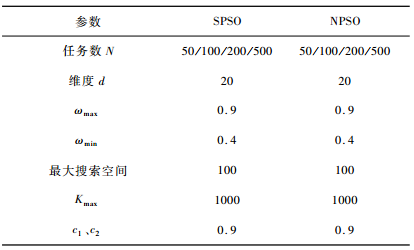
用Cloudsim部署實(shí)驗(yàn)環(huán)境,，在DatacenterBroker中擴(kuò)展新算法，將任務(wù)數(shù)分別設(shè)置為50,，100,200,500,，實(shí)驗(yàn)將改進(jìn)后的算法與標(biāo)準(zhǔn)粒子群算法（SPSO）進(jìn)行實(shí)驗(yàn)仿真，并對(duì)這兩個(gè)算法在任務(wù)完成時(shí)迭代次數(shù)的情況進(jìn)行分析對(duì)比,。文中提出的算法的參數(shù)設(shè)置如表1所示,。

表1  SPSO和改進(jìn)后算法的參數(shù)設(shè)置

3.2 實(shí)驗(yàn)結(jié)果比較及討論

根據(jù)表1設(shè)置實(shí)驗(yàn)參數(shù)，為保證實(shí)驗(yàn)的準(zhǔn)確性,，每組實(shí)驗(yàn)進(jìn)行20次,，最后取20次實(shí)驗(yàn)的平均值進(jìn)行比較分析。實(shí)驗(yàn)比較兩種算法在任務(wù)數(shù)不同時(shí),，完成時(shí)間最短時(shí)的迭代次數(shù)的情況,，實(shí)驗(yàn)結(jié)果對(duì)比如圖2~5所示。

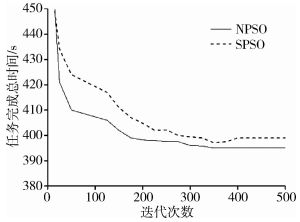
圖 2  任務(wù)數(shù)為50時(shí)的任務(wù)總完成時(shí)間

圖 3  任務(wù)數(shù)為100時(shí)的任務(wù)總完成時(shí)間

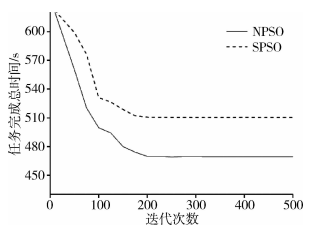
圖 4  任務(wù)數(shù)為200時(shí)的任務(wù)總完成時(shí)間

圖 5  任務(wù)數(shù)為500時(shí)的任務(wù)總完成時(shí)間

通過(guò)上述實(shí)驗(yàn)結(jié)果對(duì)比可以得出,，在迭代前期NPSO算法比SPSO算法收斂能力更強(qiáng),，但是在任務(wù)數(shù)相同時(shí)NPSO算法比NPSO算法完成任務(wù)所用的總時(shí)間有所減少，且后期的收斂性較強(qiáng),，通過(guò)對(duì)比可知,，改進(jìn)后的算法有更好的執(zhí)行效率，在實(shí)際應(yīng)用中能更好地改善用戶的使用體驗(yàn),。

4  結(jié)論

許多研究人員針對(duì)任務(wù)調(diào)度算法開(kāi)展了許多相關(guān)研究,，本文在前人的基礎(chǔ)上對(duì)標(biāo)準(zhǔn)粒子群算法進(jìn)行進(jìn)一步進(jìn)行改進(jìn)。通過(guò)優(yōu)化慣性權(quán)重,，并且在粒子群算法的過(guò)程中加入混沌擾動(dòng),，遍歷粒子狀態(tài)，根據(jù)給出的適應(yīng)度函數(shù),，對(duì)新算法的性能與其他任務(wù)調(diào)度算法進(jìn)行對(duì)比,。實(shí)驗(yàn)結(jié)果表明，本文方案有效地降低了任務(wù)執(zhí)行時(shí)間,，降低了資源消耗成本,，具有可行性。

參考文獻(xiàn)

 ［1］ 湯可宗, 柳炳祥, 楊靜宇,等. 雙中心粒子群優(yōu)化算法［J］. 計(jì)算機(jī)研究與發(fā)展, 2012, 49(5):1086-1094.

［2］ Wang Yue, Liu Yaqiu, Guo Jifeng,et al.QoS scheduling algorithm in cloud computing based on discrete particle swarm optimization［J］.Computer Engineering,2017,43(6) : 111-117.

［3］ 杜艷明,肖建華.云環(huán)境中基于混合多目標(biāo)粒子群的科學(xué)工作流調(diào)度算法［J］.計(jì)算機(jī)科學(xué),2017,44(8):252-259.

［4］ 夏學(xué)文,劉經(jīng)南,高柯夫,等.具備反向?qū)W習(xí)和局部學(xué)習(xí)能力的粒子群算法［J］.計(jì)算機(jī)學(xué)報(bào),2015,38(7):1397-1407.

［5］ 任圓圓,，劉培玉,，薛素芝. 一種新的自適應(yīng)動(dòng)態(tài)文化粒子群優(yōu)化算法［J］. 計(jì)算機(jī)應(yīng)用研究，2013, 30(11):3240-3243.

［6］ 王波,張曉磊.基于粒子群遺傳算法的云計(jì)算任務(wù)調(diào)度研究［J］.計(jì)算機(jī)工程與應(yīng)用,2015,51(6):84-88.

［7］ 王登科,李忠.基于粒子群優(yōu)化與蟻群優(yōu)化的云計(jì)算任務(wù)調(diào)度算法［J］.計(jì)算機(jī)應(yīng)用與軟件,2013,30(1):290-293.

［8］ KENNEDY J, EBERHART R C. Particle swarm optimization［C］//Proceedings of IEEE Conference on Neural Networks, Perth, Australia, 1995:1942-1948.

［9］ SHI Y, EBERHART R. Modified particle swarm optimizer［C］// Proceedings of IEEE ICEC Conference, Anchorage, 1998:69-73.

［10］ EBERHART R C, SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization［C］// Proceedings of the 2000 Congress on Evolutionary Computation, 2000.  IEEE, 2002:84-88.

（收稿日期：2018-04-14）

作者簡(jiǎn)介：

許向陽(yáng)（1967-）,，男,，碩士,，副教授，主要研究方向：信息網(wǎng)絡(luò)管理,。

張芳磊（1990-）,，女，碩士研究生,，主要研究方向：信息網(wǎng)絡(luò)管理,。