0 引言

    在如今數(shù)字技術(shù)中，半帶濾波器因其通帶阻帶對(duì)稱,，系數(shù)具有偶對(duì)稱性且濾波器階數(shù)為奇數(shù),，有效系數(shù)少等特點(diǎn)廣泛應(yīng)用于通信、視頻處理,、語音識(shí)別等數(shù)字信號(hào)處理應(yīng)用中,，尤其常用于實(shí)現(xiàn)信號(hào)的2倍抽取。對(duì)于一個(gè)階數(shù)為N(N為偶數(shù)),，長度為N+1的半帶濾波器,，傳統(tǒng)的多相分解技術(shù)下實(shí)現(xiàn)2倍抽取功能的轉(zhuǎn)置實(shí)現(xiàn)結(jié)構(gòu)如圖1所示,。

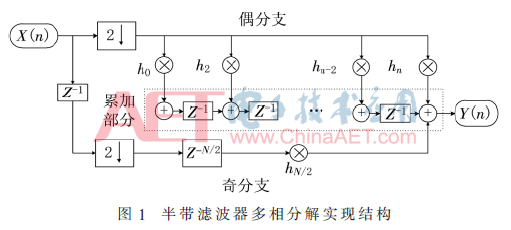
    首先，利用多相分解^[1],，濾波運(yùn)算分為奇偶兩個(gè)分支進(jìn)行,，輸入數(shù)據(jù)經(jīng)過2倍抽取后得到偶分支上的濾波輸入；輸入數(shù)據(jù)經(jīng)過一個(gè)延遲單位進(jìn)行2倍抽取后得到奇分支上的輸入數(shù)據(jù),。偶分支上共有偶數(shù)個(gè)系數(shù)且系數(shù)對(duì)稱,。對(duì)于偶分支上數(shù)據(jù)乘以各系數(shù)的操作可以稱為多常數(shù)乘法(Multiple Constant Multiplications，MCM),，眾所周知乘法器的硬件實(shí)現(xiàn)會(huì)消耗大量的資源,，故可采用以移位相加代替偶分支濾波運(yùn)算過程中的所有乘法操作以節(jié)省硬件資源。

    一般的移位相加實(shí)現(xiàn)方法是對(duì)系數(shù)進(jìn)行正則有符號(hào)數(shù)(Canonic Signed Digit,，CSD)編碼^[2],，以減少硬件資源開銷，根據(jù)文獻(xiàn)[1],，基于CSD編碼的方式比二進(jìn)制編碼方式平均減少33%的硬件開銷,。同時(shí)偶分支的濾波結(jié)構(gòu)還可以采用混合形式，降低累加部分中加法器的開銷^[3],。

    不同于傳統(tǒng)使用CSD編碼的辦法,，本文采用的是利用以2r為基礎(chǔ)數(shù)的算法(RADIX-2r)實(shí)現(xiàn)MCM操作。傳統(tǒng)CSD編碼的方法是對(duì)每個(gè)系數(shù)進(jìn)行編碼,，每個(gè)系數(shù)的乘法是獨(dú)立的,，無法共享硬件資源。而RADIX-2r算法中,，利用系數(shù)之間共享基本表達(dá)式以達(dá)到共享硬件資源的目的,，必然比傳統(tǒng)辦法節(jié)省硬件資源。

1 所設(shè)計(jì)半帶濾波器的參數(shù)

    本文中所設(shè)計(jì)的兩個(gè)半帶濾波器分別為歸一化頻率下過渡帶帶寬為6/11,、阻帶衰減大于90 dB和過渡帶帶寬為1/11、阻帶衰減大于90 dB,。設(shè)計(jì)可通過MATLAB軟件完成^[4],，具體實(shí)現(xiàn)代碼如下所示：

    h1=halfband(‘Type’，’Lowpass’,，6/11,90),；

    Hb1=design(h1，’equiripple’),；

    h2=halfband(‘Type’,，’Lowpass’，1/11,90),；

    Hb2=design(h2,，’equiripple’),；

    由MATLAB軟件仿真可得，寬過渡帶半帶濾波器階數(shù)為18,，窄過渡帶半帶濾波器階數(shù)為118,，要達(dá)到90 dB阻帶衰減的技術(shù)指標(biāo)，寬過渡帶半帶濾波器系數(shù)量化位數(shù)為17位,，窄過渡帶半帶濾波器系數(shù)量化位數(shù)為21位,。

    系數(shù)量化后兩個(gè)濾波器的幅頻響應(yīng)分別如圖2、圖3所示,。如圖所示,，所得半帶濾波器均滿足阻帶衰減大于90 dB的設(shè)計(jì)指標(biāo)。量化后的寬過渡帶半帶濾波器的有效系數(shù)如表1所示,，窄過渡帶半帶濾波器量化后的系數(shù)如表2所示,。

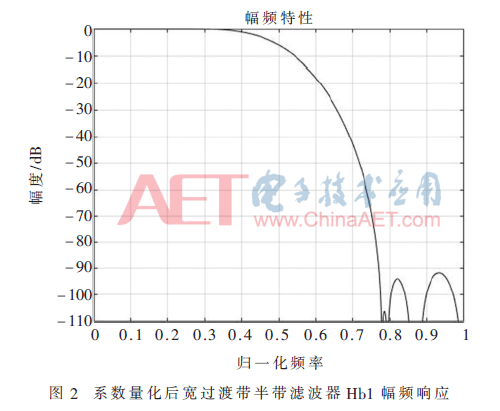
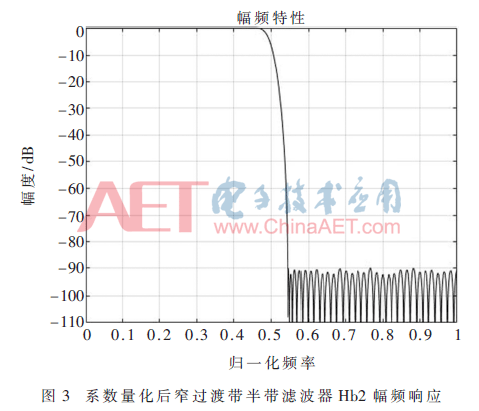
    從表1中可見，寬過渡帶半帶濾波器的有效系數(shù)只有11個(gè),，其中,，多相分解下，奇分支上的有效系數(shù)只有h(9),，其余全為偶分支上的有效系數(shù)且具有對(duì)稱性,。

    同理從表2中得知，窄過渡帶半帶濾波器的有效系數(shù)為61個(gè),，奇分支上只有一個(gè)有效系數(shù)h(59),，其余全為偶分支上的系數(shù)且具對(duì)稱性。

2 高效實(shí)現(xiàn)方法

    傳統(tǒng)的CSD編碼實(shí)現(xiàn)方式下是對(duì)每個(gè)有效系數(shù)進(jìn)行CSD編碼然后用移位相加操作完成乘法,，將消耗大量的硬件資源,。與使用CSD編碼不同的是，本文提出了使用RADIX-2^r算法實(shí)現(xiàn)偶分支濾波運(yùn)算中的MCM,，達(dá)到以更低功耗,、更小面積實(shí)現(xiàn)半帶濾波的目的。

2.1 RADIX-2r算法實(shí)現(xiàn)MCM

    一個(gè)N-bit常數(shù)C在RADIX-2^r算法中由式(1)表示：

    MCM模塊中,，輸入X將同時(shí)乘以擁有M個(gè)常數(shù)的常數(shù)集{C₀,，C₀，…,，C_M-2,，C_M-1}。常數(shù)集中需要由MCM模塊產(chǎn)生乘積的數(shù)只有正的奇數(shù),，因?yàn)榕紨?shù)可以通過奇數(shù)進(jìn)行左移操作獲得,，而負(fù)數(shù)可以通過正數(shù)取負(fù)獲得，如常數(shù)積-132X可以通過常數(shù)積33X左移2位并取負(fù)獲得,，在MCM問題中只需實(shí)現(xiàn)33X即可,，不需要用多余的加法器實(shí)現(xiàn)-132X,。常數(shù)集中所需實(shí)現(xiàn)的正的奇數(shù)被稱為基本數(shù)。根據(jù)文獻(xiàn)[5],、[6]可知,，相比于現(xiàn)有的研究，RADIX-2r算法是實(shí)現(xiàn)MCM模塊最好的辦法,，在功耗,、面積、速度上都具有顯著的優(yōu)勢(shì),。

    對(duì)于本文中半帶濾波器Hb1的偶分支的實(shí)現(xiàn),，通過RADIX-2r算法可以得到其基本部分積為{1，3,，5,，7}，需要實(shí)現(xiàn)的基本數(shù)集為{57,，101,，1 601，4 985,，20 115}基本部分積的具體實(shí)現(xiàn)過程如下所示：

    X1=X

    X3=X1<<1+X1

    X5=X1<<2+X1

    X7=X1<<3-X1

    基本數(shù)集的實(shí)現(xiàn)過程如下所示：

    X57=X1<<6-X7

    X101=X5+X3<<5

    X1601=X1+X1<<6+X3<<9

    X4985=X1<<12+X7<<7-X7

    X20115=X3-X7<<4-X1<<8+X5<<12

　　同理對(duì)于半帶濾波器Hb2,，偶分支中的基本部分積與基本數(shù)集分別如下所示：

    由于篇幅原因，半帶濾波器Hb2基本部分積與基本數(shù)集的實(shí)現(xiàn)過程不在此列出,。

2.2 寄存基本部分積以降低功耗

    數(shù)字電路在工作時(shí),，主要的功耗來自于動(dòng)態(tài)功耗，而動(dòng)態(tài)功耗中大部分為數(shù)字單元基本門電路的開關(guān)行為導(dǎo)致,。由文獻(xiàn)[7]可知,，擁有長路徑的加法器將會(huì)導(dǎo)致更活躍的開關(guān)行為，這是因?yàn)橛刹煌舆t路徑引起的無用毛刺將沿著路徑從MCM模塊傳播至后續(xù)的累加模塊中,。雖然這種毛刺不會(huì)產(chǎn)生任何電路上的邏輯錯(cuò)誤,，但數(shù)字電路中高達(dá)70％的開關(guān)活動(dòng)是由這些毛刺造成，進(jìn)而會(huì)造成比較大的功耗,。

    因而,，有效降低功耗的方法即是減少電路中因延遲不同而產(chǎn)生的毛刺。根據(jù)前文所述使用RADIX-2r實(shí)現(xiàn)MCM模塊的方法中,，每一個(gè)基本數(shù)的實(shí)現(xiàn)都可以通過基本部分積之間的移位相加操作完成,。本文所提出的另一降低功耗的方法是寄存MCM模塊中產(chǎn)生的基本部分積的輸出,，通過使用邊沿有效的寄存器可以有效地消除毛刺,，因?yàn)榧拇嫫髦辉诖_定的時(shí)鐘邊沿進(jìn)行采值，阻斷毛刺從MCM模塊向累加部分的傳播,，進(jìn)而減少電路的開關(guān)行為,。同時(shí)因?yàn)榛静糠址e的數(shù)目總是遠(yuǎn)小于基本數(shù)的總數(shù),，所以相比于寄存基本數(shù)，寄存基本部分積不會(huì)帶來太多的額外寄存器的開銷,。對(duì)于文中Hb1半帶濾波器而言,，即是寄存X1、X3,、X5,、X7四個(gè)數(shù)值。

2.3 所提出的半帶濾波器實(shí)現(xiàn)結(jié)構(gòu)

    本文提出的Hb1半帶濾波器的總體實(shí)現(xiàn)方法如圖4所示,，使用了表1中的系數(shù),。總體結(jié)構(gòu)包含三個(gè)子部分,，一是多相分解部分,；二是利用RADIX-2^r實(shí)現(xiàn)MCM部分，其中包括了對(duì)基本部分積的寄存,；最后是濾波運(yùn)算的累加部分,，此部分中還采取奇支路和偶支路積共用寄存器的策略。因篇幅原因,，Hb2的實(shí)現(xiàn)結(jié)構(gòu)圖不在此展出,。

3 實(shí)驗(yàn)結(jié)果及分析

    為了評(píng)測本文提出的應(yīng)用于數(shù)字信號(hào)抽取下的半帶濾波器的實(shí)現(xiàn)方法的性能，對(duì)于文中的半帶濾波器Hb1,、Hb2,，分別用Verilog HDL硬件描述語言實(shí)現(xiàn)了傳統(tǒng)的CSD編碼結(jié)構(gòu)、CSD編碼下的混疊結(jié)構(gòu)以及本文所提出的結(jié)構(gòu),。在邏輯綜合結(jié)果方面進(jìn)行比較,。

    綜合使用的軟件為Synopsys公司的Design Compiler軟件，使用的工藝庫為TSMC 40 nm工藝,，并設(shè)置濾波器的輸入字長為16 bit,。表3、表4分別展示了Hb1,、Hb2不同方案所需要的硬件資源,。

    功耗分析使用的時(shí)鐘頻率為200 MHz，兩個(gè)濾波器每個(gè)方案綜合后的結(jié)果如表5,、表6所示,。

    通過以上表中數(shù)據(jù)可知，文獻(xiàn)[3]所提出的實(shí)現(xiàn)方法相較于CSD編碼的實(shí)現(xiàn)方法不具有優(yōu)勢(shì),，僅在實(shí)現(xiàn)窄過渡帶濾波器時(shí)降低了濾波器的面積,，但提升效果也十分有限。而本文所提出的實(shí)現(xiàn)方法相對(duì)于傳統(tǒng)CSD編碼實(shí)現(xiàn)結(jié)構(gòu)在功耗及面積表現(xiàn)上均有明顯優(yōu)勢(shì)，對(duì)于寬過渡帶半帶濾波器,，在本文的實(shí)現(xiàn)方法中,，功耗下降了9.36%，面積下降了6.31%,；對(duì)于窄過渡帶半帶濾波器,，本文的實(shí)現(xiàn)方法使功耗降低了13.93%，面積降低了12.79%,。

4 結(jié)論

    本文針對(duì)應(yīng)用于數(shù)字信號(hào)下變頻技術(shù)中的半帶濾波器,，提出了一種低功耗的實(shí)現(xiàn)方法。利用MATLAB軟件設(shè)計(jì)半帶濾波器,，并對(duì)新的實(shí)現(xiàn)方法進(jìn)行了Modelsim仿真驗(yàn)證,，最后由Design Complier 軟件進(jìn)行綜合。結(jié)果表明,，與傳統(tǒng)的CSD編碼實(shí)現(xiàn)方法相比較,，本文提出的實(shí)現(xiàn)方法能有效地降低濾波器的功耗與面積，具有較高的實(shí)用價(jià)值,，可廣泛應(yīng)用工程需求中的半帶濾波器的實(shí)現(xiàn),。

參考文獻(xiàn)

[1] 卜祥元，方金輝,，范星宇,，等.基于抽取濾波器多相分解的多速率采樣模塊設(shè)計(jì)[J].北京理工大學(xué)學(xué)報(bào)，2014(2)：187-191.

[2] GOEL N,，NANDI A.Design of FIR filter using FCSD representation[C].IEEE International Conference on Computational Intelligence and Communication Technology,，2015：617-620.

[3] LOU X，MEHER P K,，YU Y,，et al.Novel structure for area-efficient implementation of FIR filters[J].IEEE Transactions on Circuits and Systems，2017,，64：1212-1216.

[4] 杜勇.數(shù)字濾波器的MATLAB與FPGA實(shí)現(xiàn)[M].北京：電子工業(yè)出版社,，2015.

[5] OUDJIDA A，LIACHA A,，BAKIRI M,，et al.Multiple constant multiplication algorithm for high-speed and low-power design[J].IEEE Transactions on Circuits and Systems，2016,，63(2)：176-180.

[6] LIACHA A,，OUDJIDA A，F(xiàn)ERGUENE F,，et al.Design of high-speed,，low-power,，and area-efficient FIR filers[J].IET Circuits，Devices & Systems,，2018，12(1)：1-11.

[7] YE W B,，YU Y J.Switching activity analysis and power estimation for multiple constant multiplier block of FIR filters[C].IEEE International Symposium of Circuits and Systems,，2011：145-148.

作者信息:

徐  鵬

(電子科技大學(xué) 電子科學(xué)與工程學(xué)院，四川 成都610054)