0 引言
SPWM(Sinusoidal PWM)控制技術(shù)是逆變器研究和應(yīng)用領(lǐng)域的核心技術(shù)之一，在早期的SPWM實現(xiàn)方法中,，最典型的是由一個模擬比較器對一個三角載波和一個正弦調(diào)制信號進(jìn)行比較,，實現(xiàn)正弦調(diào)制信號對三角載波的調(diào)制。這種將三角載波和正弦調(diào)制波進(jìn)行實時比較實現(xiàn)調(diào)制的方法叫作自然采樣法,。顯然,，自然采樣法適合于用模擬比較電路來實現(xiàn)。模擬電路實現(xiàn)簡單,、響應(yīng)速度快,，但是存在著參數(shù)漂移大、集成度低和設(shè)計不靈活等同有而又難以克服的缺點,。
上世紀(jì)80年代以來,，隨著計算機技術(shù)的快速發(fā)展，基于微控制器的運用方案得到了迅速的發(fā)展,，運用單片機,、DSP等器件實現(xiàn)SPWM成為主流，最常用的是各種形式的規(guī)則采樣法,，但是在某些特殊的場合：如在高頻大功率,、低失真逆變電源中,，常用的規(guī)則采樣法無法滿足要求。
因此,，如何改進(jìn)SPWM算法以提高逆變電源的各項指標(biāo)成為值得長期深入研究的課題之一,。隨著微電子技術(shù)的飛速發(fā)展，特別是FPGA的集成度的大大提高(芯片內(nèi)部提供大量的硬件乘法器),，使得復(fù)雜算法在系統(tǒng)中得到簡單快速的解決,。文獻(xiàn)提出了一種改進(jìn)的面積等效算法，進(jìn)行了諧波仿真分析,。文獻(xiàn)論述了用DSP與FPGA相結(jié)合來實現(xiàn)基于規(guī)則采樣法的多路SPWM波形發(fā)生器,。文獻(xiàn)提出了數(shù)字化自然采樣法，并用FPGA實現(xiàn)SPWM波形,。
本文提出了規(guī)則采樣線性外推的準(zhǔn)自然采樣SPWM方法(以下簡稱線性外推法),，該方法利用模數(shù)轉(zhuǎn)換器(ADC)對正弦調(diào)制波有規(guī)律地在每個三角載波周期內(nèi)波峰和波谷采樣，將得到的相鄰的兩個采樣點連線并延長外推,，此直線必然與三角載波相交,，得出求解SPWM開關(guān)點的通式。該方法近似替代了自然采樣法,，使用FPGA的硬件乘法器可快速地實現(xiàn)開關(guān)點通式的計算,，進(jìn)一步求出脈沖的寬度、間隔時間及單個載波周期內(nèi)的SPWM波形的基本算法,。本文主要闡述了線性外推法的基本算法及該方法與自然采樣法,、規(guī)則采樣法的比較。結(jié)果表明：線性外推法改進(jìn)了規(guī)則采樣法,，達(dá)到了逼近自然采樣法的調(diào)制效果,，諧波分析效果明顯
l 線性外推法
l.1 基本思想
三角載波與正弦調(diào)制波如圖l所示。a,、b為規(guī)則采樣法的開關(guān)點,，SPWM1為其對應(yīng)的SPWM波形;c、d為自然采樣法的開關(guān)點,，SPWM2為其對應(yīng)的SPWM波形,。
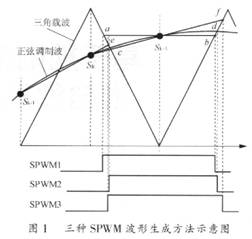
線性外推法的基本原理是：在每一個三角載波的波峰和波谷處分別采樣，然后將相鄰兩個采樣點連線并延長,，則延長線必定與三角載波相交于一點,，由此點作為開關(guān)點決定SPWM波形。圖l假設(shè)任意的第K個采樣點為波峰采樣,，記為Sk,，則住其前后的兩個采樣點都為波谷采樣，分別記為Sk-1和Sk+1,。Sk-1與Sk+1的線性外推的交點為e,，Sk與Sk+1的線性外推的交點為f,，SPWM3為其對應(yīng)的SPWM波形。
從以上三種方法實現(xiàn)的SPWM波形可以看出,，采用線性外推方法求得的開關(guān)點比規(guī)則采樣法更接近自然采樣法的開關(guān)點,。
1.2 開關(guān)點求解
本文介紹在雙極型調(diào)制時,線性外推法開關(guān)點的求解方法。
圖2是任意單個開關(guān)周期開關(guān)點示意圖,，圖2中T為載波周期,，Sk-1、Sk,、Sk+1為相鄰三個采樣點,，a、b為開關(guān)點,。線性外推法決定的SPWM開關(guān)點有如下規(guī)律：當(dāng)前波峰處采樣點與其前一個波谷處采樣點線性外推,，得到的開關(guān)點決定開關(guān)器件的導(dǎo)通時刻，此時SPWM的脈沖輸出高電平;當(dāng)前波谷處采樣點與其前一個波峰處采樣點線性外推,，得到的開關(guān)點決定開關(guān)器件的關(guān)斷時刻,，此時SPWM的脈沖輸出低電平。
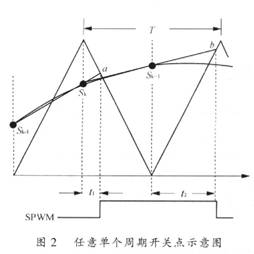
由圖2可知,，開關(guān)點應(yīng)為
其導(dǎo)通時間為
為載波周期,。根據(jù)其周期性的特點，其開關(guān)點的通式為
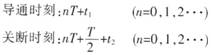
下文推導(dǎo)t1,、t2(均大于零)的求解公式,。
設(shè)三角載波的正、負(fù)峰值為B和一B值,，載波周期為T,，則雙極式三角載波斜率可表示為
本文研究的是雙極型調(diào)制時的線性外推法，在建立坐標(biāo)系時,，正弦調(diào)制波和三角載波同時向上平移B。圖3是求解開關(guān)時刻的數(shù)學(xué)模型示意圖,。分別建立如下坐標(biāo)系,，此時求解開關(guān)點時.三角載波方程可以在所屬的坐標(biāo)系中進(jìn)行簡化。
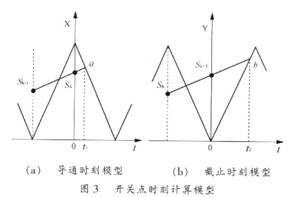
由t1和t2的值和開關(guān)點的通式就可以得到整個SPWM波形
2 仿真研究
2.l 波形仿真
在雙極型條件下,，使用自編的Matlab函數(shù)y1=xinsuanfa(Ur,，B，sf1,，mm,，cf)進(jìn)行仿真研究。其中,，Ur為正弦調(diào)制波的單峰值,，B為三角載波的峰值,，sf1為調(diào)制波的頻率，mm是一個和計算THD相關(guān)的整數(shù)系數(shù),，它表示計算THD時,，最高次諧波計算到第mm次載波及其邊帶，cf為三角載波的頻率,。圖4是調(diào)制度為0.8,，載波比為5的仿真結(jié)果。圖4中的上半部分是正弦調(diào)制波與三角載波,，可以看出SPWM調(diào)制的載波比與調(diào)制度,。下半部分為三種調(diào)制方法實現(xiàn)的三個SPWM波形，依次是①對應(yīng)規(guī)則采樣法,、②對應(yīng)自然采樣法,、③對應(yīng)線性外推法。
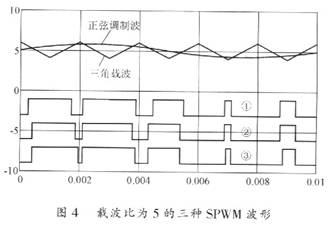
線性外推法的特點是由當(dāng)前最后兩個采樣點的線性外推近似,。因此,，在正弦調(diào)制波的正半部分，兩采樣點決定的直線的斜率,，在增區(qū)間必定大于正弦調(diào)制波本身,，在減區(qū)間必定小于正弦調(diào)制波本身，此時決定的SPWM波的導(dǎo)通時刻必定在自然采樣導(dǎo)通時刻的左邊,，而SPWM波的關(guān)斷時刻必定在自然采樣關(guān)斷時刻的右邊;在正弦調(diào)制波的負(fù)半部分,，兩采樣點決定直線的斜率，在減區(qū)間必定大于正弦調(diào)制波本身,，在增區(qū)間必定小于正弦調(diào)制波本身,，此時決定的SPWM波的導(dǎo)通時刻必定在自然采樣導(dǎo)通時刻的右邊，而SPWM波的關(guān)斷時刻必定在自然采樣關(guān)斷時刻的左邊,。
使用新方法得到的SPWM序列逼近了自然采樣法的SPWM序列,，且在正弦調(diào)制波的正方向，自然采樣法SPWM的導(dǎo)通段包含在新算法SPWM的導(dǎo)通段中,，負(fù)方向恰恰相反,。這恰好與上面的分析一致。
2.2 諧波分析
線性外推法與自然采樣法相比,，不同點在于線性外推法是用兩采樣點的外推直線近似替代正弦曲線,，再與三角載波進(jìn)行比較。因此,，用新方法求得的交點的幅值總是大于自然采樣交點的幅值,。在調(diào)制度為0.8的條件下，載波比分別為7、25和71時的諧波分析如圖5所示,。在一定范圍內(nèi)隨著載波比的增大,，基波幅值有效值從大變小，越來越接近理想的調(diào)制波幅值,。
圖6是在調(diào)制度分別為0.8,、0.5和0.3下的基波幅值隨載波比的變化曲線，圖6中③對應(yīng)本文新方法,、②對應(yīng)自然采樣法,、①對應(yīng)規(guī)則采樣法。從圖6中可以看出三束曲線分別都向給定的調(diào)制度逼近,。由丁本方法是線性外推,，因此，基波的輸出幅值最高;每束的第一根曲線都是呈下降趨勢,，隨著載波比的增大,，線性外推法得到的開關(guān)點越接近自然采樣法的開關(guān)點，基波幅值呈下降趨勢,，得到的仿真曲線與前而的分析一致,。隨著載波比大到一定的范圍，正弦波在三角載波周期內(nèi)可以近似用直線替代,，因此,，三種方法趨于一致。
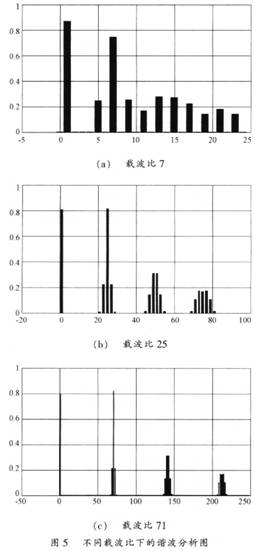
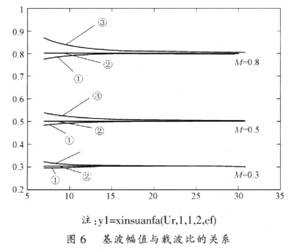
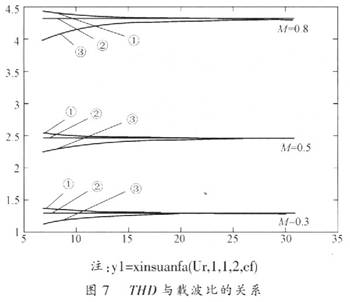
圖7是調(diào)制度分別為0.8,、0.5和0.3對應(yīng)的THD隨載波比變化曲線,。三根曲線分別為③對應(yīng)本文新放法、②對應(yīng)自然采樣法,、①對應(yīng)規(guī)則采樣法,，根據(jù)THD的基本計算公式，得到仿真結(jié)果,。三種方法的THD仿真結(jié)果表明,，新方法的THD指標(biāo)最優(yōu)，隨著載波比的增大,，三種方法的THD趨于一致,。
3 結(jié)語
(1)提出了一種線性外推的新方法，該算法相對簡單,，易于實現(xiàn)。
(2)仿真結(jié)果表明,，該方法在載波比大范圍變化時,，輸出基波幅值和輸出THD兩項指標(biāo)均優(yōu)于自然采樣法和規(guī)則采樣法的這兩項指標(biāo)。隨著載波比N的增大(一定范圍內(nèi))，各項指標(biāo)都趨于一致,。