雙足機(jī)器人相比于一般的移動(dòng)機(jī)器人在非結(jié)構(gòu)化環(huán)境中具有更好的移動(dòng)能力，因而受到研究者的廣泛關(guān)注^[1],?？刂茩C(jī)器人獲得快速的行走速度以及實(shí)現(xiàn)跑動(dòng)步態(tài)仍然是雙足機(jī)器人領(lǐng)域中具有挑戰(zhàn)性的問題之一。機(jī)器人快速行走或跑動(dòng)時(shí),，擺動(dòng)腳在落地的瞬間會(huì)產(chǎn)生一個(gè)較大的沖擊力,，此力使落地腳反彈或使零力矩點(diǎn)(zero moment point)產(chǎn)生較大跳變，從而造成機(jī)器人穩(wěn)定裕度降低和跌倒,。這種現(xiàn)象被稱為沖擊效應(yīng),，它是制約雙足機(jī)器人提高步行速度和跑步的因素。
　　氣動(dòng)人工肌肉是近年來發(fā)展起來的一種新型的驅(qū)動(dòng)器,，McKibben型氣動(dòng)肌肉是其中應(yīng)用最為廣泛的一種,。它具有柔順、功率/質(zhì)量比大,、在力/長(zhǎng)度特性上與人類肌肉類似等優(yōu)點(diǎn),。由于其具有柔順性可控的優(yōu)點(diǎn)，應(yīng)用氣動(dòng)人工肌肉作為驅(qū)動(dòng)器可以有效地解決雙足機(jī)器人的落地腳沖擊問題,。因此,，將氣動(dòng)人工肌肉作為雙足機(jī)器人的驅(qū)動(dòng)器具有良好的前景。但是,，人工肌肉具有高度非線性的特點(diǎn),，并伴隨有遲滯現(xiàn)象,，使得對(duì)其建模和控制困難。目前,，基于氣動(dòng)人工肌肉的雙足機(jī)器人的研究剛剛起步,，只有少數(shù)幾個(gè)雙足機(jī)器人項(xiàng)目對(duì)此進(jìn)行了研究。本文利用McKibben氣動(dòng)人工肌肉搭建了類似生物頡頏關(guān)節(jié)的單自由度人工關(guān)節(jié),。此系統(tǒng)的硬件部分包括氣壓驅(qū)動(dòng)子系統(tǒng),、傳感器子系統(tǒng)和控制子系統(tǒng)。在此硬件系統(tǒng)上構(gòu)建了軟件系統(tǒng),，實(shí)現(xiàn)了對(duì)此人工關(guān)節(jié)軌跡的跟蹤控制,。基于本文的工作可以進(jìn)一步研究和解決氣動(dòng)人工肌肉及關(guān)節(jié)的建模和控制問題,，為設(shè)計(jì)和搭建基于氣動(dòng)人工肌肉驅(qū)動(dòng)器的雙足機(jī)器人打下基礎(chǔ),。
1 氣動(dòng)人工肌肉關(guān)節(jié)系統(tǒng)軟硬件設(shè)計(jì)
1.1 氣動(dòng)人工肌肉
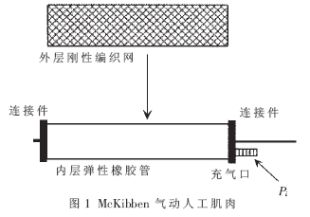
　　McKibben氣動(dòng)人工肌肉是由美國(guó)醫(yī)生Joseph. L. McKibben發(fā)明并以其名字命名的一種柔性氣動(dòng)驅(qū)動(dòng)器。McKibben氣動(dòng)人工肌肉的主體主要由外層編織網(wǎng)和內(nèi)層彈性橡膠管組成,其結(jié)構(gòu)如圖1所示,。

　　圖1為肌肉結(jié)構(gòu)圖,，其中，Pi為輸入氣壓,，其大小由控制器根據(jù)實(shí)際工作情況進(jìn)行控制,。當(dāng)輸入端氣壓Pi增大時(shí), 內(nèi)層橡膠管膨脹,由于外層編織網(wǎng)剛度很大，幾乎不能伸長(zhǎng), 限制肌肉只能徑向變形(直徑變大,，長(zhǎng)度縮短),，產(chǎn)生軸向收縮力;而當(dāng)輸入端氣壓Pi降低時(shí),導(dǎo)致人工肌肉伸長(zhǎng)(松馳) ,肌肉的剛度及驅(qū)動(dòng)力也就隨之降低。肌肉的剛度可通過控制橡膠管內(nèi)的氣壓實(shí)現(xiàn)^[2],，這種肌肉具有變剛度特性,，可等效為一只變剛度的彈簧。
1.2 單自由度關(guān)節(jié)系統(tǒng)
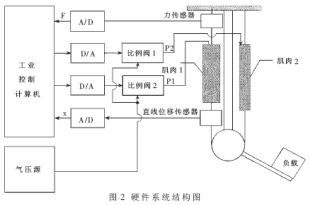
　　由于氣動(dòng)人工肌肉只能提供單向驅(qū)動(dòng)力,，故需由兩條肌肉以類似生物頡頏肌的方式構(gòu)成對(duì)抗性回轉(zhuǎn)關(guān)節(jié)以實(shí)現(xiàn)操作臂的力閉合,。本文利用McKibben氣動(dòng)人工肌肉作為驅(qū)動(dòng)器搭建了單自由度頡頏關(guān)節(jié)系統(tǒng)。此系統(tǒng)的硬件部分由氣壓驅(qū)動(dòng)子系統(tǒng),、傳感器子系統(tǒng)和控制子系統(tǒng)組成,。系統(tǒng)結(jié)構(gòu)圖如圖2所示。

1.2.1 氣壓驅(qū)動(dòng)子系統(tǒng)
　　氣壓驅(qū)動(dòng)子系統(tǒng)由氣源,、壓力伺服比例閥,、McKibben氣動(dòng)人工肌肉及機(jī)構(gòu)部分組成。由氣源提供壓力為0.6~0.9MPa的壓縮氣體,，壓縮氣體由導(dǎo)管經(jīng)過伺服比例閥送入氣動(dòng)人工肌肉中,。每條肌肉均與一伺服比例閥相連并有一出氣閥門和一進(jìn)氣閥門。通過控制伺服比例閥上所加的電壓即可控制肌肉中的氣體壓力,。加壓后的氣動(dòng)肌肉輸出收縮張力并驅(qū)動(dòng)機(jī)構(gòu)部分的關(guān)節(jié)轉(zhuǎn)動(dòng),，因此通過對(duì)肌肉壓力的控制即可達(dá)到軌跡跟蹤所需的關(guān)節(jié)力矩,。本系統(tǒng)中采用的McKibben氣動(dòng)人工肌肉為FESTO公司的MAS-20-300N型，其工作壓力范圍為0~0.6MPa,，最大工作頻率為3Hz,，最大收縮為肌肉長(zhǎng)度的25%，0.6MPa時(shí)理論作用力為300N,，重復(fù)精度小于1%,。壓力伺服比例閥接受控制端傳入的電壓輸入并通過調(diào)節(jié)充氣閥門和進(jìn)氣閥門控制肌肉內(nèi)氣壓。本系統(tǒng)采用了SMC公司的ITV005C-2ML型壓力比例閥,。此閥的輸入范圍為0~5VDC,，輸出為0.001~0.9MPa之間的壓力。
1.2.2 傳感器子系統(tǒng)
　　傳感器子系統(tǒng)由力傳感器和直線位移傳感器構(gòu)成,。通過直線位移傳感器可以測(cè)量出肌肉的收縮量,，根據(jù)此收縮量可以利用肌肉和關(guān)節(jié)模型進(jìn)行軌跡跟蹤控制。力傳感器測(cè)量肌肉拉力,，根據(jù)此拉力與關(guān)節(jié)力矩的線性關(guān)系可以計(jì)算出關(guān)節(jié)力矩,，從而完成關(guān)節(jié)的伺服閉環(huán)控制。本系統(tǒng)中采用的力傳感器是航天科技集團(tuán)公司701所的BK-2F型高精度S形測(cè)力/稱重傳感器,。其測(cè)量作用力的最大范圍可達(dá)80kg,，精度為0.05%,。輸出經(jīng)過TS-2型放大器放大后,，輸出電壓范圍為-5V~+5V。直線位移傳感器采用了WDL型直滑式導(dǎo)電塑料電位計(jì),。
1.2.3 控制子系統(tǒng)
　　控制子系統(tǒng)由工業(yè)控制計(jì)算機(jī)(IPC),、A/D" title="A/D">A/D采集卡、D/A轉(zhuǎn)換卡組成,。軟件控制系統(tǒng)運(yùn)行于工業(yè)控制計(jì)算機(jī)上,，并通過D/A轉(zhuǎn)換器將數(shù)字控制量轉(zhuǎn)換為模擬量。此模擬量用以控制壓力伺服比例閥的輸出氣壓,。A/D轉(zhuǎn)換器采集拉力傳感器和直線位移傳感器的數(shù)據(jù),，并提供給工業(yè)控制計(jì)算機(jī)可由軟件處理的數(shù)字信號(hào)。本系統(tǒng)中采用的D/A轉(zhuǎn)換器為PCL-726型6通道模擬量輸出卡,。它提供了6個(gè)12位雙緩沖的模擬量輸出通道,，可滿足肌肉伺服控制的需要。A/D采集卡采用了PCL-813B型12位32通道A/D卡,，它提供了32通道帶隔離的直流電壓測(cè)量,，精度可以滿足系統(tǒng)要求,。
1.3 軟件系統(tǒng)
　　氣動(dòng)人工肌肉驅(qū)動(dòng)的頡頏關(guān)節(jié)中有2條肌肉的壓力為系統(tǒng)的控制變量,。由于系統(tǒng)通過2個(gè)自由變量控制一個(gè)自由度的運(yùn)動(dòng),，所以構(gòu)成了冗余驅(qū)動(dòng)系統(tǒng)?？梢宰C明,，此系統(tǒng)可對(duì)關(guān)節(jié)力矩與關(guān)節(jié)剛度進(jìn)行獨(dú)立控制。其中,，前者與2條肌肉壓力差有關(guān),，后者與肌肉壓力和有關(guān)^[3]。通過對(duì)關(guān)節(jié)力矩的控制可以實(shí)現(xiàn)精確的關(guān)節(jié)軌跡跟蹤,，而通過對(duì)關(guān)節(jié)剛度的控制可以降低落地腳沖擊及系統(tǒng)能耗,。
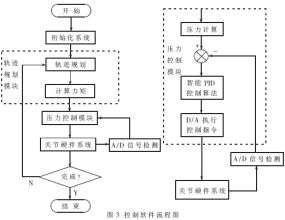
　　本文在工控計(jì)算機(jī)中編寫了氣動(dòng)人工肌肉關(guān)節(jié)系統(tǒng)的控制軟件及操作界面。通過此軟件系統(tǒng)可以實(shí)現(xiàn)肌肉模型的參數(shù)設(shè)定,、穩(wěn)定的閉環(huán)控制及傳感器返回值的實(shí)時(shí)顯示和記錄等功能,。軟件的主體部分包括軌跡規(guī)劃模塊和壓力控制模塊。軌跡規(guī)劃模塊實(shí)現(xiàn)了上層的關(guān)節(jié)軌跡規(guī)劃,，并根據(jù)關(guān)節(jié)模型計(jì)算實(shí)現(xiàn)期望關(guān)節(jié)軌跡所需的關(guān)節(jié)力矩,。壓力控制模塊執(zhí)行底層計(jì)算，它的輸入量為上層規(guī)劃得到的期望關(guān)節(jié)力矩,。壓力計(jì)算模塊根據(jù)氣動(dòng)人工肌肉的實(shí)際模型計(jì)算控制肌肉運(yùn)動(dòng)所需壓力,，其輸出為期望肌肉壓力值。智能PID控制算法模塊根據(jù)此期望壓力值和A/D采集得到的實(shí)際肌肉壓力數(shù)據(jù)進(jìn)行智能PID控制,，從而實(shí)現(xiàn)閉環(huán)控制,。其輸出經(jīng)數(shù)值和D/A環(huán)節(jié)轉(zhuǎn)換為輸出到硬件系統(tǒng)的實(shí)際控制電壓。軟件系統(tǒng)的框圖如圖3所示,。

2 實(shí)驗(yàn)及系統(tǒng)應(yīng)用
2.1 氣動(dòng)關(guān)節(jié)系統(tǒng)模型
　　為了實(shí)現(xiàn)對(duì)本文所搭建的氣動(dòng)人工肌肉驅(qū)動(dòng)頡頏關(guān)節(jié)的準(zhǔn)確伺服控制,，首先要對(duì)氣動(dòng)人工肌肉進(jìn)行建模。McKibben氣動(dòng)人工肌肉由于具有非線性,、時(shí)變特性,，并且在工作時(shí)伴隨有遲滯現(xiàn)象，因而難于對(duì)其進(jìn)行建模和控制,。大多數(shù)已有研究中對(duì)于McKibben氣動(dòng)人工肌肉的建模都采用Chou和Hannaford^[4]基于虛功原理給出的理論模型,。此模型給出了肌肉出力的理想估計(jì)，然而此理論模型直接應(yīng)用于實(shí)際控制并不能得到良好的效果,。本研究中采用了Reynolds等^[5]提出的三元肌肉動(dòng)力學(xué)模型,，將氣動(dòng)肌肉近似為由非線性阻尼因子、非線性彈簧因子和非線性收縮力因子并聯(lián)構(gòu)成的動(dòng)力學(xué)系統(tǒng),，則模型方程為：
　　F=F₀+F₁p+(K₀+K₁p)x+(B₀+B₁p)x　　　　　　(1)
　　其中,，x為肌肉收縮長(zhǎng)度，當(dāng)肌肉完全伸張時(shí)x=0。K0,、K1為彈簧因子系數(shù),，B0、B1為阻尼因子系數(shù),，F(xiàn)0,、F1為收縮力因子。對(duì)于本文采用的氣動(dòng)人工肌肉,，通過在本系統(tǒng)上的實(shí)驗(yàn),，可對(duì)式(1)中的三元肌肉模型參數(shù)進(jìn)行準(zhǔn)確估計(jì)。當(dāng)肌肉壓力p取值在200kPa～650kPa之間時(shí),，通過實(shí)驗(yàn)得到的模型系數(shù)可得到滿意的近似效果,。應(yīng)用此三元肌肉模型，本文所介紹的軟件系統(tǒng)對(duì)關(guān)節(jié)進(jìn)行了閉環(huán)軌跡跟蹤控制,，其控制精度優(yōu)于傳統(tǒng)的理論模型,。
2.2 系統(tǒng)應(yīng)用
　　在本文構(gòu)建的采用柔性驅(qū)動(dòng)器McKibben氣動(dòng)人工肌肉作為驅(qū)動(dòng)源的機(jī)器人單自由度頡頏關(guān)節(jié)系統(tǒng)上，可對(duì)McKibben型氣動(dòng)人工肌肉的建模和控制進(jìn)行進(jìn)一步的研究,。通過在本系統(tǒng)上的實(shí)驗(yàn),，在對(duì)三元肌肉模型參數(shù)進(jìn)行準(zhǔn)確估計(jì)的基礎(chǔ)上，利用本文實(shí)現(xiàn)的控制軟件系統(tǒng)可實(shí)現(xiàn)了閉環(huán)的關(guān)節(jié)軌跡跟蹤控制,。
　　在進(jìn)一步工作中,，將基于已有的平臺(tái)和閉環(huán)控制方法重點(diǎn)研究?jī)蓚€(gè)問題。首先研究關(guān)節(jié)剛度可控的軌跡跟蹤控制,。利用此冗余系統(tǒng)的關(guān)節(jié)剛度量實(shí)現(xiàn)優(yōu)化的目的,，使機(jī)器人通過更好地利用自身關(guān)節(jié)的被動(dòng)動(dòng)力學(xué)特性來降低能量損耗。其次研究在有沖擊情況下通過控制關(guān)節(jié)剛度降低沖擊影響,，進(jìn)而為搭建由氣動(dòng)肌肉驅(qū)動(dòng)的雙足機(jī)器人提供理論準(zhǔn)備,。
參考文獻(xiàn)
1 Huang Q. Planning walking patterns for a biped robot.IEEE transactions on robotics and automation,2001;17(3):280~289
2 楊 鋼,李寶仁,劉 軍.一種新型氣動(dòng)執(zhí)行元件－氣動(dòng)人工肌肉.中國(guó)機(jī)械工程, 2003;14(15):pp:1347~1349
3 Verrelst B. A dynamic walking biped actuated by pleated pneumatic artificial muscles. PhD thesis, Vrije Universiiteit Brussel, 2005
4 Chou C P,， Hannaford B. Measurement and modeling of Mckibben pneumatic artificial mus-cle. IEEE Transaction on robotics and autom-ation, 1996;12(1):90~103
5 Reynolds D B, Repperger D W, Phillips C，A et al.Modeling the dynamic characteristics of pneumatic muscle.Annals of biomedical engin-eering, 2003;31:310~317