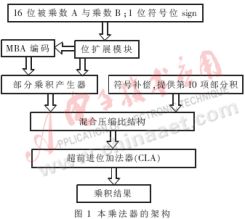
乘法是數字信號處理中的基本運算。在圖像,、語音,、加密等數字信號處理領域中，乘法器扮演著重要的角色,，并在很大程度上左右著系統(tǒng)的性能,。如何以最少的資源實現乘法器的最高速度將成為乘法器的主要研究方向。由于樹型結構模塊是陣列乘法器設計中的瓶頸,，本文在深入研究了乘法器的體系結構,，并比較了各種樹型結構的基礎之上,，提出了一種適合于16×16有/無符號數乘法器的混合壓縮比結構。并且基于該結構同時采用改進布斯算法,、符號擴展技術設計出了一個16×16有/無符號數乘法器,，其架構如圖1所示。

1 改進布斯算法與布斯編碼設計
　　在高速乘法器的設計中廣泛應用的是改進布斯算法(Modified Booth Algorithm, MBA),，也稱為基4(Radix-4)布斯算法,。該算法通過對乘數重新編碼和壓縮部分乘積項" title="乘積項">乘積項(PP)的數目來提高運算速度。而壓縮率則取決于編碼方法,，如果采用三位MBA編碼,，則可以壓縮一半的PP^[1]，大大提高了運算速度,。
　　MBA編碼原理如下：對于有符號數乘法運算A×B,，若乘數B的長度為奇數，則需要高位擴展一位符號位使乘數的位數是偶數,；若乘數B的長度為偶數則不用高位擴展,。設擴展后乘數B的長度為N位，這時N是偶數,，乘數B可寫為：

　　這樣,，N位的乘數B將會產生N/2個部分乘積項。
　　改進布斯編碼規(guī)則是：首先對乘數的最低位額外增加一位(B_[-1]=0),，然后每次取乘數的偶數位(B[0],，B^[2]，B^[4],，… )以及相鄰的奇數位(共三位)進行編碼,。這樣E＜i＞的取值為0，±1,±2,，然后再與被乘數A相乘,，得到對應的部分乘積項是(0，＋A,，－A,，＋2A，－2A),，這五種操作需要3位的布斯狀態(tài)碼進行識別,。
　　在本設計中，布斯狀態(tài)碼所采用的邏輯關系如下：
　　PN=BH
　　ONE=(~BR)&BL∣ BR&(~BL)=BR⊕BL????????????????????????????? (3)
　　TWO=(~BH)&BR&BL∣ BH&(~BR)&(~BL)
　　= (~BH)&(BR&BL)∣BH&(~(BR∣BL))
　　式中,，BH表示相鄰高位,，BR表示本位，BL表示相鄰低位,。PN為0時為加操作,，為1時為減操作,；ONE為0時操作數為0，為1時操作數為A,；TWO為0時操作數為0,，為1時操作數為2A。
　　如圖1所示,，本乘法器的輸入量為1位符號標志位sign,，用于標識有/無符號數以及16位被乘數A與乘數B。首先根據符號標志位sign將被乘數A與乘數B都轉換為17位的有符號數,。由于布斯編碼需要乘數寬度N為偶數,，故對乘數B再進行1位高位擴展,，因此該乘法器實際操作數變成了17位×18位,。由式(1)可知，對18位的乘數進行改進布斯編碼會產生9(18/2)個部分乘積項,。
2 符號補償技術
　　在乘法器樹型求和過程中,，為了使各個部分乘積項對齊，將需要大量的符號位擴展操作,。因為部分乘積項的符號位可能是1或者0,，所以擴展存在不確定性，直接擴展會造成資源的浪費,。解決的方法是采用符號補償技術^[2],，消除符號位擴展中的不確定性，節(jié)省占用的邏輯資源,，提高運算速度,。
　　符號補償算法描述如下：例如，把8bit有符號數SXXXXXXX擴展為12bit,，其中S表示符號位,，X表示數據位。采用符號位直接擴展時,，可以得到SSSSSXXXXXXX,。對其進行等價邏輯變換：
　　
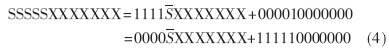
　　于是，符號位擴展轉化成為：對原操作數的符號位取反,，并在高位直接補0,，再對式(4)中第二項的確定部分進行補償。
　　為了簡化電路,，對前面產生的九個PP所需的位擴展進行一次性補償,，補償項就構成第十項部分積，也就是說對每個PP的位擴展都采用符號補償技術,，并把所有的補償項預先加好,，用補償向量V表示,，其求導過程如圖2所示，得到V=11010101010101011,。

3 混合壓縮比樹型結構及乘法器仿真與下載
　　在對部分積求和的過程中,，重復陣列IA結構與Wallace樹結構是兩種典型的壓縮結構。IA結構規(guī)整,，采用串加的形式,，利于產生版圖，但速度較慢,；Wallace樹結構采用并行結構,，可將求和級數從O(N)降為O(log2N)，大幅提高運算速度^[3],，但缺點是布線困難,。兩種結構都不適合實際應用。因此,，大多采用折中的策略^[4～7]把二者結合起來,，使乘法器在速度和占用資源兩方面都有較好的性能，例如ZM樹結構和OS樹結構等,。
　　對于16位×16位有/無符號數乘法器,，由上所述，總共有10個部分乘積項,，需要通過某種樹型結構壓縮為兩項,，即需要一個10-2壓縮器，再通過超前進位加法器得到最終乘積結果,。IA陣列的結構如圖3所示,，Wallace樹結構如圖4所示。在比較各種樹型結構的基礎上,，本文提出了一種適合于16×16有/無符號數乘法器的改進樹型結構,，即混合壓縮比結構，如圖5所示,。

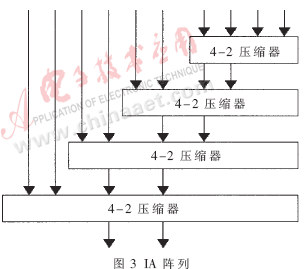
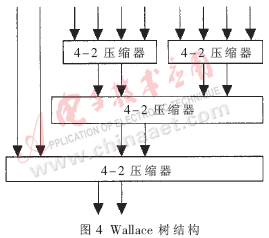
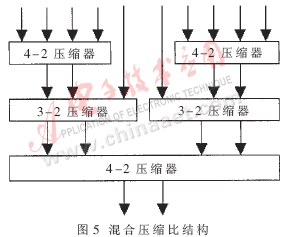
　　各圖中的4-2壓縮器,，也稱為5-3加法器，功能是將四個輸入量壓縮為兩個輸出量,。其代數運算式為：D +C×2+C_o×2=I₀+I₁+I₂+I₃+C_i,。在本設計中采用的輸入輸出邏輯關系如下：
　　
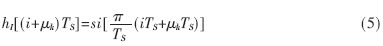
　　混合壓縮比結構中的3-2壓縮器也稱為保留進位加法器(CSA)，其功能是將三個輸入量壓縮為兩個輸出量,。3-2壓縮器的輸入輸出邏輯關系為：
　　
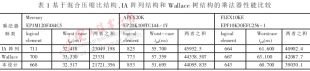
　　分別按照圖3～圖5的樹型結構設計出對應的乘法器,，再對這三種乘法器的性能進行比較。由于構成乘法器的其它模塊相同，所以整個乘法器占用資源多少與延遲大小的區(qū)別完全取決于各自所采用樹型結構的性能優(yōu)劣情況,。
　　在QuartusII環(huán)境中分別對這三種乘法器進行系統(tǒng)級的仿真比較,，結果列于表1中。其中,，logical element參數反映所設計乘法器占用的資源,，Worst-case tpd參數反映乘法器的速度性能，兩者之積可以反映乘法器的綜合性能,。從仿真結果可以看出,，采用Mercury EP1M120F484C5與FLEX10KE EPF10K30EFC256-1芯片，混合壓縮比結構乘法器占用資源與速度的性能都優(yōu)于IA乘法器和Wallace樹乘法器,；而采用APEX20K EP20K100TC144-1V芯片,，混合壓縮比結構乘法器雖然占用資源較多，但是速度最快,，資源與延遲二者之積仍為最小,。因此可以得出結論：本文提出的混合壓縮比結構適合于16×16有／無符號數乘法器，優(yōu)于IA結構和Wallace樹結構,。

　　基于混合壓縮比結構的乘法器時序仿真如圖6所示,，時序仿真采用的芯片為主流系列的FLEX10KE EPF10K30EFC256-1。圖6中所舉算例為：無符號數BCD8×F794,；有符號數FFFF×FFFF；無符號數A7FA×FF9C,；有符號數FF00×7FFF,。仿真結果驗證了乘法器運算正確。需要指出的是,，本乘法器移植在具體系統(tǒng)或者集成芯片時,，其延遲將小于表中的Worst-case tpd數值。
　　最后將所設計的乘法器下載到智能型可編程數字開發(fā)系統(tǒng)CIC-310中,，如圖7所示,。通過大量有/無符號數算例乘法進行硬件驗證，表明該乘法器設計正確,，性能驗證與軟件仿真相符,，可用作數字系統(tǒng)中的乘法器運算單元。

?

　　本文提出了一種適合16×16乘法器的混合壓縮比結構,，其性能優(yōu)于IA結構和Wallace結構,。基于該結構所設計出的乘法器通過了軟件仿真和硬件驗證,，可以作為單元模塊移植在具體系統(tǒng)或者集成芯片中,。所提出的混合壓縮比結構還可以作為10-2壓縮器應用于更高位數乘法器的設計中，具有較強的實用價值,。
參考文獻
1 Booth A D. A Signed Binary Multiplication Technique[J]．Quarterly Journal of Mechanics and Applied Mathematics, 1951,；4(2)：236～240
2 Kwentus A Y,，Hung H T，Wilson AN,，et A1．An Architecture for High-performance/small-area Multipliers for Use in Digital filtering Applications[J]. IEEE J Sol Sta Circ,1994;29(2)：117～121
3 Wallace C S. A Suggestion for a Fast Multiplier[J]．IEEE Transactions on Electronic Computers, 1964,；13(2):14～17
4 許 琪，原 巍,，沈緒榜.一種新的樹型乘法器的設計［J］．西安電子科技大學學報(自然科學版),，2002;29(5)：580～583
5 Wen-Chang Yeh, Chein-Wei Jen. High-speed Booth En-coded Parallel Multiplier Design[J]. IEEE Transactions on Computers, 2000;49(7):692～701
6 K.H.Cheng et al. The Improvement of Conditional Sum Adder for Low Power Applications. Proc,11th,Ann.IEEE Int’l ASIC Conf.1998;131～134
7 Fadavi-Ardekani J.M×N Booth Encoded Multiplier Generator Using Optimized Wallace Trees, Very Large Scale Integration (VLSI) Systems. IEEE Transactions on, 1993;1(2):120～125