現(xiàn)代飛機(jī)上各種用電設(shè)備日益增多,，用電量不斷增加，對(duì)機(jī)載電源的容量,、供電質(zhì)量和可靠性都提出嚴(yán)格的要求,。隨著先進(jìn)技術(shù)在飛機(jī)上的不斷應(yīng)用，對(duì)飛機(jī)供電系統(tǒng)可靠性的要求越來(lái)越高,。飛機(jī)配電系統(tǒng)是供電系統(tǒng)的重要組成部分,，因此研究配電系統(tǒng)的可靠性具有重要意義。現(xiàn)有的可靠性分析方法有最小路法,、最小割集法,、故障樹(shù)分析法、故障模式后果分析法等,。雖然這些可靠性分析方法能比較有效地計(jì)算配電系統(tǒng)的可靠性指標(biāo),，但是實(shí)際運(yùn)用中，對(duì)于大型復(fù)雜系統(tǒng)的定性分析過(guò)程中,，計(jì)算量非常大,，甚至?xí)纬蒒P困難問(wèn)題。
Petri是一種系統(tǒng)描述,、模擬的數(shù)學(xué)和圖形分析工具,，可以表達(dá)系統(tǒng)的靜態(tài)結(jié)構(gòu)和動(dòng)態(tài)變化。因此,，本文提出一種基于Petri網(wǎng)的飛機(jī)配電系統(tǒng)可靠性分析方法,。
1 Petri網(wǎng)概述
Petri網(wǎng)作為一種特殊的有向網(wǎng)，以庫(kù)所和變遷為節(jié)點(diǎn),，有向弧的指示方向表達(dá)系統(tǒng)故障的傳播關(guān)系,。系統(tǒng)的狀態(tài)用庫(kù)所(place)表示，改變狀態(tài)的事件用變遷(transaction)表示,。在Petri網(wǎng)圖形描述中使用“○”代表庫(kù)所,，使用“|”代表變遷，使用有向弧“→”表示序偶,，并由此構(gòu)成Petri網(wǎng)的圖形表示,。如果一個(gè)Petri網(wǎng)的所有有向弧的權(quán)值均為1，則這個(gè)網(wǎng)稱(chēng)為規(guī)范網(wǎng),。這里只考慮規(guī)范網(wǎng)的情況,。
六元組N=(P,，T，I,，O,，M，Mo)若滿足以下條件,，則稱(chēng)為Petri網(wǎng),。
1)P={P1，P2…,，Pn}是庫(kù)所的有限集合,，n為庫(kù)所的個(gè)數(shù)，n>0,；
2)T={T1,，T2…,，Tm}是變遷的有限集合,，m為變遷的個(gè)數(shù)，m>0,，P∩T=空集,；
3)I：PxT→N是輸入函數(shù)，它定義了從P到T的有向弧重復(fù)數(shù)或權(quán)(weight)的集合,，這里N={0,，1…}為非負(fù)整數(shù)集；
4)I：TxP→N是輸入函數(shù),，它定義了從T到P的有向弧重復(fù)數(shù)或權(quán)(weight)的集合,；
5)M：P→N是各庫(kù)所中的標(biāo)識(shí)分布；
6)MO：P→N是各庫(kù)所中的初始標(biāo)識(shí)分布,。
應(yīng)用Petri網(wǎng)分析系統(tǒng)故障,，是將系統(tǒng)所不希望發(fā)生的事件作為頂庫(kù)所，逐級(jí)找出導(dǎo)致這一事件發(fā)生的所有可能因素作為中間庫(kù)所和底庫(kù)所,。用Petri網(wǎng)的基本元素-庫(kù)所和變遷的不同連接可以表示故障樹(shù)模型的邏輯關(guān)系,，可以充分利用圖論的方法來(lái)解決故障模型的診斷推理問(wèn)題。將故障樹(shù)中的頂事件,、中間事件,、底事件用Petri網(wǎng)中的庫(kù)所、變遷,、弧表示,，如圖1所示。
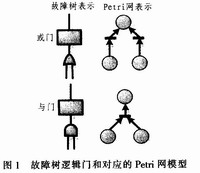
2 基于Petri網(wǎng)的可靠性分析
2．1 定性分析
Petri網(wǎng)模型將故障樹(shù)的各種邏輯連接關(guān)系簡(jiǎn)化為只由庫(kù)所和變遷組成,，以有向弧為連接邊的網(wǎng)絡(luò),，使得系統(tǒng)的故障模型簡(jiǎn)潔,、易懂，故障的傳播關(guān)系一目了然,。目前很多學(xué)者已提出了許多應(yīng)用Petri網(wǎng)求最小割集的方法,，諸如路徑搜索法和庫(kù)所矩陣法等。本文主要介紹一種應(yīng)用Petri網(wǎng)的關(guān)聯(lián)矩陣求最小割集的新算法,，此算法按照指定關(guān)聯(lián)矩陣中所表達(dá)的輸入,、輸出關(guān)系直接從關(guān)聯(lián)矩陣得出割集，易于計(jì)算機(jī)程序的實(shí)現(xiàn),，而且對(duì)于求有重復(fù)事件Petri網(wǎng)模型的割集更為簡(jiǎn)單,、直觀。
Petri網(wǎng)的結(jié)構(gòu)可以用一個(gè)矩陣表示,。若從庫(kù)所P到t的輸入函數(shù)取值為非負(fù)整數(shù)w,，記為I(P，t)=w,，則用從P到t的一有向弧并旁注w表示,；若從庫(kù)所t到P的輸出函數(shù)取值為非負(fù)整數(shù)w，記為O(P,，t)=w,，則用從t到P的的一有向弧并旁注w表示。特別地,，若w=1,，則不必標(biāo)注；若I(P,，t)=0或O(P,，t)=0，則不必畫(huà)弧,。I與O均可表示為nxm非負(fù)整數(shù)矩陣,，O與I之差A(yù)=O-I稱(chēng)為關(guān)聯(lián)矩陣。對(duì)于規(guī)范網(wǎng),，w=1,。下面舉一實(shí)例介紹關(guān)聯(lián)矩陣求最小割集的方法步驟。
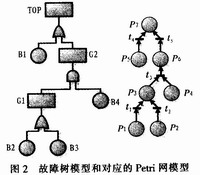
由圖2中Petri網(wǎng)模型求其關(guān)聯(lián)矩陣：
可以看出,，在此關(guān)聯(lián)矩陣中,，-1表示有向弧由庫(kù)所指向變遷，此庫(kù)所為變遷的輸入庫(kù)所,；1表示有向弧由變遷指向庫(kù)所,，此庫(kù)所是變遷的輸出庫(kù)所。根據(jù)上述關(guān)聯(lián)矩陣得出求Petri網(wǎng)的最小割集的步驟如下：
1)找出關(guān)聯(lián)矩陣中只有1和0,，沒(méi)有-1的行,，則該行對(duì)應(yīng)為頂庫(kù)所(只有輸入庫(kù)所,，沒(méi)有輸出庫(kù)所)，由此庫(kù)所開(kāi)始尋找(在此關(guān)聯(lián)矩陣中為最后一行),。
2)由頂庫(kù)所對(duì)應(yīng)的行的1出發(fā)按列尋找-1,，此-1所對(duì)應(yīng)行代表的庫(kù)所為頂庫(kù)所的一個(gè)輸入庫(kù)所，如果該列有多個(gè)-1,，則說(shuō)明對(duì)應(yīng)同一變遷有多個(gè)輸入庫(kù)所,，并且輸入的庫(kù)所為“相與”關(guān)系。
3)由步驟2)找到的-l按行尋找1,，如果有1說(shuō)明該庫(kù)所為中間庫(kù)所,，則按步驟2)循環(huán)查找，直到所在行沒(méi)有1為止,；如果沒(méi)有1,，則說(shuō)明該庫(kù)所是一個(gè)底庫(kù)所；如果該行有多個(gè)1,，則說(shuō)明由這些1對(duì)應(yīng)的庫(kù)所應(yīng)為“相或”關(guān)系,。
4)按步驟2)和步驟3)繼續(xù)查找，直到查找到最底庫(kù)所為止,。
5)按照前面的“相與”,、“相或”關(guān)系將底庫(kù)所展開(kāi),，則得到所有割集,。
6)按照布爾吸收律或素?cái)?shù)法得到最小割集。
按照上述步驟可寫(xiě)出：
P7=P6+P5=P3xP4+P5=(P1+P2)×P4+P5=P1×P4+P2×P4+P5
可知最小割集為{P1,，P4},，{P2，P4},，{P5},。
2．2 定量計(jì)算
在得到故障樹(shù)的全部最小割集后，可通過(guò)最小割集來(lái)求頂事件發(fā)生的概率,。設(shè)頂事件發(fā)生的概率為P(T),，C1={P1，P4},，C2={P2,，P4}，C3={P5},。則：
3 基于Petri網(wǎng)的飛機(jī)配電系統(tǒng)可靠性分析
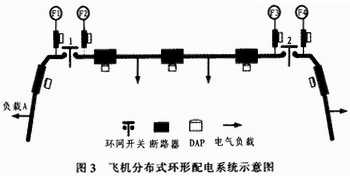
圖3是一個(gè)簡(jiǎn)化的飛機(jī)分布式環(huán)形配電系統(tǒng)部分示意圖,，它采用配電線路無(wú)通道自動(dòng)繼電保護(hù)技術(shù)控制斷路器和環(huán)網(wǎng)開(kāi)關(guān)的通斷，從而達(dá)到故障隔離和容錯(cuò)供電的目的,。
3．1 建立故障樹(shù)
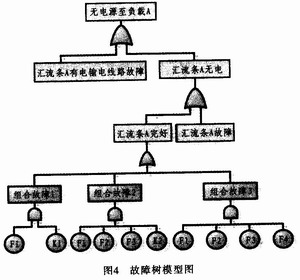
圖4為故障樹(shù)模型圖,。圖中,，F(xiàn)n代表n號(hào)發(fā)電機(jī)故障，Kn代表n號(hào)環(huán)網(wǎng)開(kāi)關(guān)故障,。
3．2 將故障樹(shù)模型轉(zhuǎn)化為Petri網(wǎng)模型
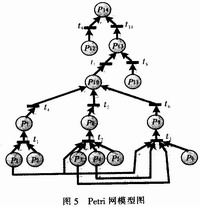
圖5為Petri網(wǎng)模型圖,，Pn分別代表圖4故障樹(shù)中對(duì)應(yīng)的事件。
3．3 應(yīng)用Petri網(wǎng)的關(guān)聯(lián)矩陣求最小割集
按照上述求最小割集的步驟可以得出：
P14=P13+P12=P10+P11+P12=P7+P8+P9+P11+P12=P1P2+P1P3P4P5+P1P3P4P6+P11+P12
從而得到其最小割集：C1={P1,，P2},，C2={P1，P3,，P4,，P5}，C3={P1,，P3,，P4，P6},，C4={P12},。C5={P12}。同樣,，再利用上述定量計(jì)算的方法即可得出頂事件發(fā)生的概率,。
4 結(jié)束語(yǔ)
飛機(jī)配電系統(tǒng)可靠性分析中經(jīng)常使用故障樹(shù)分析法，雖然較好地解決了配電系統(tǒng)的可靠性分析問(wèn)題,，但是實(shí)際應(yīng)用中表現(xiàn)出分析復(fù)雜和計(jì)算量大的缺點(diǎn),，不利于對(duì)配電系統(tǒng)進(jìn)行快速有效的評(píng)估。將故障樹(shù)模型轉(zhuǎn)化為Petri網(wǎng)模型進(jìn)行分析計(jì)算,，可以極大地簡(jiǎn)化故障樹(shù)分析中的計(jì)算,，彌補(bǔ)了傳統(tǒng)故障樹(shù)分析法的不足。