1引言

　　變壓器通常有電源變壓器和信號變壓器兩大類,。

　　磁性元件是電源開關(guān)變換器和信號變壓器中的必備元件,。由于磁材料特性的非線性,，其特性對溫度,、頻率,、氣隙的依賴性使得磁材料參數(shù)測量較為困難,，因此在進行磁元件設(shè)計時,，需要對磁元件的參數(shù),、一般特性和設(shè)計方法有一定的了解。首先,，本文的主要部分敘述變壓器磁學(xué)的基本理論和磁學(xué)定理,、參數(shù)的含義和解釋。其次,，敘及變壓器的性能模型和等效電路,，對變壓器的各種參數(shù)和術(shù)語進行解釋。還對設(shè)計高頻開關(guān)電源時遇到的高頻電流效應(yīng)問題作一簡介,，最后對變壓器測試時所用到的變壓器等效電路參數(shù)的測量方法作一些敘述,。

　　為了領(lǐng)會實際變壓器在應(yīng)用時的性能，在純電阻負載的情況下,，用變壓器寬帶信號的頻域響應(yīng)特性,，推導(dǎo)出實用的一般等效電路模型。

　　時域響應(yīng)特性曲線最能說明等效電路參數(shù)對加在其上脈沖波形的上升沿,、峰值和下降沿的影響,。對采用高重復(fù)率數(shù)字脈沖信號的局域網(wǎng)（LAN）和長途通信來說，變壓器對這種脈沖信號的響應(yīng)是應(yīng)特別重視的,。

2變壓器磁學(xué)的基本原理

2.1法拉弟定律

　　電和磁相互之間有著緊密的聯(lián)系,。磁場是電荷（電流）運動的結(jié)果,。反之，如果把一根導(dǎo)體放在隨時間變化的磁場里,，在導(dǎo)體上就會產(chǎn)生感應(yīng)電動勢(emf),。法拉弟定律指出這個感應(yīng)電動勢是和磁通量的變化率成正比的。

e=－dψ/dt=－NdΦ/dt(1)

式中e—感應(yīng)電動勢（單位：V）

N—繞組匝數(shù)

t—時間（單位：s）

Φ—磁通量（單位：Wb）

ψ—磁鏈（單位：Wb）

　　理想變壓器就是按照法拉弟定律把加在輸入繞組的電能通過磁場傳遞給輸出繞組,。

2.2理想變壓器

　　原邊和副邊繞阻的匝比為1:n的簡化變壓器如圖1所示,。

圖1理想變壓器

　　在變壓器原邊加一隨時間變化的電壓u1，它會產(chǎn)生一個流過原邊繞組的電流i1,。這個電流就會在磁心中產(chǎn)生一個磁通Φ,，假設(shè)Φ全部通過磁心并全部通過副邊繞組。則磁心中的磁通Φ就會在變壓器副邊繞組感應(yīng)出一個電壓u2和電流i2,。

　　上述關(guān)系可用式（1）表示為：

u1=－N1dΦ/dt和u2=－N2dΦ/dt(2)

因此U1/U2=N1/N2=1/n

2.3磁通密度

　　在圖1所示的理想變壓器中,，磁通Φ全部通過

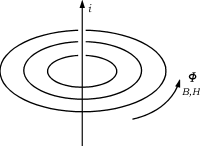
圖2電流與磁場

磁心，如磁心的橫截面積為A,，則磁心內(nèi)部的磁通密度定義為：

B=Φ/A(Wb/m2)(3)

2.4磁場強度

　　安培定律指出：(A)（4）

即在一個閉合磁路中,，各段磁通路徑長度li和相應(yīng)磁場強度Hi乘積的總和等于施加的安匝數(shù)NI。

　　對于一個理想的磁路,，即磁路中各點的磁場強度是一常數(shù)時，則NI=Hl,，因此

H=NI/l(A/m)(5)

2.5材料的磁導(dǎo)率

　　磁感應(yīng)強度（B）是磁場強度（H）的函數(shù),。它們之間的關(guān)系是：

B=μH（6）

式中μ—磁導(dǎo)率（單位：H/m）

　　B—磁感應(yīng)強度（單位：T）

　　H—磁場強度（單位：A/m）

在空氣隙中的磁導(dǎo)率μ是一常數(shù)（μ=μO=4π×10－7

H/m）。其它材料B－H關(guān)系曲線的一般形式如圖3所示,。初始磁導(dǎo)率μi[1]是磁性材料磁化曲線始端磁導(dǎo)率的極限值,，即：2.6B－H曲線

圖3B－H曲線

　　圖3展示的B－H曲線是一磁滯回線[2]，在B和H的增量很小范圍內(nèi),，磁導(dǎo)率μ可以認為是一常數(shù),。

　　如果導(dǎo)磁材料曲線起始部分磁場強度H值增加，則對應(yīng)的B值就沿著曲線1→曲線2增加,。在B和H是零的那一點曲線的斜率稱為初始磁導(dǎo)率,。當(dāng)H值增加,到達點2以后，B值就不再隨之增加,。稱此點為飽和點,它對應(yīng)的B=BS,。此時如減小H值，B和H關(guān)系曲線的軌跡變?yōu)?→3→4,。當(dāng)H減小到零時（2與3點之間）,，B有一剩余值，B=Br,。當(dāng)H反向后,，B又逐漸減小,，在點3，B值再次等于零,，此時稱為矯頑力,H=HC,。反向H作用下的點4也是飽和點。如果此時H增加,，對應(yīng)曲線的軌跡是4→5→2,。此時曲線不再通過1點。

　　在純交流電的狀態(tài)下,，B－H曲線每一周期的軌跡都是2→3→4→5→2的環(huán)狀曲線,。

　　B－H曲線的磁滯回線與磁心損耗有聯(lián)系，磁心損耗與磁滯回線環(huán)的面積成正比,。

2.7相對磁導(dǎo)率

　　磁性材料的相對磁導(dǎo)率定義如下：

μr=μ/μo(7)

式中μr—材料的相對磁導(dǎo)率

μ—材料的絕對磁導(dǎo)率

μ0—真空磁導(dǎo)率[3]

2.8磁阻

根據(jù)圖1理想變壓器,，應(yīng)用式（4）可寫出：

Ni=N1i1－N2i2和∑Hili=Hl=Bl/μ=lΦ/Aμ

磁阻Rm=l/Aμ(H－1)(8)

N1i1=ΦRm＋N2i2(9)

式（9）等式右邊表示輸出可得到的有效安匝數(shù)，要比等式左邊的輸入安匝數(shù)小ΦRm,，這一項相當(dāng)于在磁心內(nèi)部建立起磁場所需的磁勢,，稱它為磁心的勵磁。

　　在理想情況下,，當(dāng)μ→∞Rm→0,，則

i1/i2=N2/N1=n(10)

2.9自感

　　線圈的自感是線圈電流所產(chǎn)生的磁場在線圈上所形成的電感。它的定義如下：

e=－Ldi/dt(11)

式中L—自感（單位：H）

　　e—電感上電壓（單位：V）

　　t—時間（單位：s）

各種幾何形狀電感的計算中,，如包含有和安掊定律有關(guān)的H及I的求和/求積計算時,，要求出它的電感量是比較復(fù)雜的。舉一簡單實例,，求一環(huán)形磁心上理想

線圈的電感（見圖4）,。

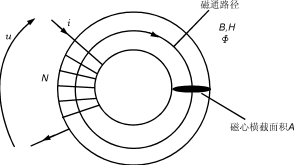
圖4環(huán)形磁心上的電感

　　從法拉弟定律可得：

u=NdΦ/dt=NAdB/dt，于是

u=NAμdH/dt(12)

　　從安培定律可得：

　　Ni=Hl（13）

由式（12）和（13）可得：　　于是可求出電感為：

L=N2Aμ/l(14)

2.10互感

　　對于變壓器和其它耦合線圈還應(yīng)考慮副邊（和其它）線圈對原邊線圈所產(chǎn)生磁場的影響,。兩個線圈之間耦合磁通的影響所導(dǎo)致的電感稱之為互感,。

　　我們考慮兩個線圈在同一個磁心上的情況。在一般情況下,，不是所有磁通和所有線圈都耦合,，如圖5所示。

圖5耦合線圈

　　按照安培定律可以寫出：

Φ12=a(N1i1＋N2i2)

Φ11=bN1i1

Φ22=cN2i2

式中a,、b和c表示有效的比例常數(shù),。

　　按照法拉弟定律可以寫出：

u1=N1d(Φ11＋Φ12)/dt

u2=N2d(Φ22＋Φ12)/dtu1=N12(a＋b)＋N1N2au2=N22(a＋c)＋N1N2a

又可以寫出：

L1=N12（a＋b）—線圈1的自感

L2=N22(a＋c)—線圈2的自感

M=N1N2a—兩個線圈之間的互感

　　在完全耦合的情況下Φ11=0、Φ22=0和b=0,、c=0,。因此，對于完全耦合的線圈可以認為：(15)

2.11耦合系數(shù)

　　耦合線圈在實際情況下,，不是所有磁通都從耦合繞組的中間穿過,。在2.10節(jié)中的常數(shù)b和c不再為零,。表示線圈磁通耦合情況的另一種方法是用線圈的耦合系數(shù)k：M=k(16)

式中0≤k≤1

2.12同名端

　　簡單變壓器常規(guī)電路的同名端符號如圖6所示。

　　每一繞組上方打的點是用來表示電感的同名端和繞組感應(yīng)電動勢的相位,。當(dāng)同名端和電流,、電壓的常規(guī)方向如圖6所示時，則變壓器的方程可寫成下列形式：

u1=L1di/dt＋Mdi2/dt

u2=L2di2/dt＋Mdi1/dt

圖6變壓器電路的同名端

　　如果電壓或電流的方向和圖上標(biāo)的相反時,，則對

應(yīng)項的符號也必需相反,。

　　在通常的情況下，常規(guī)電壓的方向是朝向“點”的方向,，電流是通過“點”流進繞組,。

2.13阻抗換算

　　當(dāng)涉及變壓器的電路分析時，通常都是把變壓器副邊阻抗換算成接在原邊時的等效阻抗,。這就是通常說的簡化等效電路,。

　　(1)并聯(lián)阻抗換算

　　從視在功率S方面考慮可把阻抗改寫如下：

S2=U22/Z2

從式（2）可得U1=U2/n，因而

S2=U12n2/Z2

所以跨接在變壓器原邊的等效阻抗是：Z1=Z2/n2,，如圖7所示,。

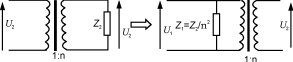
圖7并聯(lián)阻抗換算

　　(2)串聯(lián)阻抗換算

　　從視在功率S方面考慮還可把阻抗改寫如下：

　　S2=I22Z2，從式（10）可得i1=ni2,，因而

S2=I21Z2/n2

　　所以跨接在變壓器原邊的等效阻抗是：Z1=Z2/n2,，如圖8所示。

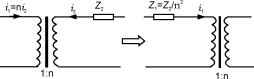
圖8串聯(lián)阻抗換算

2.14磁心氣隙的影響

　　一個具有空氣隙（為了清楚起見,，圖中的氣隙是放大了的）的簡單變壓器的磁心如圖9所示,。磁心的等效磁通路徑的長度是l，空氣隙的長度是lg,。

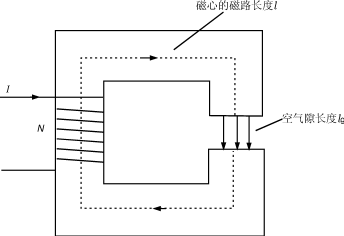
圖9具有空氣隙的磁心

　　假設(shè)氣隙很小，則磁通和氣隙界面垂直（沒有邊緣效應(yīng)）,，并通過氣隙保持連續(xù),，加上磁心材料內(nèi)部的磁感應(yīng)強度和界面是正交的，所以可寫出下式：

B=μ0Hair=μ0μrHcore

所以Hair=μrHcore（17）

式中Hair—空氣隙中的磁場強度

Hcore—磁心中的磁場強度

同樣從安培定律可得：

NI=H×磁路長度,，則

NI=Hairlg＋Hcorel=Hcore(μrlg＋l)

對上式重新排列,，可寫出磁心的磁場強度：

Hcore=NI/l(1＋aμr);（18）

式中a=lg/l(0≤a≤1)

　　式（18）表示有空氣隙磁心內(nèi)部的磁場強度為沒有空氣隙磁心內(nèi)部磁場強度的1/（1＋aμr）（假設(shè)lg和l相比是很小的）。按照這一關(guān)系,，如要求有空氣隙磁心的磁場強度進入飽和區(qū),，則要求加在磁心上的安匝數(shù)增加(1＋aμr)倍。

　　實例：一個具有等效磁路長度為5cm,、相對磁導(dǎo)率為5000,、總的空氣隙長度為0.1mm的鐵氧體磁心在數(shù)值NI左右進入飽和區(qū)。它比等效沒有空氣隙的磁心所要求的安匝數(shù)要高出11倍,。

　　在通信系統(tǒng)中,，當(dāng)有直流電流流過變壓器的繞組時,，為了防止磁心飽和，使用有空氣隙磁心是常見的,。使用大的空氣隙磁心會導(dǎo)致邊緣效應(yīng)加大（因為不是所有磁通都包含在氣隙內(nèi)部）,，它也會使匝間漏電感和雜散電容增大。

　　磁性材料的飽和點μ=0,，考慮到e=－NdΦ/dt=－NAμdH/dt,，所以如μ=0，則e=0,。即變壓器喪失變換的功能,。

　　如同H∝i一樣，一般電感器的電感量∝μ,，因此,，當(dāng)μ=0時，電感等于零,。

　　超出磁心的飽和點以后,，則變壓器喪失它的功能。

3變壓器等效電路

　　研究理想變壓器的假設(shè)條件是：

　?。?）磁心材料有足夠大的磁導(dǎo)率,，其值可等效地看作是無限大(μ∞)；

　?。?）勵磁電流足夠小,，其值可等效地看作是零（im=0）；

　?。?）磁心的任何損耗都小到可以忽略,；

　　（4）線圈繞組的電阻小到可以忽略,；

　?。?）所有繞組之間的磁通都是完全耦合，沒有磁通“泄漏”（k=1）,；

　?。?）繞組間的電容小到可以忽略。

　　但實際變壓器不是這樣的,。下面我們將研究實際變壓器的等效電路,。

3.1有限磁導(dǎo)率

　　如果μ是有限的，則im將不等于零,，在原邊繞組中就有勵磁電流存在,。

　　從式（9）和（10），可寫出：

i1=ΦRm/N1＋N2i2/N1=im＋ni2

式中im是勵磁電流,。這一增加的電流可以在等效電路中增加一個和原邊線圈并聯(lián)的電感Lm來表示,，如圖10所示,。

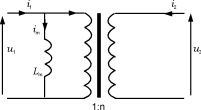
圖10磁心勵磁電流

3.2磁心損耗

　　（1）磁滯損耗

　　在2.6節(jié)已敘述了環(huán)形磁心B－H之間的滯后關(guān)系以及和磁滯回線閉合曲線面積成正比的損耗,。閉合曲線面積和頻率成正比,，在頻率是恒定時（盡管對脈沖變壓器來說，變壓器工作頻率的變化率是一含糊的概念）,，從實驗推導(dǎo)出的磁滯損耗公式是：

Ph=khBmax1.6(W)(19)

式中kh—是材料的磁滯損耗系數(shù),。

　　（2）渦流損耗

　　由法拉弟定律可知,，當(dāng)磁心中磁通交變時,，磁心中亦會產(chǎn)生感應(yīng)電動勢，這個感應(yīng)電動勢會在磁心材料上產(chǎn)生環(huán)形電流,，這個電流會在磁心的有限電阻上引起功率損耗,。這個損耗和頻率的平方成正比，但在頻率基本恒定和磁通近似均勻分布時可得：

Pe=keB2max（W）(20)

式中ke—是材料的渦流損耗系數(shù),。

　?。?）磁心損耗

　　磁滯損耗和渦流損耗兩項合并，就能求得磁心損耗近似值的有用模型,。

Pc=khBmax1.6＋keBmax2≈αΦ2max

式中Φmax和電壓U1max成正比,，所以Pc∝U1max2。雖然這僅僅是一個不嚴密的近似,，但它使我們能用一個并聯(lián)在原邊繞組兩端的等效電阻RC來作為磁心損耗的模型,，如圖11所示。

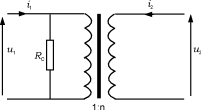
圖11鐵心損耗的等效電阻

　　為了減小磁心損耗,，可用高電阻率的磁性材料（如鐵氧體磁性材料）或用能減少渦流電流的磁心結(jié)構(gòu)（如疊片鐵心）,。

3.3繞組電阻

　　用來繞制變壓器線圈的導(dǎo)線，其電阻不為零,，所以它將在每一繞組上產(chǎn)生電阻損耗,。為此在等效電路中每一線圈上增加一個串聯(lián)電阻，如圖12所示,。

圖12繞組電阻

　　為了減小繞組損耗,，應(yīng)盡量用較大截面積的導(dǎo)線或盡量減少匝數(shù),。

3.4漏磁通

　　在2.10節(jié)已經(jīng)提到磁通不可能完全耦合所有的線圈（即有漏磁通）,，線圈的自感可寫成：

　　L1=N12（a＋b）和L2=N22(a＋c)

　　首先考慮原邊。原邊中的aN12項可認為是忽略漏感的理想自感,，而bN12項相當(dāng)于漏感的作用（即漏電感）,。所以可在等效電路的理想原邊線圈上增加一個串聯(lián)電感來表示漏磁通的影響，如圖13所示,。這種論證同樣適用于同一變壓器的副邊線圈,。

圖13漏感

　　漏電感大小與線圈繞制工藝和磁心幾何結(jié)構(gòu)有關(guān),。

3.5分布電容

　　在實際變壓器的繞組中存在寄生電容。最值得注意的是線圈導(dǎo)線和變壓器磁心之間以及各繞組之間的寄生電容,。電容量的大小由繞組的幾何形狀,、磁心材料的介電常數(shù)和它的封裝材料等來決定（如在設(shè)備中可用環(huán)氧樹脂密封封裝或繞組內(nèi)部用聚四氟乙烯絕緣）。原,、副邊電容效應(yīng)是由線圈匝間的電容引起的,，盡管匝和匝之間的電容通常是很小的，因電容串聯(lián)之和要比并聯(lián)的小,，但作為一個繞組間分布電容的模型,，也應(yīng)在變壓器等效電路每一理想線圈兩端并聯(lián)一個集中的電容，如圖14所示,。

圖14分布電容

　

3.6繞組之間的電容

　　在變壓器原邊和副邊繞組之間的電容（圖15中的CWW）,。這個電容的大小取決于繞組的幾何形狀、變壓器磁心材料的介電常數(shù)和它的封裝材料等,。通常這個電容和變壓器的電感相比是很小的,，它的影響只有在工作頻率高于變壓器的上限截止頻率時才起作用。

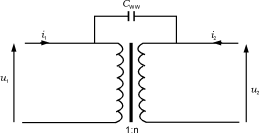
圖15繞組之間的電容

3.7綜合等效電路

　　綜合3.1～3.6節(jié)所述的非理想因素,，可以得出變壓器的一般等效電路,如圖16所示,。

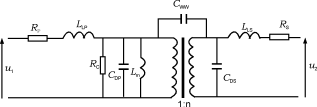
圖16變壓器的一般等效電路