李百華1,，郭燦彬1,鐘其水2,，涂濤2

　　（1.廣東機(jī)電職業(yè)技術(shù)學(xué)院,，廣東 廣州 510515,；2.電子科技大學(xué) 航空航天學(xué)院，四川 成都 611731）

       摘要：首先分析了鋰離子電池的特性和充放電原理，介紹了鋰離子電池的戴維南（Thevinin）等效電路模型,，并采用脈沖法和遞推最小二乘法相結(jié)合對戴維南等效電路模型參數(shù)進(jìn)行辨識,，實(shí)現(xiàn)了戴維南等效電路模型參數(shù)的實(shí)時在線辨識，為電動汽車鋰電池的等效電路模型的分析研究提供了一種可行方式,。

　　關(guān)鍵詞：電動汽車,；等效電路；脈沖法,；最小二乘法

　　中圖分類號：U469.72+2文獻(xiàn)標(biāo)識碼：ADOI： 10.19358/j.issn.1674-7720.2017.01.025

　　引用格式：李百華,，郭燦彬，鐘其水,，等. 電動汽車鋰電池戴維南等效電路模型參數(shù)辨識研究［J］.微型機(jī)與應(yīng)用,，2017,36（1）：83-85，88.

0引言

　　隨著汽車需求不斷上升,，能源短缺與環(huán)境污染日趨嚴(yán)重,，電動汽車具有無污染、電能來源多樣的優(yōu)點(diǎn),，其發(fā)展得到廣泛重視,。電動汽車鋰電池存在過充或過放后將產(chǎn)生不可恢復(fù)的破壞性影響，不正常工作狀態(tài)下將會導(dǎo)致自燃等安全問題［1］,。通過建立有效理論模型對其工作狀態(tài),、特性和性能作有效評價是必要的。

　　目前,，常用的電池模型有多種,，戴維南等效電路模型由于模型參數(shù)簡單、計(jì)算量適中得到廣泛采用,。本文通過分析戴維南等效電路模型,，研究等效電路模型參數(shù)辨識，得到該等效電路模型參數(shù)的確定方法［2］,。

1鋰離子電池充放電原理

　　鋰離子電池正極一般采用鈷酸鋰,、錳酸鋰、磷酸鐵鋰,、鎳酸鋰等鋰離子化合物,，負(fù)極一般采用石墨等可以嵌入鋰離子的化合物［3］。磷酸鐵鋰離子電池正極充放電變化如圖1所示,，鋰離子通過電解液和電池隔膜在電池的正負(fù)極間來回轉(zhuǎn)移,。

2戴維南（Thevinin）等效電路模型

　　電池組等效為電壓源、內(nèi)阻,、一階RC串聯(lián)的電路,，如圖2所示,，其中R1是電池的歐姆內(nèi)阻，一階RC表征電池充放電過程中極板的極化電容和電阻［4］,。這樣電池組充放電過程中電壓的突變特性可由內(nèi)阻R1表征,，電壓的漸變特性可由Rp和Cp表征。

　　戴維南模型中,，歐姆內(nèi)阻R1由電池電解質(zhì),、正極鋁箔、負(fù)極銅箔等組成,，用一階的RC串聯(lián)電路反應(yīng)電池充放電時電壓的漸變特性,，一階RC電路由電池充放電過程中正極和負(fù)極的極化效應(yīng)產(chǎn)生。

3戴維南等效電路模型參數(shù)辨識

　　3.1遞推最小二乘法

　　對于多元線性方程,，在未知數(shù)個數(shù)小于方程個數(shù),，方程無解的情況下［5］，可以通過最小二乘法計(jì)算方程的最小二乘解,。M抽頭濾波器的權(quán)向量應(yīng)滿足的線性方程如式(1)所示,。

　　Aw=b(1)

　　式中A是列滿秩矩陣，且A的行數(shù)大于列數(shù),，即式(1)中,，獨(dú)立方程數(shù)大于未知數(shù)的數(shù)目，因此方程無解,。但是,，應(yīng)用最小二乘法可以計(jì)算方程的一個近似解，通過取得極小值并求導(dǎo)后可以得到式(2)：

　　LS=(AHA)－1AHb(2)

　　式(2)即為方程的最小二乘解,。將最小二乘解推廣到遞推最小二乘(RLS)解需要假定系數(shù)矩陣A如式(3)所示。

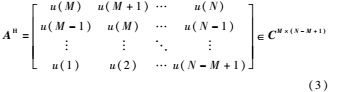
　　其中M為濾波器系數(shù)的個數(shù)或者線性方程的未知數(shù)個數(shù),，N－M+1為觀測數(shù)據(jù)的個數(shù),，或者線性方程的個數(shù)。為了充分利用觀測數(shù)據(jù),，可以將矩陣A擴(kuò)展為式(4)所示的結(jié)果,。

　　式(1)中相關(guān)矩陣如式(5)所示:

　　3.2復(fù)頻域分析

　　鋰電池的戴維南模型等效電路如圖2所示，將該模型的電路數(shù)學(xué)方程轉(zhuǎn)換到復(fù)頻域可得電路輸出方程如下所示:

　　式(9)中,，U(s)為電池端電壓復(fù)頻域值,，I(s)為電流復(fù)頻域值，R1為電池內(nèi)阻值,，Rp和Cp為電池極化電阻和極化電容,。同時得到電池阻抗如下所示:

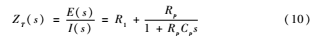
　　式(10)中， E(s)=Uoc(s)－U(s),，根據(jù)雙線性變換原理可得:

　　將式(11)帶入式(10)可得z域下鋰電池戴維南模型參數(shù)表達(dá)式如下所示:

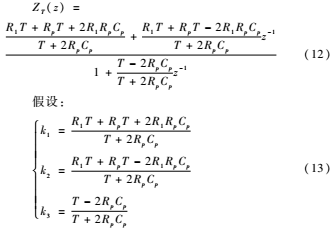
　　從而可得：

　　E(k)=k1I(k)+k2I(k－1)+k3E(k－1)(14)

　　3.3脈沖放電實(shí)驗(yàn)和遞推最小二乘法結(jié)合辨識戴維南模型參數(shù)

　　由式(13)可知,，參數(shù)k3只與采樣周期和時間常數(shù)有關(guān),，時間常數(shù)可由脈沖放電實(shí)驗(yàn)獲得，脈沖放電實(shí)驗(yàn)的系統(tǒng)如圖3所示,。

　　圖4是磷酸鐵鋰電池以10 A電流放電的端電壓變化曲線,。

　　圖4中電池端電壓的漸變過程是由電池的極化電阻和極化電容引起的，通過MATLAB進(jìn)行曲線擬合可得電壓漸變段電池端電壓與時間的方程關(guān)系,，如下所示：

　　U=0.051 9exp(-0.092 5t)+3.269 0(15)

　　由式(15)可知,，電壓漸變曲線的時間常數(shù)如下式所示:

　　式(19)中，b(n)=E(n)－0.687 76E(n－1),，φ(n)=［I(n)I(n－1)］,，θ(n)=［k1k2］T。b(k)的值與E(k)相關(guān),，而E(k)的值與電池的開路電壓值Uoc(k)相關(guān),，電池的開路電壓值Uoc(k)可由電池剩余電量SOC(k)求得，因此,，這里需要獲得電池SOC值和開路電壓值Uoc間的擬合曲線,。

　　為了獲取鋰電池SOC值和開路電壓Uoc間的擬合曲線關(guān)系，可以對鋰電池進(jìn)行雙脈沖放電實(shí)驗(yàn),，獲取指定SOC值下的開路電壓值,，從而進(jìn)行擬合［6］。鋰電池雙脈沖放電的端電壓曲線如圖5所示,，實(shí)驗(yàn)中,，充放電脈沖電流大小都是10 A，脈沖寬度為40%,。

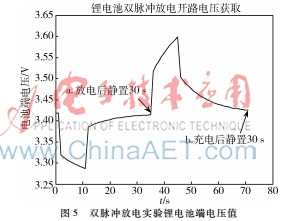
　　圖5中,，a點(diǎn)是電池脈沖放電結(jié)束后，靜置了30 s的端電壓值,，在靜置過程中,，電池極化電壓將逐漸降低，電池端電壓值逐漸趨近電池開路電壓值,。b點(diǎn)是電池充電結(jié)束后,，靜置了30 s的端電壓值，在靜置過程中,，電池充電極化電壓逐漸降低,，電池端電壓值逐漸趨近電池開路電壓值。由于電池脈沖充放電的時間很短,，因此,，電池的SOC可以認(rèn)為不變,a點(diǎn)和b點(diǎn)分別是電池放電后靜置一段時間和充電后靜置一段時間的端電壓值，所以,，電池的開路電壓值一定介于a點(diǎn)和b點(diǎn)電壓值之間,，可以取a,、b點(diǎn)電壓的平均值作為電池的開路電壓值。通過雙脈沖法測得不同SOC值的開路電壓值如表1所示,。

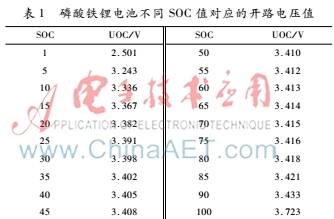
　　根據(jù)表1,，通過分段擬合可得磷酸鐵鋰電池SOC和開路電壓間的擬合曲線如圖6所示。

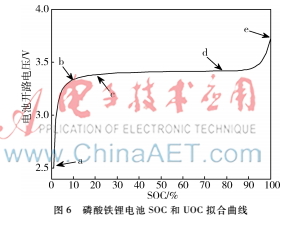
　　圖中a~b段采用5次擬合,，b~c段采用3次擬合,，c~d段采用二次擬合，d~e段采用5次擬合,。通過分段擬合的方式獲取鋰離子電池SOC值和開路電壓值間的曲線關(guān)系,，可以大大提高通過電池SOC值獲取開路電壓值的精度。

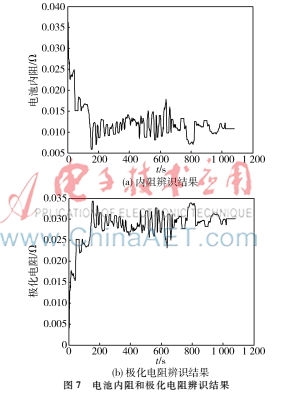
　　電流I(k)可以通過實(shí)驗(yàn)測得,，令λ=1,u(n)=I(n),，帶入式(8),可迭代計(jì)算k1、k2的值,，將k1,、k2的值代入式(17)即可求得R1、Rp的迭代值,。通過實(shí)驗(yàn)得到R1,、Rp的估算值如圖7所示。

4結(jié)論

　　本文首先分析了鋰離子電池的特性和充放電原理,，介紹了鋰離子電池戴維南等效電路模型,，并采用脈沖法和遞推最小二乘法相結(jié)合對戴維南等效電路模型參數(shù)進(jìn)行辨識。通過雙脈沖法測得了不同SOC值下磷酸鐵鋰電池的開路電壓值,，并對磷酸鐵鋰電池的SOC和開路電壓值進(jìn)行了分段擬合,。通過脈沖放電法和遞推最小二乘法實(shí)現(xiàn)了戴維南等效電路模型參數(shù)的實(shí)時在線辨識。該方法為電動汽車鋰電池的等效電路模型的分析研究提供了一種可行方式,。

參考文獻(xiàn)

　?。?］ 張禹軒. 電動汽車動力電池模型參數(shù)在線辨識及 SOC 估計(jì)［D］.長春：吉林大學(xué)，2014.

　?。?］ 周美蘭, 趙強(qiáng), 周永勤. 改進(jìn)的PSOBP神經(jīng)網(wǎng)絡(luò)估算磷酸鐵鋰電池SOC［J］. 哈爾濱理工大學(xué)學(xué)報(bào), 2015, 20(4):88-92.

　?。?］ GREGORY L P. LiPB dynamic cell models for Kalmanfilter SOC estimation［A］. Proceedings of the 19th International Electric Vehicle Symposium［C］. Busan:EVS,2002：1860-1871.

　?。?］ 張東華,馬燕,，陳思琪，等.鋰電池模型參數(shù)估計(jì)與荷電狀態(tài)估算研究［J］.武漢理工大學(xué)學(xué)報(bào),2015,37(2):179-182.

　?。?］ 范興明, 曾求勇,張鑫. 基于改進(jìn)安時積分法的電動汽車電池SOC估計(jì)與仿真研究［J］.電氣應(yīng)用, 2015(8):111-115.

　?。?］ Shang Yunlong, Zhang Chenghui, Cui Naxin, et al. A celltocell battery equalizer with zerocurrentswitching and zerovoltage gap based on quasiresonant LC converter and boost converter［C］. IEEE Transactions on Power Electronics, 2015, 30(7):3731-3747.