1引言![]()
![]()
![]() 對(duì)于SPWM三相半橋式逆變器,由于開(kāi)關(guān)管固有開(kāi)關(guān)時(shí)間ts的影響,開(kāi)通時(shí)間ton往往小于關(guān)斷時(shí)間toff,因此容易發(fā)生同臂兩只開(kāi)關(guān)管同時(shí)導(dǎo)通的短路故障。為了避免這種故障的發(fā)生,通常要設(shè)置開(kāi)關(guān)死區(qū)△t,以保證同橋臂上的一只開(kāi)關(guān)管可靠關(guān)斷后,另一只開(kāi)關(guān)管才能開(kāi)通。死區(qū)的設(shè)置方式有兩種:一種是提前關(guān)斷、延滯開(kāi)通的雙邊對(duì)稱(chēng)設(shè)置;另一種是按時(shí)關(guān)斷、延滯△t開(kāi)通的單邊不對(duì)稱(chēng)設(shè)置。典型的電壓型三相SPWM半橋式逆變器如圖1(a)所示。其中圖1(b)是死區(qū)對(duì)稱(chēng)設(shè)置時(shí)的波形圖;圖1(c)是死區(qū)不對(duì)稱(chēng)設(shè)置時(shí)的波形圖。在這兩種波形圖中,uAO為相與直流電源中點(diǎn)“0”之間的理想電壓波形(載波比),uAO′為設(shè)置死區(qū)時(shí)的電壓波形。
對(duì)于SPWM三相半橋式逆變器,由于開(kāi)關(guān)管固有開(kāi)關(guān)時(shí)間ts的影響,開(kāi)通時(shí)間ton往往小于關(guān)斷時(shí)間toff,因此容易發(fā)生同臂兩只開(kāi)關(guān)管同時(shí)導(dǎo)通的短路故障。為了避免這種故障的發(fā)生,通常要設(shè)置開(kāi)關(guān)死區(qū)△t,以保證同橋臂上的一只開(kāi)關(guān)管可靠關(guān)斷后,另一只開(kāi)關(guān)管才能開(kāi)通。死區(qū)的設(shè)置方式有兩種:一種是提前關(guān)斷、延滯開(kāi)通的雙邊對(duì)稱(chēng)設(shè)置;另一種是按時(shí)關(guān)斷、延滯△t開(kāi)通的單邊不對(duì)稱(chēng)設(shè)置。典型的電壓型三相SPWM半橋式逆變器如圖1(a)所示。其中圖1(b)是死區(qū)對(duì)稱(chēng)設(shè)置時(shí)的波形圖;圖1(c)是死區(qū)不對(duì)稱(chēng)設(shè)置時(shí)的波形圖。在這兩種波形圖中,uAO為相與直流電源中點(diǎn)“0”之間的理想電壓波形(載波比),uAO′為設(shè)置死區(qū)時(shí)的電壓波形。![]()
![]()
![]()
![]() 在感性負(fù)載時(shí),當(dāng)V1導(dǎo)通時(shí)A點(diǎn)為,當(dāng)V4導(dǎo)通時(shí)A點(diǎn)為。在死區(qū)△t內(nèi)V1和V4都不導(dǎo)通時(shí),感性負(fù)載使D1和D4續(xù)流以保持電流iA連續(xù)。當(dāng)iA為正時(shí)D4續(xù)流,A點(diǎn)與直流電源負(fù)極接通,A點(diǎn)電位為;當(dāng)iA為負(fù)時(shí)D1續(xù)流,A點(diǎn)與直流電源正極接通,A點(diǎn)電位為,這樣就產(chǎn)生了誤差電壓uD1.4。uD1.4與uAO′疊加就產(chǎn)生出實(shí)際輸出電壓uAO″。比較uAO″與uAO可知,實(shí)際輸出電壓發(fā)生了畸變。在iA為正時(shí)所有正脈沖寬度都減小△t,所有負(fù)脈沖寬度都增加△t;在iA為負(fù)時(shí)所有負(fù)脈沖寬度都減小△t,所有正脈沖寬度都增加△t。這是由死區(qū)△t內(nèi)的二極管續(xù)流造成的,畸變后的實(shí)際輸出電壓波形如圖中uAO″所示。
在感性負(fù)載時(shí),當(dāng)V1導(dǎo)通時(shí)A點(diǎn)為,當(dāng)V4導(dǎo)通時(shí)A點(diǎn)為。在死區(qū)△t內(nèi)V1和V4都不導(dǎo)通時(shí),感性負(fù)載使D1和D4續(xù)流以保持電流iA連續(xù)。當(dāng)iA為正時(shí)D4續(xù)流,A點(diǎn)與直流電源負(fù)極接通,A點(diǎn)電位為;當(dāng)iA為負(fù)時(shí)D1續(xù)流,A點(diǎn)與直流電源正極接通,A點(diǎn)電位為,這樣就產(chǎn)生了誤差電壓uD1.4。uD1.4與uAO′疊加就產(chǎn)生出實(shí)際輸出電壓uAO″。比較uAO″與uAO可知,實(shí)際輸出電壓發(fā)生了畸變。在iA為正時(shí)所有正脈沖寬度都減小△t,所有負(fù)脈沖寬度都增加△t;在iA為負(fù)時(shí)所有負(fù)脈沖寬度都減小△t,所有正脈沖寬度都增加△t。這是由死區(qū)△t內(nèi)的二極管續(xù)流造成的,畸變后的實(shí)際輸出電壓波形如圖中uAO″所示。
2實(shí)際輸出電壓uAO″的諧波分析
假定載波與調(diào)制波不同步,則在調(diào)制波各周期中所包含的脈沖模式就不相同,因此不能用調(diào)制波角頻

(a)電路圖

(b)死區(qū)雙邊對(duì)稱(chēng)設(shè)置時(shí)的波形圖

圖1有死區(qū)的三相半橋式SPWM逆變器
(c)死區(qū)單邊不對(duì)稱(chēng)設(shè)置時(shí)的波形圖
率ωs為基準(zhǔn),而應(yīng)當(dāng)用載波角頻率ωc為基準(zhǔn)。這樣,研究它的基波與基波諧波、載波與載波諧波及其上下邊頻的分布情況時(shí),就能很方便地用雙重傅立葉級(jí)數(shù)來(lái)表示: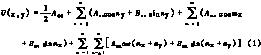
![]() 2.1死區(qū)雙邊對(duì)稱(chēng)設(shè)置時(shí)uAO′的諧波分析
2.1死區(qū)雙邊對(duì)稱(chēng)設(shè)置時(shí)uAO′的諧波分析
如圖1(b)所示,uAO′相當(dāng)于二極管不續(xù)流時(shí)輸出電壓的波形。載波三角波的方程式為:![]()
![]() 正弦調(diào)制波的方程式為:
正弦調(diào)制波的方程式為:
對(duì)于理想波uAO,二階SPWM波正脈沖前沿(負(fù)脈沖后沿)采樣點(diǎn)a為:![]()
![]() 令x=ωct;y=ωst;,則可得
令x=ωct;y=ωst;,則可得![]()
二階SPWM波負(fù)脈沖前沿(正脈沖后沿)采樣點(diǎn)b為:

圖2uAO′與uD1.4的向量相加和uAO″、uAO′、uD1.4的向量關(guān)系
![]()
![]()
![]()
![]() 對(duì)于圖1(b)中uAO′,在x=ωct的2πk-到2π(k+1)-區(qū)間內(nèi),可以得到二階SPWM波的時(shí)間函數(shù)為:
對(duì)于圖1(b)中uAO′,在x=ωct的2πk-到2π(k+1)-區(qū)間內(nèi),可以得到二階SPWM波的時(shí)間函數(shù)為:
![]() ,k=0,1,2,3…
,k=0,1,2,3…
經(jīng)分析可以得出:![]()
![]()
![]()
![]() uAO′=sinωst+Jo()cosm·
uAO′=sinωst+Jo()cosm·![]()
![]() sin(mNωst)-Jn()[cos(m+n)π-1]
sin(mNωst)-Jn()[cos(m+n)π-1]![]() cosmsin[(mN+n)ωst](2)
cosmsin[(mN+n)ωst](2)
2.2對(duì)死區(qū)雙邊對(duì)稱(chēng)設(shè)置時(shí)uD1.4的諧波分析
圖(1)b中誤差波uD1.4,其雙重傅立葉級(jí)數(shù)中的![]() (3)
(3)
對(duì)于載波及載波m次諧波的上下邊頻:![]() ;Bmn=0
;Bmn=0
2.3死區(qū)雙邊對(duì)稱(chēng)設(shè)置時(shí)uAO″的諧波分析
由圖1(b)可知,實(shí)際波uAO″等于有死區(qū)波uAO′與誤差波uD1.4之和。由于死區(qū)是雙邊對(duì)稱(chēng)設(shè)置,所以u(píng)AO′與調(diào)制波uS相位相同,電流iA滯后于uAO′一個(gè)φ角,而誤差波uD1.4又與iA相位相反,因此,uD1.4的相位超前于uAO′180°-φ,如圖(2)所示。因此,當(dāng)以u(píng)AO′的相位為基準(zhǔn)時(shí)可得:
uAO″=uAO′0°+uD1.4180°-φ(5)![]() uAO′與uD1.4的基波幅值uAO(1)′=;
uAO′與uD1.4的基波幅值uAO(1)′=;![]() ,由圖(2)可知:uAO″的基波幅值
,由圖(2)可知:uAO″的基波幅值![]() UAO(1)″的初相位角
UAO(1)″的初相位角![]() (6)
(6)
2.4死區(qū)單邊不對(duì)稱(chēng)設(shè)置時(shí)uAO″的諧波分析![]() 對(duì)于圖1(c),由于死區(qū)是不對(duì)稱(chēng)設(shè)置,即只在脈沖前沿設(shè)有死區(qū)△t,故uAO′滯后于調(diào)制波us的相位角為。但當(dāng)以u(píng)AO′的相位為基準(zhǔn)時(shí),uAO″、uAO′、uD1.4的相位關(guān)系與對(duì)稱(chēng)設(shè)置時(shí)相同,故按著與前面相同的方法可以得到:
對(duì)于圖1(c),由于死區(qū)是不對(duì)稱(chēng)設(shè)置,即只在脈沖前沿設(shè)有死區(qū)△t,故uAO′滯后于調(diào)制波us的相位角為。但當(dāng)以u(píng)AO′的相位為基準(zhǔn)時(shí),uAO″、uAO′、uD1.4的相位關(guān)系與對(duì)稱(chēng)設(shè)置時(shí)相同,故按著與前面相同的方法可以得到:
uAO″=uAO′0°+uD1.4180°-φ(7)
3死區(qū)對(duì)輸出電壓波形影響的分析
無(wú)死區(qū)理想波uAO的雙重傅立葉級(jí)數(shù)方程式,可以用方程式(2)令△t=0得到: 當(dāng)死區(qū)雙邊對(duì)稱(chēng)設(shè)置時(shí),理想波uAO與實(shí)際波uAO″之間的偏差電壓udev由圖1(b),可知:
當(dāng)死區(qū)雙邊對(duì)稱(chēng)設(shè)置時(shí),理想波uAO與實(shí)際波uAO″之間的偏差電壓udev由圖1(b),可知:
udev=uAO0°-uAO″φ′
偏差電壓udev的相位與電流iA相同,與誤差電壓uD1.4相位相反。
udev=uAO0°-uAO′0°-uD1.4180°-φ(9)
將方程式(6)、(7)與方程式(8)比較可知,死區(qū)對(duì)輸出電壓的波形存在著明顯的影響,影響的大小與死區(qū)△t的值和載波比N有關(guān)。

圖3死區(qū)△t對(duì)基波幅值的影響

圖4載波比N對(duì)基波與諧波的影響
![]() ●死區(qū)△t的影響:空載時(shí)二極管不續(xù)流,死區(qū)對(duì)輸出電壓影響不大,感性負(fù)載時(shí)二極管續(xù)流產(chǎn)生誤差波uD1.4,使輸出電壓基波幅值減小,相位超前φ′角,并出現(xiàn)了幅值為的3、5、7……次諧波,死區(qū)△t越大,這種影響越大。
●死區(qū)△t的影響:空載時(shí)二極管不續(xù)流,死區(qū)對(duì)輸出電壓影響不大,感性負(fù)載時(shí)二極管續(xù)流產(chǎn)生誤差波uD1.4,使輸出電壓基波幅值減小,相位超前φ′角,并出現(xiàn)了幅值為的3、5、7……次諧波,死區(qū)△t越大,這種影響越大。
●載波比N的影響:方程(6)、(7)中的ωc=Nωs,所以當(dāng)N增大時(shí),輸出電壓基波幅值的減小和3、5、7……次諧波的增大更嚴(yán)重。![]() 輸出電壓uAO″方程中產(chǎn)生的3、5、7……次諧波,隨著N的增大而上升;而uAO″中的載波下邊頻產(chǎn)生的3、5、7……次諧波,隨著N的增大而減小。因此,輸出電壓uAO″中3、5、7……次諧波的總和,隨著N的增加呈現(xiàn)出先減小而后增大的變化,中間有一個(gè)使3、5、7……次諧波含量為最小的最佳載波比N。這就打破了SPWM逆變器隨著N的增大而使低次諧波含量減小的傳統(tǒng)理論。
輸出電壓uAO″方程中產(chǎn)生的3、5、7……次諧波,隨著N的增大而上升;而uAO″中的載波下邊頻產(chǎn)生的3、5、7……次諧波,隨著N的增大而減小。因此,輸出電壓uAO″中3、5、7……次諧波的總和,隨著N的增加呈現(xiàn)出先減小而后增大的變化,中間有一個(gè)使3、5、7……次諧波含量為最小的最佳載波比N。這就打破了SPWM逆變器隨著N的增大而使低次諧波含量減小的傳統(tǒng)理論。
4計(jì)算機(jī)輔助分析和實(shí)驗(yàn)曲線
4.1死區(qū)△t對(duì)輸出電壓基波幅值的影響
圖(3)給出了輸出頻率為40Hz、M=0.8、N=15、cosφ≈1和cosφ=0.8時(shí)基波幅值與死區(qū)△t的關(guān)系曲線,可以看出隨著△t的增大基波幅值下降,當(dāng)cosφ≈1時(shí)基波線性下降。
4.2載波比N對(duì)輸出基波電壓和3、5、7……次諧波的影響
圖(4)給出了輸出頻率為40Hz、M=0.8、△t=40μs、cosφ=0.8時(shí)基波幅值和3、5、7……次諧波幅值與載波比N的關(guān)系曲線,可以看出隨著N的增大基波幅值大幅度降低,當(dāng)N=99時(shí)基波幅值降低到理論值的37%;隨著N的增大,3、5、7……次諧波的幅值先是下降,當(dāng)N>15時(shí)開(kāi)始顯著上升。對(duì)于3次諧波,當(dāng)N=9時(shí)為最小,當(dāng)N>9時(shí)隨著N的增加顯著上升,當(dāng)N=99時(shí)上升到基波理論值的21%。由此圖可知N=15時(shí)是最佳載波比。
5結(jié)語(yǔ)
在SPWM逆變器中,設(shè)置死區(qū)△t對(duì)輸出電壓波形有明顯的影響:
(1)使輸出電壓基波幅值減小,并產(chǎn)生出與△tN成正比的3、5、7……次諧波。
(2)對(duì)于有死區(qū)的SPWM逆變器,隨著載波N的增大,輸出電壓uAO″中的3、5、7……次諧波幅值先是減小,當(dāng)N>15以后顯著增大。不像傳統(tǒng)理論中所說(shuō)的,隨著載波N的增大,低次諧波含量將逐漸減小的結(jié)論。![]() (3)對(duì)于變頻調(diào)速系統(tǒng),當(dāng)電機(jī)低速運(yùn)行時(shí)ωs減小,使載波比相應(yīng)增大,因此△t與N將使基波幅值減小,和3、5、7……次諧波增大的影響更加嚴(yán)重,在這種情況下,為了保證電機(jī)的正常運(yùn)轉(zhuǎn),必須對(duì)死區(qū)的不良影響進(jìn)行補(bǔ)償。
(3)對(duì)于變頻調(diào)速系統(tǒng),當(dāng)電機(jī)低速運(yùn)行時(shí)ωs減小,使載波比相應(yīng)增大,因此△t與N將使基波幅值減小,和3、5、7……次諧波增大的影響更加嚴(yán)重,在這種情況下,為了保證電機(jī)的正常運(yùn)轉(zhuǎn),必須對(duì)死區(qū)的不良影響進(jìn)行補(bǔ)償。

