0 引言

　　對于大多數(shù)無線傳感器網(wǎng)絡(luò)應(yīng)用來說，沒有位置信息的數(shù)據(jù)是毫無意義的,。無線傳感器網(wǎng)絡(luò)目標(biāo)定位跟蹤的前提是節(jié)點自身定位,。無線傳感器網(wǎng)絡(luò)節(jié)點定位算法可分為基于距離和距離無關(guān)兩大類，基于距離的定位算法主要有RSSI,、TOA,、TDOA、AOA 等,，距離無關(guān)的定位算法主要有質(zhì)心算法,、DV-hop 算法、凸規(guī)劃,、MDS-MAP 等,。

　　RSSI 測距無需額外硬件，實現(xiàn)簡單,，具備低功耗,、低成本等特點，應(yīng)用十分廣泛,。RSSI 的技術(shù)原理是已知錨節(jié)點發(fā)射信號的強(qiáng)度,，根據(jù)未知節(jié)點接收到的信號強(qiáng)度，利用信號傳播模型計算兩點的距離,。由于存在多徑,、干擾、遮擋等因素,，RSSI 測距的精度較低,，必須采用各種算法來減小測距誤差對定位精度的影響，因而提出了一種基于RSSI 測距的無線傳感器網(wǎng)絡(luò)距離修正定位算法,，可有效減小RSSI 測距誤差對節(jié)點定位精度的影響,。

　　1 算法模型

　　1.1 無線信號傳播模型

　　RSSI 測距使用的無線信號傳播模型包括經(jīng)驗?zāi)Ｐ秃屠碚撃Ｐ停碚撃Ｐ褪窃诖罅拷?jīng)驗?zāi)Ｐ蛿?shù)據(jù)的基礎(chǔ)上總結(jié)提煉而成的。

　　對于經(jīng)驗?zāi)Ｐ?，首先要按照一定的密度選取參考點,，建立信號強(qiáng)度與到某個信標(biāo)點距離的映射矩陣，在實際定位時根據(jù)測得的信號強(qiáng)度與映射矩陣進(jìn)行對比,，并采用數(shù)學(xué)擬合方式確定待測節(jié)點到錨節(jié)點的距離,。

　　無線信號傳播理論模型主要有自由空間傳播模型、對數(shù)距離路徑損耗模型,、對數(shù)-常態(tài)分布模型等,，其中對數(shù)-常態(tài)分布模型的使用最為廣泛。

　　對數(shù)-常態(tài)分布模型如式（1）所示：

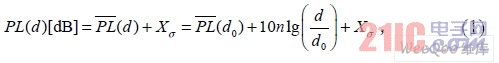
　　其中n 是路徑損耗指數(shù),，表明路徑損耗隨距離增長的速率,，范圍在2~6 之間。d0 為近地參考距離,，由測試決定,。式（1）能夠預(yù)測出當(dāng)距離為d 時接收到的平均能量。由于相同距離d 的情況下,，不同位置的周圍環(huán)境差距非常大因而引入了Xσ,，Xσ 是一個平均值為0 的高斯分布變量。

　　為了更好地描述距離修正定位算法,，這里提出兩個合理的假設(shè)條件：

　?、儆捎诟鞣N障礙物的影響，絕大多數(shù)實際情況中,，式（1）預(yù)測出的PL（d）[dB]比實際信號能量偏大,；②當(dāng)距離d 增大時，PL（d）[dB]與實際損耗能量的相對偏差也會增大,。

　　1.2 確定相交區(qū)域質(zhì)心的數(shù)學(xué)模型

　　已知三個節(jié)點A,、B、C 的坐標(biāo)為（xa, ya）,、（xb, yb）和（xc,yc）,，節(jié)點O到他們的距離為ra、rb 和rc,，假設(shè)節(jié)點O的坐標(biāo)（xo, yo）,，則（xo, yo）的數(shù)值可通過式（2）得出，也就是說以A,、B 和C 三點為圓心,，以ra、rb 和rc 為半徑作圓,，則三圓將相交與點O,，如圖1（a）所示。

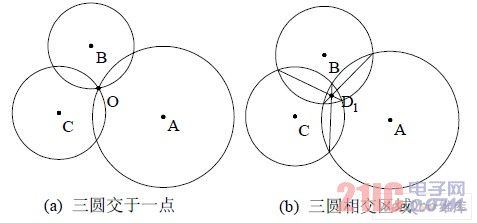
圖1 三圓相交情況。

　　但在實際情況中,，由于RSSI 測距存在誤差,，并且由于實際的路徑損耗比理論模型的數(shù)值偏大，也就是說測量出來的未知點到錨節(jié)點的距離d 總是大于實際距離r,。以A,、B和C 三點為圓心，以da1,、db1 和dc1 為半徑作圓,，三圓將不再相交于點O，而是存在一個相交區(qū)域,，如圖1（b）所示,。

　　三圓相交區(qū)域的邊界有三個交點，三點質(zhì)心為點D,。其中點D 的坐標(biāo)可以通過式（3）求解,。

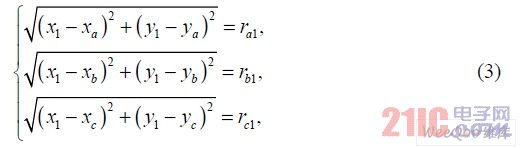
　　但是二次方程,，求解過程計算量較大,，因而文中采用如圖1（b）所示的點D1 的坐標(biāo)近似質(zhì)心D 的坐標(biāo)。三圓兩兩相交,，則三條交線將相交于點D1,。將式（2）中的方程式兩兩相減，則分別得到每條交線的直線方程,，D1 的坐標(biāo)則可以通過這些直線方程求解,，如式（4）。

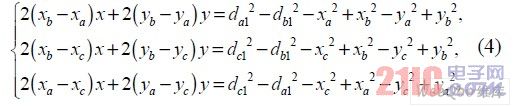
　　1.3 距離修正

　　在某些文章中,，以D1 的坐標(biāo)作為點O 的近似值,，其準(zhǔn)確度雖然比三邊定位等方法要高，但是還是可能存在較大的誤差,，尤其是當(dāng)da1,、db1、dc1 與ra,、rb 和rc 的相對誤差各不相同時尤其明顯,，因而需要對RSSI 方法測出的距離da1、db1和dc1 進(jìn)行修正,，然后再重復(fù)地求出新的三線交點D2 的坐標(biāo),，則可以用點D2 的坐標(biāo)作為點O 的近似坐標(biāo)。

　　設(shè)點A,、B 和C 到D1 的距離la1,、la2 和la3，則總體修正系數(shù)如式（5）所示。

　　根據(jù)1.1 節(jié)中假設(shè)②,，距離越遠(yuǎn)測距相對誤差越大,，則其修正程度越大，則da1 的修正系統(tǒng)如式（6）所示,，db1 和dc的修正系數(shù)類似,。

　　修正后的距離da2 通過式（7）得出，db2 和dc2 類似,。

　　2 算法流程

　　算法流程如下：

　?、俑麇^節(jié)點以相同功率周期性地向周圍廣播定位信息，信息中包括節(jié)點ID 和坐標(biāo),。普通節(jié)點收到定位信息后,，計算同一錨節(jié)點的RSSI 平均值；

　?、诋?dāng)普通節(jié)點收集到一定數(shù)量的錨節(jié)點信息時,，不再接收新信息。各普通節(jié)點根據(jù)RSSI 從強(qiáng)到弱對錨節(jié)點排序,，由式（1）求出節(jié)點到錨節(jié)點的距離,；

　　③選取距離最近的3 個錨節(jié)點,；

　?、芡ㄟ^式（4）計算三線交點D1 坐標(biāo)；

　?、莘謩e計算3 個錨節(jié)點與交點的距離,；

　　⑥通過式（5）計算總體修正系數(shù),；

　?、咄ㄟ^式（6）分別計算各自的修正系數(shù)，然后通過式（7）計算修正后的距離,；

　?、嘣俅瓮ㄟ^式（4）計算修正后的三線交點D2 的坐標(biāo)，D2的坐標(biāo)即為點O 的近似值,。

　　3 仿真分析

　　用MATLAB 進(jìn)行算法仿真,，基本初始條件是無線傳感器網(wǎng)絡(luò)位于100 m×100 m 的區(qū)域內(nèi)，該區(qū)域左下角為（0,，0）,，右上角為（100，100）,。區(qū)域內(nèi)均勻部署4,、9,、16、25個錨節(jié)點,，其中部署16 個錨節(jié)點的位置如表1 所示,。

　　未知節(jié)點隨機(jī)分布在區(qū)域內(nèi)，路徑損耗系數(shù)設(shè)為2.4,，每次仿真實驗進(jìn)行500 次,，仿真結(jié)果取500 次的平均值，各次仿真實驗結(jié)果如表2 所示,。

表1 16 個錨節(jié)點位置坐標(biāo)

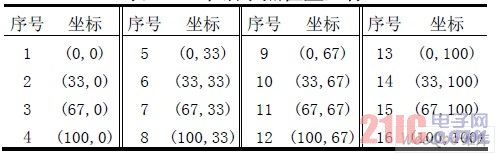
表2 仿真結(jié)果

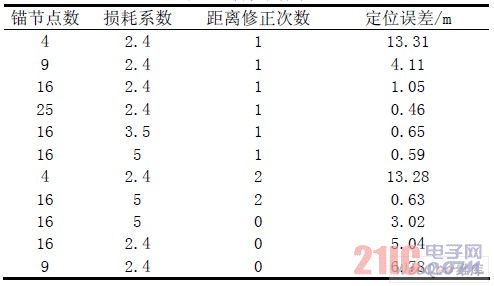
　　從仿真結(jié)果可以看出,，當(dāng)錨節(jié)點數(shù)目較少時，增加錨節(jié)點數(shù)量可以顯著提高定位精度,。路徑損耗系統(tǒng)對定位精度也有影響,，路徑損耗系統(tǒng)越大，定位精度越高,。從表2 可以看出,，距離修正次數(shù)增多對定位精度沒有顯著的影響，也就是說一般情況下只需要進(jìn)行一次距離修正即可,，采用距離修正與不采用距離修正相比,，定位精度明顯提高。

　　4 結(jié)語

　　無線傳感器網(wǎng)絡(luò)基于RSSI 測距的定位算法由于實現(xiàn)簡單,，應(yīng)用十分廣泛,。但由于RSSI 測距的精度不高，降低了節(jié)點定位精度,。基于RSSI 的無線傳感器網(wǎng)絡(luò)距離修正定位算法利用RSSI測距,，通過確定相交區(qū)域近似質(zhì)心,，以此為參考點對距離進(jìn)行修正，然后確定未知節(jié)點位置,。仿真結(jié)果表明,，該算法對測距誤差具有較高的容忍程度，并且具備很高的定位精度,。如圖2 所示,，三圓相交還存在無3 個交點的情況，下一步工作將詳細(xì)研究圖2所示各種情況對該算法的影響,，從而對算法進(jìn)行改進(jìn)完善,。

圖2 三圓相交區(qū)域無3 個交點的情況