1 RS碼的結(jié)構(gòu)

碼字長度為N=q-1(q=2i),，生成多項(xiàng)式為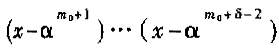,，αi∈GF(q)的RS碼有最小碼距δ=2t+1，能夠糾正t個(gè)隨機(jī)或突發(fā)錯(cuò)誤[1],。本文列舉的方案測(cè)試中采用的RS碼主要參數(shù)為N=255,、m0=0、t=8,，其中GF（2 8）的生成多項(xiàng)式為g（x）=x8+x4+x3+x2+1,。由于RS碼的編碼邏輯結(jié)構(gòu)比較簡單，文中僅給出仿真結(jié)果,。

2 RS碼的譯碼算法

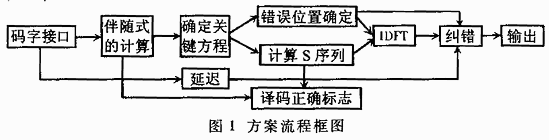
RS譯碼算法一般分為三步：伴隨式計(jì)算,、關(guān)鍵方程獲得和錯(cuò)誤圖樣的求解。其中關(guān)鍵方程的獲得是RS譯碼中最困難,、最為關(guān)鍵的一步,。

在利用伴隨式求解關(guān)鍵方程時(shí)，BM算法和Euclidean（歐氏）算法是兩種較好的選擇,。BM算法涉及大量的變量存儲(chǔ)和復(fù)雜的邏輯控制,，適用于軟件編程而不適合硬件實(shí)現(xiàn)。歐氏算法數(shù)據(jù)存儲(chǔ)量少,、控制便捷,，適合硬件實(shí)現(xiàn)。且采用歐氏算法確定關(guān)鍵方程所需時(shí)間與錯(cuò)誤個(gè)數(shù)成正比,，因此從處理時(shí)間上考慮,，歐氏算法也是較好的選擇,。

在獲得關(guān)鍵方程后，采用時(shí)域處理方法,，需要大量的運(yùn)算單元和控制電路,，在硬件實(shí)現(xiàn)中是不可取的。而采用頻譜結(jié)構(gòu)分析方法,，利用最短線性移位寄存器綜合及離散傅氏逆變換進(jìn)行處理,，邏輯簡單、耗時(shí)少,，適合硬件實(shí)現(xiàn),。雖然在傅氏變換時(shí)需要較多的邏輯單元，但對(duì)GF（2n）在n<10的情況下,，變換域譯碼器要比時(shí)域譯碼器簡單得多,。因而本文提出歐氏算法和頻譜結(jié)構(gòu)分析相結(jié)合的方案，并在實(shí)踐中獲得了較好的效果,。

Euclidean算法[3]步驟如下：

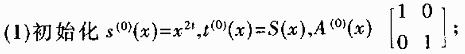
（2）按所列方法進(jìn)行迭代

3 方案流程

方案流程框圖如圖1所示,。

3.1 伴隨式S0,S1,…，S2t-1的計(jì)算

令r1,r2,，…,，rn為接收到的RS碼字，根據(jù)系統(tǒng)碼監(jiān)督矩陣的特性,，可構(gòu)造如圖2所示伴隨式計(jì)算電路Si=（（（r1αi+r2）αi+r3）αi…+rn,，從而實(shí)際伴隨式序列的計(jì)算。

    3.2 利用伴隨式確定關(guān)鍵方式    伴隨式的計(jì)算結(jié)果：S15,，S14,，…，S1,，S0為（FD,，8D），CE,，4A,，51，B2,，A1,，CA，C4,，0D,，73，56,，A6,，F(xiàn)5,，01），圖6和圖7中的sp即為S15,。    系統(tǒng)仿真表明,，譯碼器獲得的錯(cuò)誤位置和錯(cuò)誤圖案與實(shí)際假設(shè)的錯(cuò)誤位置（105，106,，107,，108，109,，110,，111）和錯(cuò)誤值（01）HEX完全一致。

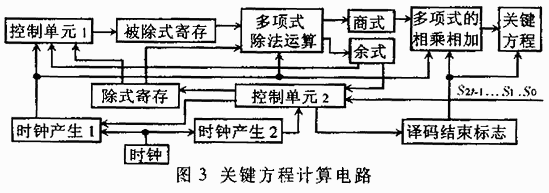
Euclidean算法的難點(diǎn)主工在于迭代計(jì)算過程中存在的被除數(shù)多項(xiàng)式和除數(shù)多項(xiàng)式長度的不確定性,，使每次計(jì)算中產(chǎn)生的商序列的長度不等，以及因此可能涉及到的不定長多項(xiàng)式的相乘和相加問題,，增加了硬件設(shè)計(jì)的難度,。系統(tǒng)采用了嵌套雙循環(huán)的方法，利用'時(shí)鐘產(chǎn)生2'控制外循,，'時(shí)鐘產(chǎn)生1'控制內(nèi)循環(huán),，從而優(yōu)化了算法，得到了問題的解決方案,。在獲得伴隨式的基礎(chǔ)上,，圖3電路可具體完成Euclidean算法對(duì)關(guān)鍵方程的求解σ（x）=σtxt+σt-1xt-1+…+σ1x+1。

3.3 利用最短線性移位寄存器綜合和離散傅氏變換獲取錯(cuò)誤圖樣

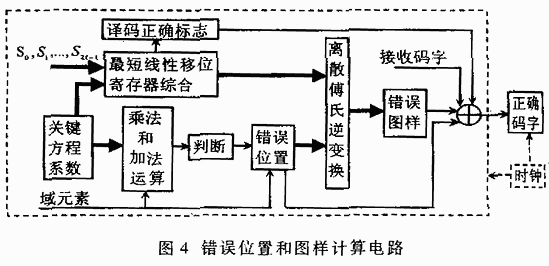
在得到關(guān)鍵方程后,，首先應(yīng)進(jìn)行錯(cuò)誤位置（關(guān)鍵方程的根）的確定,，這樣可減小電路的規(guī)模；利用錢搜索[1]（工程上求解σ（x）根的實(shí)用方法）的方法可以簡捷的確定錯(cuò)誤位置,。然后,，啟動(dòng)最短線性移位寄存器綜合和離散傅氏逆變換，經(jīng)過N次（運(yùn)算所在域的長度）迭代,，即可求得對(duì)應(yīng)各個(gè)錯(cuò)誤位置的錯(cuò)誤圖樣,，如圖4所示。用錯(cuò)誤圖樣對(duì)接收碼字進(jìn)行糾錯(cuò),，就可得到正確的信息序列,。

3.4 RS編譯碼在FPGA上的實(shí)現(xiàn)

有限域的乘法、加法運(yùn)算單元和各模塊的控制邏輯設(shè)計(jì)是系統(tǒng)成功的關(guān)鍵,。涉及有限域的各個(gè)運(yùn)算單元的運(yùn)算速度制約了譯碼器的速度,，而控制邏輯引導(dǎo)了譯碼的流程。硬件電路的軟件開發(fā)工具給設(shè)計(jì)復(fù)雜電路提供了簡捷思路,。系統(tǒng)采用了QUARTUS與第三方軟件相結(jié)合的方法,，用VHDL語言設(shè)計(jì)了大部分功能模塊,。特別是在乘法器設(shè)計(jì)中，乘數(shù)確定,、被乘數(shù)不定的有限域乘法器,，經(jīng)邏輯綜合和優(yōu)化設(shè)計(jì)后，運(yùn)算速度可分別在6.8ns和11.6ns內(nèi)完成,，完全可以滿足系統(tǒng)符號(hào)速率50Mbps的要求,。應(yīng)該指出，系統(tǒng)速度的進(jìn)一步提高受到求逆運(yùn)算的限制,，求逆運(yùn)算沒有明確的數(shù)學(xué)結(jié)構(gòu)（通常采用查表的方法）,，這是制約運(yùn)算速度的瓶頸。但針對(duì)流式譯碼算法,，上述結(jié)構(gòu)已能滿足要求,。

4 仿真結(jié)果

4.1 編碼器的仿真

仿真的時(shí)鐘頻率為50MHz，在EN為高電平時(shí)輸入信息有效,。為簡單起見,，采用系統(tǒng)碼的縮短型，即信息為（00,，00,，…，00,，02,，01，02）.編碼器的仿真結(jié)果如圖5所示,。其中,，IN為輸入信息，CLK為系統(tǒng)時(shí)鐘,，C為編碼輸出（輸入和輸出均為16進(jìn)制）,。

4.2 譯碼器的仿真

首先，給出系統(tǒng)的仿真全貌,，如圖6所示,。其中C為接收到的RS碼，SP為伴隨式S15,shang為運(yùn)用歐氏算法得到的商序列,，SeryDA為S序列,，anssd和ERTD分別對(duì)應(yīng)碼字可能存在的第四個(gè)錯(cuò)誤位置和錯(cuò)誤值，仿真中的接收碼在位置（105,，106,，107，108,，109,，110,，111，112）上錯(cuò)誤均為（01）HEX,。

 

這里重點(diǎn)給出利用伴隨式計(jì)算關(guān)鍵方程的電路仿真結(jié)果,，如圖7所示。當(dāng)輸入伴隨式結(jié)果以后,，運(yùn)算電路啟動(dòng),，在計(jì)算商序列的同時(shí)進(jìn)行聯(lián)接多項(xiàng)式的迭代運(yùn)算。歐氏算法的商序列shang為：（FF,，58）,，（37，92）,，（50,，45），（E9,，C7）,，（F4，B9）,，（5D，33）,，（87,，8F）。當(dāng)滿足終止條件以后顯示標(biāo)志QQC,，同時(shí),，給出關(guān)鍵方程系數(shù)如圖7中（AI，AH,，AG,，AF，AE,，AD,，AC，AB,，AA）即（00,，19，2E,，EC,，A8，AD,，41,，E6,，95），對(duì)應(yīng)有限域上的表達(dá)式為：

δ（x）=α193x7+α130x6+α122x5+α144x4+α252x3+α191x2+α160x+α184;有解為（α105,，α106,，α107，α108,，α109,，α110，α111）,，與假定錯(cuò)誤位置完全一致,。然后求解S序列，同時(shí)針對(duì)各錯(cuò)誤位置進(jìn)行IDFT,，就可以得到對(duì)應(yīng)的錯(cuò)誤值,。圖6中anssd和ERTD表示位置108上存在的錯(cuò)誤為（01）HEX。

圖5 編碼器仿真結(jié)果

基于APEX架構(gòu)的可編程單芯片RS編譯碼硬件解決方案在中國普天集團(tuán)西安藍(lán)牙通訊設(shè)備有限公司的二次群無線擴(kuò)頻通信機(jī)的改造項(xiàng)目中得到了應(yīng)用,。它可用于離散譯碼,、流式譯碼，在添加一級(jí)緩存的基礎(chǔ)上,，同樣適用于連續(xù)譯碼,。