摘 要： 為了提高MIMO-OFDM系統(tǒng)的數(shù)據(jù)傳輸率和頻譜利用率,，提出一種新的自適應算法,。該算法在保證信道質(zhì)量所需誤碼率和總發(fā)射功率的前提下，按照各個子載波衰落程度動態(tài)地分配比特和功率,，使系統(tǒng)的總數(shù)據(jù)傳輸速率最大,。理論分析得出，該算法降低了系統(tǒng)運算復雜度,，能很大地改善系統(tǒng)的整體性能。
關鍵詞： MIMO-OFDM,；自適應,；功率分配；比特分配
為了提高移動通信的數(shù)據(jù)傳輸速率,，MIMO-OFDM技術應運而生,。MIMO-OFDM技術結(jié)合了正交頻分復用OFDM（Orthogonal Frequency Division Multiplexing）和多輸入多輸出MIMO（Multiple Input Multiple Output）兩種技術的優(yōu)點，利用時間,、頻率和空間三種分集技術,，不僅可以提高頻譜利用率，增大系統(tǒng)容量,，還可以有效地克服多徑效應和頻率選擇性衰落,，在技術上相互補充、相得益彰，為新一代移動通信中最有前途的技術之一[1-4],。
1 MIMO-OFDM系統(tǒng)的自適應技術
1.1 自適應技術
在多用戶情況下,，如何為每個用戶最優(yōu)地分配系統(tǒng)資源，從而使系統(tǒng)的發(fā)送功率最低或者使系統(tǒng)的傳輸速率最高,，是一個非常復雜的問題,。MIMO-OFDM技術雖然具有很多優(yōu)點，但每個子載波上的衰落程度不同,，其誤碼率主要由經(jīng)歷衰落最嚴重的子信道決定,。在MIMO-OFDM系統(tǒng)中使用自適應技術可以根據(jù)子載波衰落情況對各個子載波動態(tài)地分配發(fā)送功率和信息比特數(shù)，以最大限度地提高系統(tǒng)容量,。自適應技術可大大提高系統(tǒng)的傳輸容量和傳輸性能,，從而優(yōu)化系統(tǒng)性能[5]。
2 自適應算法
在MIMO-OFDM系統(tǒng)中采用自適應技術時,，很重要的問題就是功率比特分配問題,。通常對此內(nèi)容的研究主要從三個角度出發(fā)：(1)在保證給定的性能和要求的數(shù)據(jù)速率下，使系統(tǒng)的總發(fā)射功率最??；(2)在給定發(fā)射功率和數(shù)據(jù)速率下，使系統(tǒng)最??；(3)在一定的總發(fā)射功率和目標下，使系統(tǒng)BER的總數(shù)據(jù)速率最大,。目前國內(nèi)外已經(jīng)有了不少關于自適應算法的研究,，最具代表性的有Chow算法、Fischer算法等,。在這些算法中,，主要是運算復雜度和系統(tǒng)性能兩者之間的矛盾，即運算復雜度越高系統(tǒng)性能越好,。
2.1 Fischer算法
Fischer算法是在Chow算法的基礎上改進的算法,，是犧牲一部分系統(tǒng)性能來降低復雜度。與Chow算法根據(jù)各個子載波的信道容量分配比特不同,，F(xiàn)ischer算法是在維持恒定傳輸速率和給定總發(fā)射功率的前提下,，使得系統(tǒng)的性能達到優(yōu)化[7-8]。Fischer算法的步驟如下：
2.2 基于MIMO-OFDM系統(tǒng)的自適應算法
在滿足一定MIMO-OFDM系統(tǒng)性能的條件下,，合適的自適應算法應該是性能和復雜度的折中,。本文提出一種新的MIMO-OFDM系統(tǒng)自適應算法，該算法是在保證一定的總發(fā)射功率和目標下,，使系統(tǒng)的總數(shù)據(jù)速率最大,，其數(shù)學表達式為：
其中,，H(k)代表第k個子載波上的信道頻域增益。在該算法中bk=0,，1,，2，4,，6,，它們分別對應不傳輸、BPSK,、QPSK,、16QAM和64QAM五種調(diào)制方式。對于多進制調(diào)制,，隨著進制數(shù)M的增大,，相應的傳輸效率也會增加，但是調(diào)制方式的抗干擾性能會有所下降,。在調(diào)制進制數(shù)M相同時,，MQAM調(diào)制具有最高的數(shù)據(jù)吞吐量。在實際設計中可以在信道質(zhì)量較差的時候,，采用性能較好的低階調(diào)制方式(如QPSK),；在信道質(zhì)量較好時，采用高階調(diào)制方式(如16QAM),，從而提供高速率傳輸和高頻譜利用率,。BPSK、QPSK,、16QAM和64QAM的誤碼率公式分別為[9]：
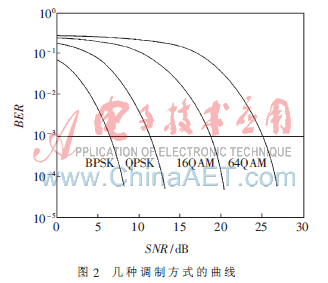
自適應算法的基本過程如圖3所示,。首先設定一個系統(tǒng)可承受的目標誤碼率λ，假設目標誤碼率為10-3,，把10-3代入式(5)計算BPSK,、QPSK、16QAM及64QAM四種調(diào)制方式在此誤碼率下的各個信噪比門限值γ0,、γ1,、γ2、γ3,；接著利用式(4)計算每個子載波上的信噪比SNRk,，為了選擇每一個子載波上的調(diào)制方式,，拿SNRk與各門限值一一比較,，當SNRk≥γ0時，可以根據(jù)SNRk落入的門限區(qū)間來選擇相應的調(diào)制方式,，例如γ0≤SNRk<γ1,，子載波k上就選用BPSK作為調(diào)制方式,。而當SNRk<γ0時，說明此時的信道情況很惡劣,，所以子載波k上不進行傳輸并不斷根據(jù)變化的信道狀態(tài)信息重復上述過程,；然后根據(jù)選擇的調(diào)制方式對每個子載波分配相應的比特數(shù)，例如16QAM調(diào)制方式分配4個比特,；最后再對每一個子載波進行功率分配,，即：
3 仿真結(jié)果及分析
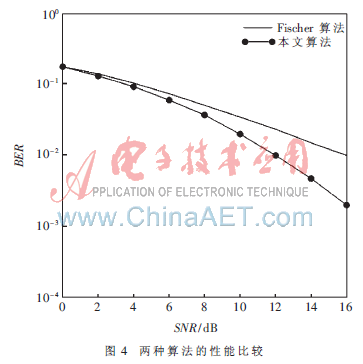
在Matlab仿真軟件平臺上對Fischer算法與本文提出算法間的性能進行了仿真比較。圖4為Fischer算法與本文提出算法間的性能比較,。本文提出算法只需根據(jù)各個子載波的信道衰落用預先確定的信噪比門限選定各個子載波的調(diào)制方式,，不需要任何迭代過程，因此算法復雜度比Fischer算法大為降低,。從圖中可看出在相同SNR下,，本文提出算法能得到更低的誤碼率。
在MIMO-OFDM系統(tǒng)中,，如果采用固定電平(m=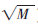
)調(diào)制方案,，例如16QAM調(diào)制方式，可知每個子載波都攜帶4個碼元,，那么各個子載波所分配到的功率也都相同,。為了保證系統(tǒng)的誤碼率性能，只能根據(jù)衰減最大的子信道來決定功率的分配,，這樣對信道資源造成了浪費,。如果采用自適應調(diào)制方案，信噪比大的子載波就會分配到較多的比特數(shù),，而那些信噪比較小的子載波就會分配到較少的比特數(shù),，甚至幾個信道質(zhì)量特別差的子載波不傳輸任何比特。根據(jù)上述分析,，該算法在保證信道質(zhì)量所需誤碼率和總發(fā)射功率的前提下,，按照各個子載波衰落情況動態(tài)地分配比特和功率，使系統(tǒng)的總數(shù)據(jù)速率最大,，很好地改善了系統(tǒng)的整體性能,。
為了增強MIMO-OFDM系統(tǒng)的整體性能，提供高數(shù)據(jù)傳輸率和高頻譜利用率,，避免資源浪費,，本文提出一種新的自適應算法。該算法在信道傳輸質(zhì)量滿足一定系統(tǒng)誤碼率和總發(fā)射功率下,，根據(jù)信道狀態(tài)信息自適應地使每個子載波的調(diào)制方式在BPSK,、QPSK、16QAM和64QAM之間自如切換,，動態(tài)地分配比特和功率,，使系統(tǒng)的總數(shù)據(jù)速率最大,。理論分析得出，在滿足MIMO-OFDM系統(tǒng)性能條件下,，該算法能夠降低系統(tǒng)運算復雜度,，并使系統(tǒng)的整體性能得到了優(yōu)化，體現(xiàn)出該算法的優(yōu)越性,。
參考文獻
[1] 王文博,，鄭侃.寬帶無線通信OFDM技術[M].北京：人民郵電出版社，2003.
[2] 佟學儉,，羅濤.OFDM移動通信技術原理與應用[M].北京：人民郵電出版社,，2003.
[3] 尹長川，羅濤,，樂光新.多載波寬帶無線通信技術[M].北京：北京郵電大學出版社,，2004.
[4] 謝顯中，李祥明,，唐宏,，等.基于TDD的第四代移動通信技術[M].北京：電子工業(yè)出版社，2005.
[5] 樊凌雁,，何晨,，馮國瑞.MIMO-OFDM系統(tǒng)下的自適應迭代比特分配算法[J].通信學報，2007,，28(11)：65-70.
[6] ALAMOUTI S M．A simple transmit diversity technique for wireless communications[J]．IEEE Trans．on Commun,，1998，2(4)：1451-1458．
[7] CHOW P S,，CIOFFI J M,，BINGHAM J A C．A practical discrete multitone transceiver loading algorithm for data transmission over spectrally shaped channels[J]．IEEE Trans． on Commun．，1995,，43(2)：773-775．
[8] FISCHER R F H,，HUBER J B.A new loading algorithm for discrete multitone transmission[A]．In：IEEE Globecom[C]．London，UK：1996：724-728．
[9] 王福昌,，熊兆飛,，黃本雄.通信原理[M].北京:清華大學出版社，2006.