電子干擾是現(xiàn)代電子戰(zhàn)的重要組成部分,，包括無源干擾和有源干擾，其中,，有源干擾可以分為欺騙干擾和遮蔽干擾,。欺騙干擾是采用假的目標(biāo)和信息作用于雷達(dá)的目標(biāo)檢測和跟蹤系統(tǒng)，使雷達(dá)不能正確的檢測真實(shí)目標(biāo)或者不能正確的測量真正目標(biāo)的參數(shù)信息,，從而達(dá)到迷惑或擾亂雷達(dá)對真正目標(biāo)檢測和跟蹤的目的,。遮蓋式的干擾是使用噪聲或類似噪聲的干擾信號" title="干擾信號">干擾信號遮蓋或淹沒有用信號，阻止雷達(dá)檢測目標(biāo)信息,。對于欺騙干擾可以使用與雷達(dá)信號的識別方法對其進(jìn)行檢測設(shè)別,，但是對于使用噪聲調(diào)制的遮蔽干擾信號，因?yàn)槠渥陨淼膹?qiáng)隨機(jī)性,，很難使用雷達(dá)信號的檢測識別方法,。但是由于干擾信號是時間上連續(xù)的信號，在一定的時間內(nèi)采樣的數(shù)目可以很大;而對雷達(dá)來說,，積累個數(shù)受到目標(biāo)照射時間和脈沖間隔的限制,，這是干擾噪聲檢測的優(yōu)勢所在，也成為了尋求檢測遮蔽干擾信號的突破口,。
1 噪聲調(diào)頻信號" title="調(diào)頻信號">調(diào)頻信號功率譜" title="功率譜">功率譜檢測原理
噪聲調(diào)頻" title="噪聲調(diào)頻">噪聲調(diào)頻干擾信號最常見的是射頻振蕩的頻率與調(diào)制噪聲電壓ξ(t)成線性關(guān)系,，為了方便把噪聲調(diào)頻，信號的時域如式(1)
設(shè)調(diào)制噪聲電壓ξ(t)是高斯噪聲,，其幅度概率密度分布為高斯函數(shù)
由于噪聲調(diào)頻干擾的角頻率與ξ(t)呈線性關(guān)系,，故瞬時角頻率或角頻偏的概率密度也應(yīng)為高斯分布，其均方根的值為
式(6)中的積分只有在mfe》1和mfe《1時才能近似求解,。
當(dāng)mfe》1可以得到噪聲調(diào)頻信號的干擾帶寬(半功率帶寬)為
對于噪聲調(diào)頻信號,，由于信號的隨機(jī)性很強(qiáng),，很難在使用相關(guān)的辦法對這類噪聲調(diào)制的信號進(jìn)行檢測，所以常用的瞬時相關(guān),、時頻分布等檢測方法對其無效,。但是由于接收系統(tǒng)在設(shè)計(jì)時，其系統(tǒng)的熱噪聲" title="熱噪聲">熱噪聲相對比較穩(wěn)定,，所以其熱噪聲功率譜也是相對穩(wěn)定的,。當(dāng)由調(diào)頻干擾信號進(jìn)入接收機(jī)時，根據(jù)式(6),，其功率譜在干擾頻帶 [f0一△fj/2,，f0+△fj/2]內(nèi)會比無調(diào)頻干擾信號時在能量上有明顯的提高，根據(jù)這一特征,，可以檢測出干擾信號,。并相應(yīng)的確定帶寬和中心頻率，如圖l所示,。
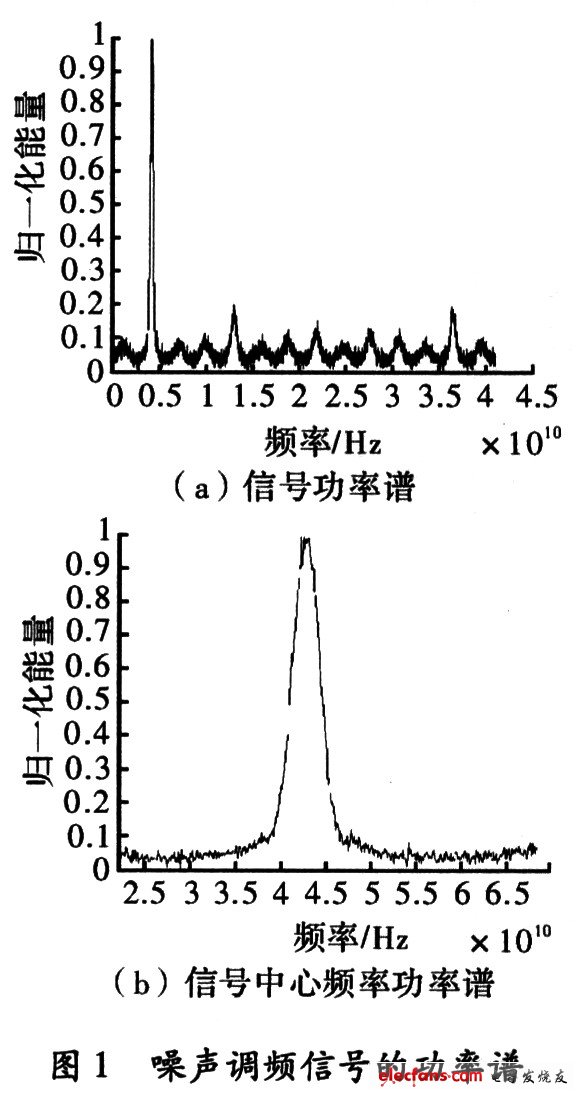圖1中噪聲調(diào)頻信號的中心頻率4.3 GHz,，每伏調(diào)制為1 GHz/V，時長10 ms,，為了提高檢測帶寬按單次時長100 ns做4 096采樣,，循環(huán)10 000次累積處理。在實(shí)用的條件下一般會至少做到幾十毫秒的時長來進(jìn)行累計(jì),。產(chǎn)生的白噪聲" title="白噪聲">白噪聲調(diào)制信號首先經(jīng)過256階的帶通濾波器,，用來給生成的白噪聲濾波進(jìn)行色化處理，通帶為4.29～4.31 GHz,，所以視頻調(diào)頻帶寬20 MHz,。經(jīng)過濾波后的隨機(jī)數(shù)帶入到式(1)，得到噪聲調(diào)頻信號,，然后計(jì)算功率譜,，結(jié)果如圖1(a)所示。從圖1(a)中可以看到在40 GHz的檢測帶寬中,，信號的能量主要集中在4.3 GHz左右,。圖1(b)為中心頻率處放大圖形，可以看出干擾信號的3 dB帶寬(即歸一化能量的0.707左右處)為0.18 GHz,，10 dB帶寬(歸一化能量0.3左右處)為0.37 GHz,。
當(dāng)白噪聲累加到調(diào)頻干擾后在得到的功率譜，如圖2所示,。
從圖2中可以看出在SNR=一10 dB情況下,，可以檢測處噪聲調(diào)頻干擾信號，且在中心頻率處的能量有所衰減,。由于考慮仿真速度的需要此處所取時長較短,，如果加長時間的積累,，即相當(dāng)于增加了能量的積累，得到的檢測靈敏度會更高,。對于檢測門限的設(shè)定,，是在實(shí)際應(yīng)用中關(guān)心的問題。這里簡述兩種參考門限的確定方法,。第一,，對于系統(tǒng)的熱噪聲是在設(shè)計(jì)時所確定的固有性質(zhì)，相對外界環(huán)境要穩(wěn)定的多,，在設(shè)置門限時可以考慮當(dāng)切斷外來所有的信號輸入,，得到的機(jī)內(nèi)熱噪聲的功率均值數(shù)作為參考門限，這樣的好處是確保此時噪聲純凈,，缺點(diǎn)是沒有考慮環(huán)境噪聲的存在，從而出現(xiàn)虛警的概率增加,，這也是文中使用的方法;第二,，是在偵察天線沒有對準(zhǔn)干擾源的情況下，得到內(nèi)外混合噪聲的各個頻點(diǎn)的功率均值作為參考門限,，其優(yōu)點(diǎn)是能夠真實(shí)的反映實(shí)際情況,，但是如果此時有其它發(fā)射機(jī)信號的輸入，則檢測出現(xiàn)漏警的概率會大大增加,。
2 相似理論
在信號與系統(tǒng)學(xué)科中,，相關(guān)性是一種在時域中對信號特性進(jìn)行描述的重要方法。由于信號與其功率譜函數(shù)是一對傅里葉變換,，在信號分析中往往利用它來分析隨機(jī)信號的功率譜分布,，以致不少人一提到相關(guān)性馬上會聯(lián)想到信號功率譜的計(jì)算。假設(shè)得到的兩信號分別為X(t),，Y(t),。可以選擇當(dāng)倍數(shù)K使KY(t)去逼近 X(t),。在此可以借用誤差能量來度量波形的相似程度,。
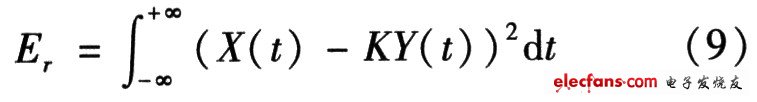
其中Er代表誤差能量，K的選擇是為了使誤差能量最小,，可以得出
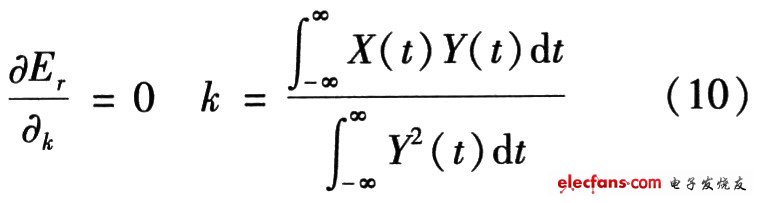
另外,，可定義相對誤差能量為
其中Pxy為相關(guān)系數(shù)?？梢酝瞥?/p>
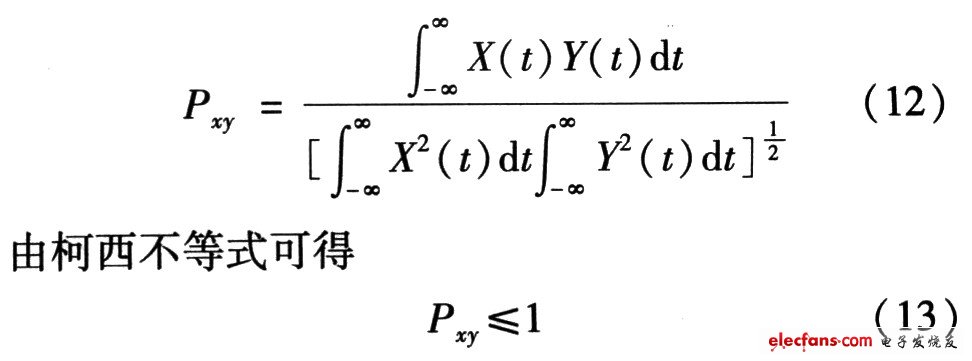
對于能量有限的信號而言,，能量是確定的，相關(guān)系數(shù)的大小只由X(t)*Y(t)積分決定,。若兩個完全不相似的信號,，其幅度取值和出現(xiàn)時刻是相互獨(dú)立,、彼此無關(guān)的，即X(t)*Y(t)=0,，其積分結(jié)果也為0,，所以當(dāng)相關(guān)系數(shù)為O時相似度最差，即不相關(guān),。當(dāng)相關(guān)系數(shù)為1時,，則誤差能量為0，說明這兩個信號相似度很好,，是線性相關(guān)的,。因此把相關(guān)系數(shù)作為兩個信號相似性的度量完全是有理論依據(jù)的、合理的,。
3 利用相似理論的噪聲調(diào)頻信號檢測
為了討論方便,，假設(shè)接收機(jī)為理想接收機(jī)，即在通帶內(nèi),，其幅頻特性為一固定值,，相頻為線性，而通帶之外增益為零,，中心頻率ω0為且遠(yuǎn)大于接收機(jī)帶寬△ω,，并假定背景噪聲是高斯白噪聲，這種假設(shè)不失一般性,，基本可以很好地描述常規(guī)接收機(jī)的檢測特性,。
在時長1 ms，信噪比從一10～10 dB進(jìn)行100次蒙特卡洛實(shí)驗(yàn),，其信號具體形式如第2節(jié)所述,，首先得到信號和基準(zhǔn)白噪聲的各自的功率譜，然后代入式(12)中,，計(jì)算其相關(guān)系數(shù),。考慮到虛警的可能性,，通常認(rèn)為當(dāng)相關(guān)系數(shù)<0.8時存在噪聲調(diào)頻干擾,，否則沒有噪聲干擾信號進(jìn)入。所得結(jié)果,，如圖3所示,。
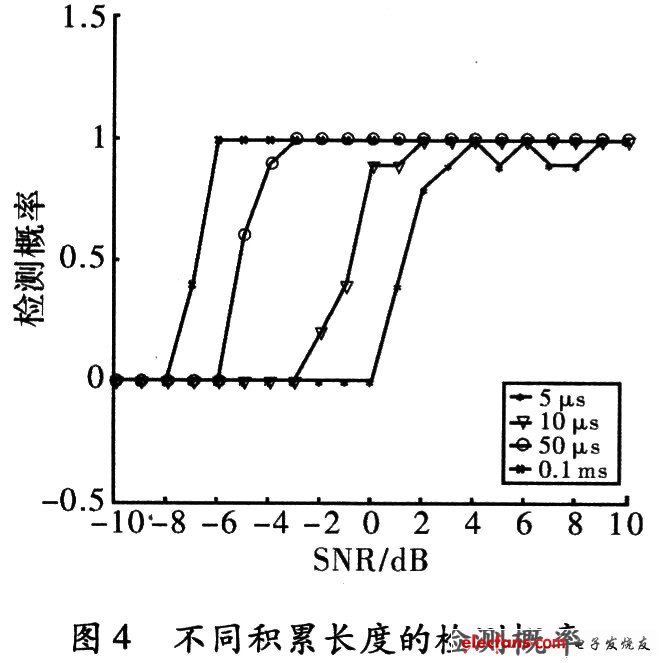
從圖3可以看出在信噪比一3 dB以上能夠在時長0.1 ms下做到100%的檢測。充分說明了該方法對檢測識別噪聲調(diào)頻信號是可行的,。而且根據(jù)積累時長的不同,，對算法檢測的靈敏度影響很大，在圖4給出了不同積累時間10次蒙特卡洛實(shí)驗(yàn)的檢測概率,。從圖4中可以看出,，隨著時長的增加不但檢測靈敏度有比較明顯的提高,，同時檢測曲線更加的平滑，誤差減小,。
4 結(jié)束語
由于噪聲調(diào)頻信號的強(qiáng)隨機(jī)性,，利用相關(guān)的各種檢測方法無法對此類信號做出有效的檢測。文中利用功率譜積累和相似函數(shù)的方法對噪聲調(diào)頻信號進(jìn)行了檢測,，通過仿真試驗(yàn)驗(yàn)證了方法的可行性,，說明檢測概率與信噪比和累計(jì)時間長度的關(guān)系。