1 非單點模糊推理系統(tǒng)(NSFIS)
提出的制導(dǎo)炸彈智能控制系統(tǒng)的核心是非單點模糊推理系統(tǒng)(NSFIS)。一個n輸入1輸出的模糊推理系統(tǒng),其模糊規(guī)則可表述如下
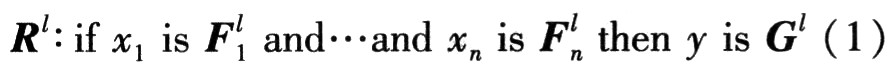
![]() 上的模糊集合,
上的模糊集合, 和y∈V對應(yīng)于系統(tǒng)輸入和輸出變量,l=1,2,…,M為模糊規(guī)則數(shù)。
和y∈V對應(yīng)于系統(tǒng)輸入和輸出變量,l=1,2,…,M為模糊規(guī)則數(shù)。
當(dāng)采用中心平均模糊消除器、乘積推理規(guī)則、高斯隸屬度函數(shù)和非單點模糊化時,得到的非單點模糊推理系統(tǒng)為
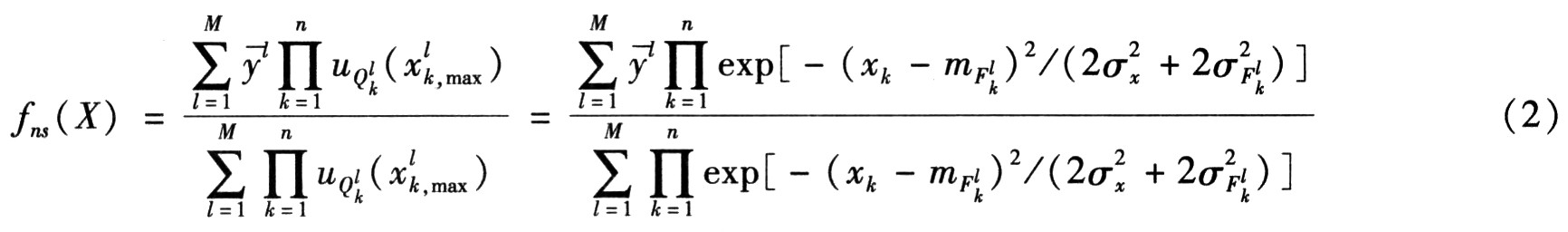
![]() 時,非單點模糊化與單點模糊化等價;當(dāng)輸入變量xk受到噪聲污染時,噪聲在非單點模糊器中會被因子
時,非單點模糊化與單點模糊化等價;當(dāng)輸入變量xk受到噪聲污染時,噪聲在非單點模糊器中會被因子![]() 所克服。如果σx≥σFkl,噪聲將會在很大程度上被抑制。
所克服。如果σx≥σFkl,噪聲將會在很大程度上被抑制。
2 NSFIS的參數(shù)學(xué)習(xí)算法
模糊推理系統(tǒng)是高度非線性系統(tǒng),在對復(fù)雜系統(tǒng)建模的過程中,其內(nèi)部參數(shù)![]() 主要依靠某種學(xué)習(xí)算法對輸入一輸出數(shù)據(jù)對進行訓(xùn)練來確定。目前,用于模糊推理系統(tǒng)的學(xué)習(xí)算法主要是梯度下降算法和遞推最小二乘算法。梯度下降算法簡單易行、運算量小,但收斂速度慢,容易陷入局部極值,且對信號的譜性依賴較大;遞推最小二乘算法收斂速度很快,對信號譜性無依賴,但其結(jié)構(gòu)復(fù)雜、運算量大且存在長期數(shù)值穩(wěn)定的問題。從工程的角度考慮,因為非單點模糊推理系統(tǒng)的計算復(fù)雜度本身就較大,所以運算量大的遞推最小二乘算法不適合采用。為了彌補梯度下降算法的缺點,文中引入遺傳算法。遺傳算法是模擬生物進化過程的一種全局優(yōu)化搜索算法,其目標(biāo)函數(shù)既不要求連續(xù),也不要求可微,僅要求問題可計算,而且它的搜索始終遍及整個解空間,容易得到全局最優(yōu)解。用梯度下降算法和遺傳算法同時并行的搜索解空間,并定期交換信息。這樣不僅避免了陷入局部極值的缺點,而且加快了收斂速度。雖然由于遺傳算法的加入,運算量增加了,但由于遺傳算法和梯度下降算法并行工作,所以沒有降低算法的實時性。采用減法聚類的方法設(shè)置初始參數(shù),進一步加快了算法的收斂速度。文中所設(shè)計的非單點模糊推理系統(tǒng)參數(shù)學(xué)習(xí)算法如下:
主要依靠某種學(xué)習(xí)算法對輸入一輸出數(shù)據(jù)對進行訓(xùn)練來確定。目前,用于模糊推理系統(tǒng)的學(xué)習(xí)算法主要是梯度下降算法和遞推最小二乘算法。梯度下降算法簡單易行、運算量小,但收斂速度慢,容易陷入局部極值,且對信號的譜性依賴較大;遞推最小二乘算法收斂速度很快,對信號譜性無依賴,但其結(jié)構(gòu)復(fù)雜、運算量大且存在長期數(shù)值穩(wěn)定的問題。從工程的角度考慮,因為非單點模糊推理系統(tǒng)的計算復(fù)雜度本身就較大,所以運算量大的遞推最小二乘算法不適合采用。為了彌補梯度下降算法的缺點,文中引入遺傳算法。遺傳算法是模擬生物進化過程的一種全局優(yōu)化搜索算法,其目標(biāo)函數(shù)既不要求連續(xù),也不要求可微,僅要求問題可計算,而且它的搜索始終遍及整個解空間,容易得到全局最優(yōu)解。用梯度下降算法和遺傳算法同時并行的搜索解空間,并定期交換信息。這樣不僅避免了陷入局部極值的缺點,而且加快了收斂速度。雖然由于遺傳算法的加入,運算量增加了,但由于遺傳算法和梯度下降算法并行工作,所以沒有降低算法的實時性。采用減法聚類的方法設(shè)置初始參數(shù),進一步加快了算法的收斂速度。文中所設(shè)計的非單點模糊推理系統(tǒng)參數(shù)學(xué)習(xí)算法如下:
步驟1:設(shè)置初始參數(shù)。采用減法聚類算法對訓(xùn)練數(shù)據(jù)[X,y]進行聚類處理,得M到個聚類中心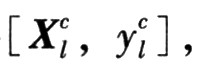 構(gòu)造非單點模糊系統(tǒng)初始參數(shù):選取聚類中心向量Xlc中的各個分量元素
構(gòu)造非單點模糊系統(tǒng)初始參數(shù):選取聚類中心向量Xlc中的各個分量元素![]() 作為式(2)中相應(yīng)
作為式(2)中相應(yīng)![]() 的初始值;以
的初始值;以![]() 與最近的另一個聚類中心歐式距離的一半
與最近的另一個聚類中心歐式距離的一半![]() 作為式(2)中
作為式(2)中![]() 作為式(2)中相應(yīng)的初始值;已知訓(xùn)練數(shù)據(jù)含有大量噪聲的情況下,取
作為式(2)中相應(yīng)的初始值;已知訓(xùn)練數(shù)據(jù)含有大量噪聲的情況下,取
步驟2:(1)采用梯度下降算法調(diào)整參數(shù)![]() (推導(dǎo)過程省略)。
(推導(dǎo)過程省略)。
(2)同時采用遺傳算法搜索最佳參數(shù)
1)對參數(shù)編碼。以減法聚類確定的初始參數(shù)值為參考,考慮參數(shù)的解空間在初始參數(shù)值的正負s倍范圍內(nèi),將解空間轉(zhuǎn)換為二進制,對各參數(shù)進行交叉組合編碼;
2)隨機生成20個個體作為初始群體;
3)將準(zhǔn)則函數(shù)的數(shù)學(xué)期望E[φ(e(t))]映射為適應(yīng)度函數(shù)
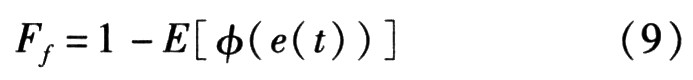
用該適應(yīng)度函數(shù)對群體中個體的適應(yīng)度進行評估,當(dāng)適應(yīng)度達到標(biāo)準(zhǔn)Ff,max時,進化停止;
4)遺傳操作:采用適應(yīng)度比例方法進行選擇,兩點交叉方法進行交叉,采用基本變異算子進行變異。
步驟3:梯度下降算法和遺傳算法之間的信息交換。遺傳算法每進化q代,根據(jù)準(zhǔn)則函數(shù)的數(shù)學(xué)期望E[φ(e(t))]比較遺傳算法和梯度下降算法所得參數(shù)的效果。若遺傳算法搜索到的參數(shù)更好,便用其作為梯度下降算法下一步運算的初始參數(shù);若梯度下降算法得到的參數(shù)更好,便用其替代遺傳算法的當(dāng)代群體中適應(yīng)度最差的一個個體。
步驟4:當(dāng)準(zhǔn)則函數(shù)的數(shù)學(xué)期望E[φ(e(t))]達到標(biāo)準(zhǔn)1-Ff,max時,或者遺傳算法進化g代時,算法停止。文中用準(zhǔn)則函數(shù)在訓(xùn)練數(shù)據(jù)時間長度內(nèi)的時間平均代替其數(shù)學(xué)期望進行運算。
3 基于NSFIS的制導(dǎo)炸彈智能控制系統(tǒng)的仿真設(shè)計
按照文獻[1]的設(shè)計思想,在仿真環(huán)境中采用NSFIS設(shè)計制導(dǎo)炸彈智能控制系統(tǒng)。
3.1 仿真環(huán)境的設(shè)定
假設(shè)以下的仿真環(huán)境:
(1)綜合風(fēng)速UZ方向在水平面內(nèi),且為常矢;
(2)重力加速度為9.8 m/s2,無阻尼;
(3)彈翼可產(chǎn)生的最大調(diào)控加速度max a(t)(max a(t)=maxax(t)+maxay(t))隨下落高度增加,且不考慮彈翼產(chǎn)生的加速度a(t)在鉛垂方向的分量;
(4)高度H為7 075.4 m(即下落時間T為38 s),按每0.25 s落下距離△h劃分高度空間為N=152層;
(5)轟炸方式為水平轟炸;
(6)控制過程不考慮時延;
(7)彈體運動為質(zhì)點運動。
3.2 炸彈運動方程的分析
根據(jù)文獻[9,10],水平轟炸的俯視圖,如圖1所示。
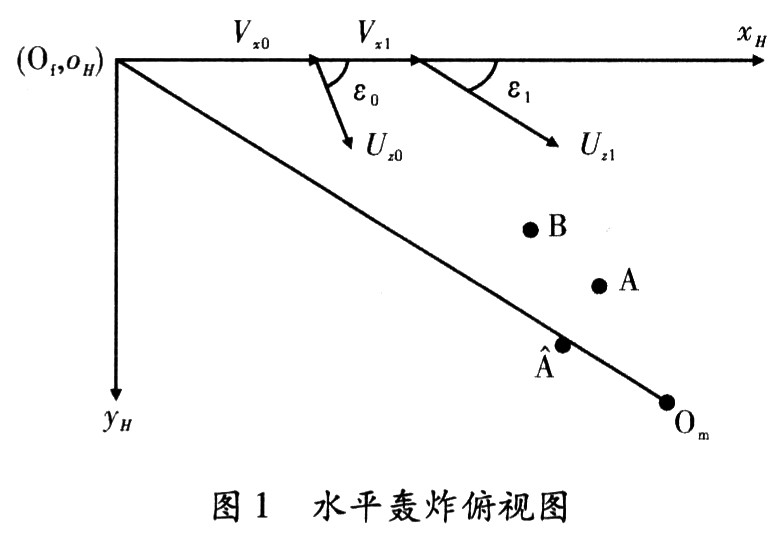
(oyxz)H:飛機航向坐標(biāo)系;Of:飛機投彈點;Om:地面目標(biāo);A:無需調(diào)控,可直接命中彈D0在t時刻的坐標(biāo)位置;A:需調(diào)控,方可命中彈D1在t時刻的坐標(biāo)位置;B:需調(diào)控,方可命中彈D1在t-1時刻的坐標(biāo)位置。
無需調(diào)控,可直接命中彈D0參數(shù):Vx0:投彈點飛機空速;Uz0:投彈D0時的綜合風(fēng)速;ε0:Vx0與Uz0的夾角;Xh(t):t時刻彈在xH方向的坐標(biāo)位置;Yh(t):t時刻彈在yH方向的坐標(biāo)位置。
需調(diào)控,方可命中彈D1參數(shù):Vx1:投彈點飛機空速;Uz1:投彈D1時的綜合風(fēng)速;ε1:Vx1與Uz1的夾角;Axe(t):t時刻和t-1時刻彈在xH方向的位移差;Aye(t):t時刻和t-1時刻彈在yH方向的位移差;Exh(t):t時刻彈與目標(biāo)Om的距離在xH方向的分量;Eyh(t):t時刻彈與目標(biāo)Om的距離在yH方向的分量;Vxh(t):t時刻彈的速度在xH方向的分量;Vyh(t):t時刻彈的速度在yH方向的分量。Axe(t):t時刻彈D1和彈D0的位移差在xH方向的分量;Aye(t):f時刻彈D1和彈D0的位移差在yH方向的分量。在仿真環(huán)境中,推導(dǎo)出彈D1在t時刻的運動方程
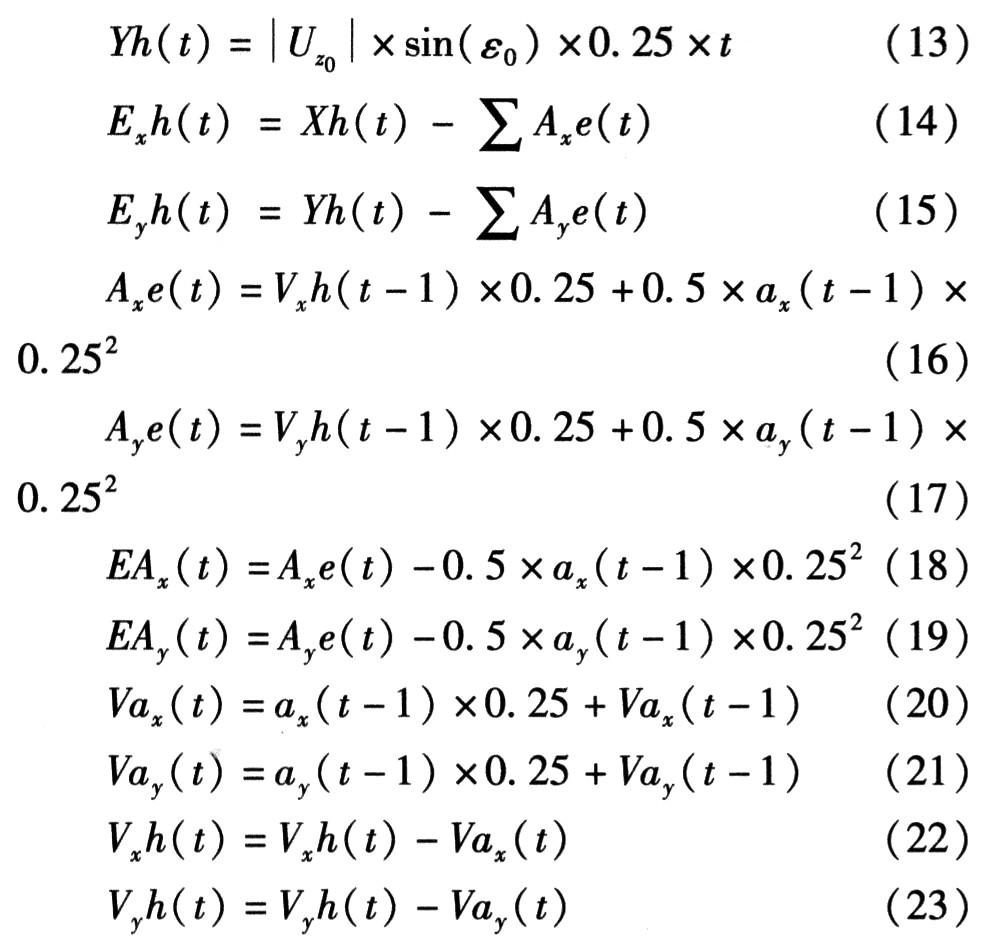
其中,Vax(t)為xH方向上t-1時刻加速度在時刻生成速度,Vay(t)為yH方向上t-1時刻加速度在t時刻生成速度。
3.3 制導(dǎo)炸彈智能控制系統(tǒng)的建立
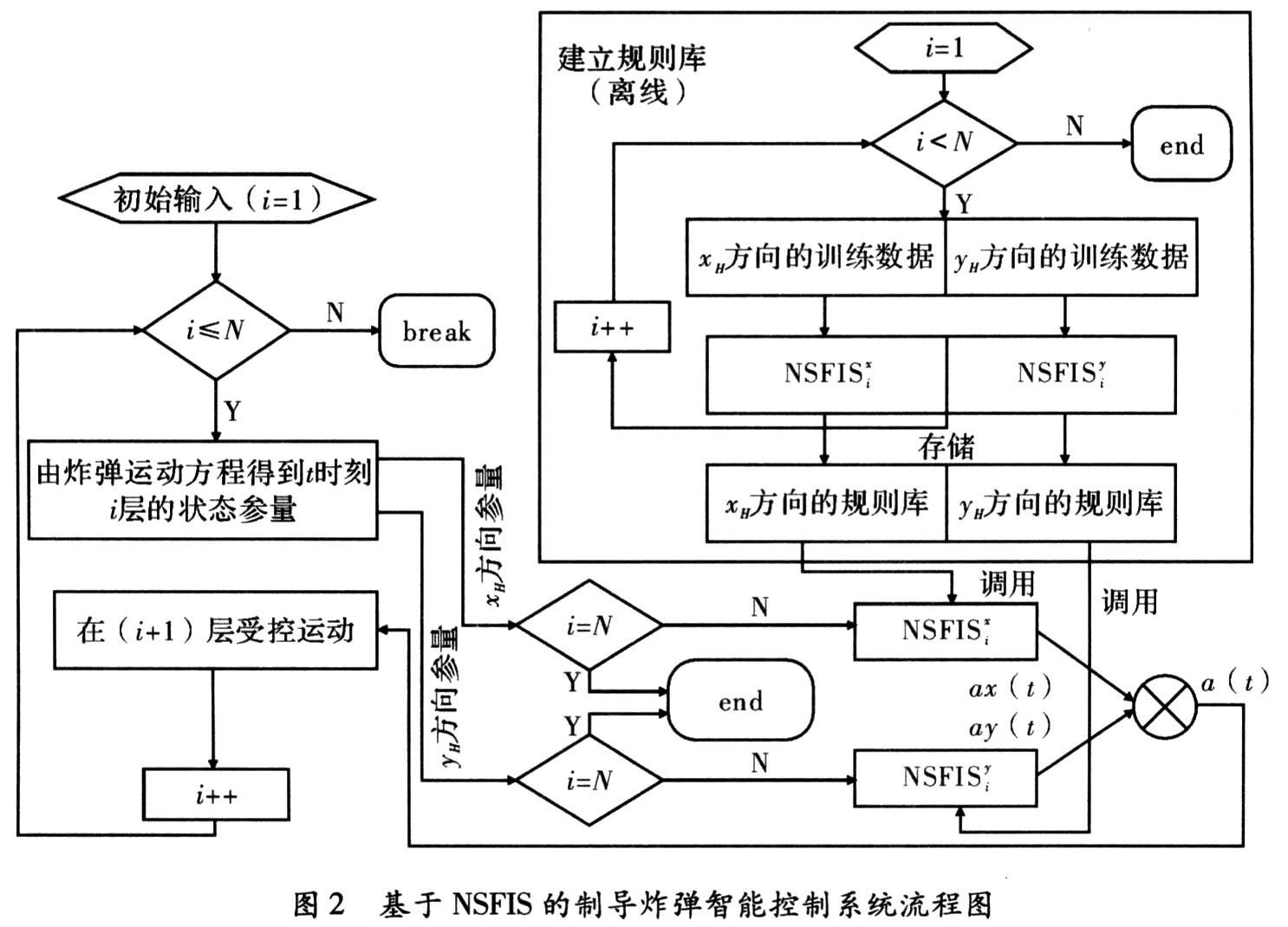
根據(jù)彈道運動方程,x與y方向的控制相互獨立(a(t)=ax(t)+ay(t)),所以對空間每一層建立兩個非單點模糊子系統(tǒng)(NSFISix和NSFISiy):NSFISix調(diào)控導(dǎo)彈在x方向的運動軌跡,輸入為Exh(t)、Axe(t)、Vxh(t),輸出為ax(t);NSFISiy調(diào)控導(dǎo)彈在y方向的運動軌跡,輸入為Eyh(t)、Aye(t)、Vyh(t),輸出為ay(t)。充分搜集每一層的訓(xùn)練數(shù)據(jù),利用文中提出的學(xué)習(xí)算法調(diào)整好NSFISix和NSFISiy的內(nèi)部參數(shù),就構(gòu)成了基于NSFIS的制導(dǎo)炸彈智能控制系統(tǒng),其概略流程圖,如圖2所示。
3.4 訓(xùn)練數(shù)據(jù)的獲取
首先,采用如下算式解算a(t)

弧度,|Uz1|=28、29、30、31 m/s,|Vx1|=319、320、321、322 m/s,ε1=0.3、0.4、0.5、0.6弧度;通過調(diào)節(jié)參數(shù)cx、cy,得到64組圓概率誤差CEP∈(4,5)m的訓(xùn)練數(shù)據(jù),并對其加入一定程度的擾動誤差。
3.5 檢驗
設(shè)兩種投彈初始條件:
(a)|Uz1|=30 m/s,|Vx1|=321 m/s,ε1=0.5弧度(經(jīng)訓(xùn)練的投彈初始條件,即教師知識);
(b)|Uz1|=30.8 m/s,|Vx1|=319.7 m/s,ε1=0.38弧度(未經(jīng)訓(xùn)練的投彈初始條件,即非教師知識)。
用含有擾動誤差的訓(xùn)練數(shù)據(jù),對基于ANFIS的制導(dǎo)炸彈智能控制系統(tǒng)和基于NSFIS的制導(dǎo)炸彈智能控制系統(tǒng)分別進行訓(xùn)練,并分別在(a)和(b)條件下進行投彈控制試驗。設(shè)得到兩種智能控制系統(tǒng)的控制結(jié)果比較如表1所示(表中數(shù)據(jù)為CEP,單位:m)。

從表1可以看出,無論在(a)還是(b)條件下,基于NSFIS的智能控制系統(tǒng)控制的命中精度都很高,而基于ANFIS的智能控制系統(tǒng)命中精度很低。這是因為ANFIS不具有抗噪聲能力,在訓(xùn)練的過程中,將擾動也作為經(jīng)驗進行了學(xué)習(xí),因此其推理誤差必然較大,控制不準(zhǔn)確。而NSFIS具有較強的抗噪聲能力,在學(xué)習(xí)過程中能夠去除擾動影響,因此其控制精度高。現(xiàn)實中,擾動是不可避免的,所以基于NSFIS的制導(dǎo)炸彈智能控制系統(tǒng)具有更高的工程應(yīng)用價值。
4 結(jié)束語
針對基于ANFIS的制導(dǎo)炸彈智能控制系統(tǒng)不具有抗噪聲能力的缺點,文中以非單點模糊推理系統(tǒng)為核心設(shè)計了一種新的制導(dǎo)炸彈智能控制系統(tǒng)。利用了非單點模糊推理系統(tǒng)的前置濾波特性,并提出用梯度下降算法和遺傳算法構(gòu)成的混合并行學(xué)習(xí)算法調(diào)整系統(tǒng)內(nèi)部參數(shù),解決了系統(tǒng)內(nèi)部參數(shù)動態(tài)自適應(yīng)調(diào)整的問題。試驗結(jié)果證明,在訓(xùn)練數(shù)據(jù)含有噪聲的情況下,基于NSFIS的制導(dǎo)炸彈智能控制系統(tǒng)能夠自動濾除噪聲,實現(xiàn)高精度控制。這對制導(dǎo)炸彈智能控制系統(tǒng)的工程實現(xiàn)具有一定的意義。

