摘  要： 通過對Apriori算法的研究和分析，結(jié)合算法存在的缺陷,，利用“桶”技術(shù)及壓縮組合項集技術(shù),，對頻繁項集提出了前綴概念,，并提出了基于前綴的頻繁項集挖掘算法,。該算法將具有同一前綴的頻繁項集的子集合作為一個節(jié)點，由頻繁k-項集的子集合直接產(chǎn)生候選(k+1)-項集,，從而省略了連接步中判斷I1,、I2是否能連接。同時,，該算法使得整個程序中節(jié)點數(shù)目減少,，這樣不僅減少了內(nèi)存消耗，而且提高了查找Ck和Lk的速度,，尤其便于大型數(shù)據(jù)庫的分布式處理,。經(jīng)實驗證實，改進后的算法是可行的,。
關(guān)鍵詞： Apriori算法,；關(guān)聯(lián)規(guī)則；頻繁項集,；“桶”技術(shù),；壓縮組合技術(shù)

    關(guān)聯(lián)規(guī)則挖掘概念最早由Agrawal等人在1993年提出[1]。1994年,，Agrawal等人建立了用于事務(wù)數(shù)據(jù)庫挖掘的項集格空間理論[2],，并提出了著名的Apriori算法，后其成為基本的關(guān)聯(lián)規(guī)則挖掘算法,。其核心原理是頻繁項集的子集是頻繁項集,，非頻繁項集的超集是非頻繁項集。
    關(guān)聯(lián)規(guī)則挖掘算法的設(shè)計可以分解為兩個子問題：
    (1)找到所有支持度大于最小支持度的項集(itemset),，稱之為頻繁項集(frequent itemset),；
    (2)由頻繁項集和最小可信度產(chǎn)生規(guī)則。
其中,，提高整個過程效率的關(guān)鍵在于提高問題(1)的效率,。針對問題(1)，本文對Apriori算法的實現(xiàn)提出了基于前綴的頻繁項集挖掘算法,。主要針對大型數(shù)據(jù)庫,，通過減少項集占用內(nèi)存和分段處理,，使設(shè)備資源在有限的情況下有效地實現(xiàn)頻繁項集挖掘。

1.2 相關(guān)關(guān)聯(lián)規(guī)則算法的評價
    由于Lk和Ck+1數(shù)目可能很大,，因此涉及的判斷和查找的計算量將會很大,；此外多次掃描事務(wù)數(shù)據(jù)庫，需要很大的I/O負(fù)載,；同時,，Lk和Ck+1占據(jù)的大量存儲空間中，有很大一部分是重復(fù)的,。
    針對Apriori算法的性能瓶頸,，許多的研究者在Apriori算法的基礎(chǔ)上提出了很多解決方法；同時,，也有許多研究者提出了非基于分層搜索的頻繁項集挖掘算法,。其中基于分層搜索的算法，主要從減少候選項集的規(guī)模并提高查找速度及掃描數(shù)據(jù)庫次數(shù)和規(guī)模兩方面考慮,。如Park基于散列技術(shù)和事務(wù)壓縮技術(shù)提出了DHP算法[4],，有效縮減了2候選項集的規(guī)模和掃描事務(wù)量，減少內(nèi)存消耗,，但此方法對大型數(shù)據(jù)庫如何合理地構(gòu)建Hash桶時比較難把握,。針對多次掃描數(shù)據(jù)庫的問題，有人提出了基于Tid表[5],、基于矩陣[6],、基于位陣[7]等的頻繁項集挖掘算法?；赥id表的頻繁項集挖掘算法利用得到L1后重組數(shù)據(jù)庫,，生成頻繁項集表，只需要2次訪問數(shù)據(jù)庫,?；诰仃嚒⑽魂嚨乃惴ㄊ抢镁仃噥泶鎯κ聞?wù)數(shù)據(jù)庫,，只需1次訪問數(shù)據(jù)庫,，同時利用矩陣、位陣的特性,，提高了運算速度,。無論是基于頻繁項集表，還是基于矩陣位陣的頻繁項集挖掘算法,，都需要占用大量內(nèi)存來一次性存儲頻繁項集表和事務(wù)數(shù)據(jù)庫,。此外，對于基于頻繁項集表的算法,，一個重組后規(guī)模為n的事務(wù),，根據(jù)排列組合原理將生成(2n-1)個規(guī)模大于1的子集,，再根據(jù)互補子集原理及棧原理，得出在最優(yōu)情況下時間復(fù)雜度為O(2n),，顯然生成頻繁項集表的時間消耗也不小,。因此，此類型算法不適于大型的事務(wù)數(shù)據(jù)庫,。
    在非基于分層搜索的算法中,，主要以FP_Growth[8]算法及其各種改進算法為主。這類算法,，需要2次訪問數(shù)據(jù)庫,。通過第1次訪問數(shù)據(jù)庫，得到L1,，并按支持度計數(shù)的遞減順序排序,，再采用“分治策略”構(gòu)造FP_Tree,，最后由FP_Tree挖掘出頻繁項集,。同基于矩陣的算法一樣，該算法需要大量內(nèi)存空間存儲FP_Tree,；此外,，刪除某一項時，對與此相關(guān)的節(jié)點支持度計算進行調(diào)整將花掉不少時間,，這主要是由于在Tree中只能由父節(jié)點直接查找子節(jié)點,，而不能由子節(jié)點查找父節(jié)點。因此,，對于大型數(shù)據(jù)庫,，此類算法也不適合。
    而對于Apriori算法,，可以考慮對每一輪的Lk重組項,，利用SQL優(yōu)化查詢訪問數(shù)據(jù)庫，來減少了每輪掃描的事務(wù)量及提高查找速度,，從而提高整體性能,。
2 改進的Apriori算法
    Apriori算法主要依賴于迭代性質(zhì)產(chǎn)生頻繁項集。候選(k+1)-項集ck+1的產(chǎn)生是在判斷頻繁k-項集I1,、I2能夠連接的基礎(chǔ)上產(chǎn)生的,。顯然，在按照單個頻繁項集為一個節(jié)點的情況下,，需要大部分時間來判斷I1,、I2是否能夠連接。如果頻繁項集不是很大,，則這個連接也不會花很多時間,；但若頻繁項集很大,，這個判斷過程將會花費很多時間。同時,，在計算候選項集計數(shù)時,，也將花費很多時間用于查找頻繁項集。
2.1 數(shù)據(jù)結(jié)構(gòu)
    Apriori算法數(shù)據(jù)結(jié)構(gòu)中的類主要包括以下幾種：
    (1)LkSet所有候選k-項集或頻繁k-項集集合,，關(guān)鍵屬性isets為LkISet集合,，Items為當(dāng)前Lk中所有的項集合，Iflags為對應(yīng)Items的簡約表示,，min最小支持度計數(shù),；
    (2)LkISet所有第一項相同的候選k-項集或頻繁k-項集集合，關(guān)鍵屬性first為項集的第一項,，nodes為LkNode集合,；
    (3)LkNode具有相同前綴(記為pres)的候選k-項集或頻繁k-項集集合。其中LkNode還有兩個關(guān)鍵的屬性,，一是rigths,，是節(jié)點中所有候選項集或頻繁項集的最后一項的集合體；二是degrees,是節(jié)點中所有候選項集或頻繁項集的計數(shù)的集合體,。
2.2 算法描述
    (1)初始條件：所有事務(wù)和項集都按照一定的原則對項進行排序,；掃描數(shù)據(jù)庫，產(chǎn)生L1,、Items和Iflags,，其中Items為當(dāng)前Lk中所有項的集合。
    (2)根據(jù)得到的L1,，由事務(wù)數(shù)據(jù)庫直接產(chǎn)生C2,，并對C2進行剪枝產(chǎn)生L2，同時更新Items和Iflags,。
    (3)由Lk連接產(chǎn)生Ck+1：CkfromLk(begin,end),。
    (4)掃描事務(wù)數(shù)據(jù)庫D，對Ck+1計數(shù)：Updatedegrees(D),；對任意d∈D：LkfromCk(d),。其中在Updatedegrees(D)中首先根據(jù)Items篩選有效地數(shù)據(jù)記錄，然后在根據(jù)事務(wù)的規(guī)模決定是否進入函數(shù)LkfromCk(),。
    (5)刪除計數(shù)小于min的ck+1：DeleteByMin-(begin),。
    (6)更新Items和Iflags：UpdateItems()。
    然后重復(fù)(3)～(6)步,，直到Lk=ø,。
    以下是一些函數(shù)的具體描述：
    (1)CkfromLk(begin,end)
    If(end<1) end=Lk.iset.size();
      For each iset in Lk.isets(begin...end)
      {  For each node in iset
        { If(node.rights>=2)
          { cnode.pres=node.presnode.rigths.get(j)；
             cnode.rigths=node.rigths(j+1...node.
            rigths.size()-1)；}//cnode∈Ck+1,；
        iset.remove(node); }
      isets.remove(iset); }
    由于大型數(shù)據(jù)庫的候選項集規(guī)模龐大,，若一次性得到所有候選項集，再進行剪枝,，可能會受到設(shè)備的限制,，因沒有足夠大的內(nèi)存而導(dǎo)致OutOfMemoryError。通過增加begin,、end參數(shù),，能夠有效地控制當(dāng)前候選項集的規(guī)模，不過這樣增加了計算支持度計數(shù)時訪問數(shù)據(jù)庫的次數(shù),。但是,，通過這些參數(shù)可以很方便地運用到分布式處理，能夠使各個塊互補干擾,，且所有塊的頻繁項集之和就為整個數(shù)據(jù)庫的頻繁項集,。在合成Ck+1的同時，刪除Lk中不需要的節(jié)點,。
    (2)LkfromCk(d)函數(shù)用來計算事務(wù)d對Ck計數(shù)的變化,。對?坌ck∈Ck，若ck?奐d,，則該項集支持度計數(shù)加1,。其具體表述為：
index=cnode.contain(d)；
if(cnode.presd) index=j+1,；
// d[j]=cnode.pres[k-1]
else index=-1；
if(index!=-1)
{  for each rights[i] in cnode.rights
    if(rights[i] in d[index...d.size()])
       cnode.degrees[i]++,； }
    (3)DeleteByMin(begin)函數(shù)用來修剪Ck,。其中參數(shù)begin用來控制iset的起始點。對于一次迭代,，需要分段處理時,，每一分段處理后得到的頻繁項集都屬于最終頻繁項集，與其他分段是互補干擾的,，因此begin用來確認(rèn)當(dāng)前分段的初始iset,，這樣使得這次的Updatedegrees(D)不會對前面分段產(chǎn)生影響，同時也提高了查找速度,。其具體表述為：
For each iset in this.iset[begin… size()]
{  For each node in iset
    {  For each degree[i] in node.degrees
       If(degree[i]<min)
       {  node.degrees.remove[i];
        node.rights.remove[i]; }
       If(node.Isempty()) iset.remove(node);}
    If(iset.Isempty()) this.iset.remove(iset)  }
3 實驗及性能分析
    本數(shù)據(jù)來源于http://grouplens.org網(wǎng)站,。首先預(yù)處理數(shù)據(jù)：select user,isbn from bxxbookratings where user in(select user from bxxusers) and isbn in(select isbn from bxxbooks)，最終得到記錄1 031 177條,，其中共有92 107個user和269 862種book,，事務(wù)的平均規(guī)模為11.2。
    運行環(huán)境：MyEclipse6.01；PC內(nèi)存：2GB,；繪圖環(huán)境：Matlab7.0,。
    
    由此可知，任何情況下,，改進后的Apriori算法內(nèi)存消耗都不可能多于改進前的Apriori算法內(nèi)存消耗,；且隨著事務(wù)數(shù)據(jù)庫越稠密，節(jié)點個數(shù)與項集個數(shù)差越大,，S越大,；此外，隨著k的增加,，S越大,，即改進后的算法空間占用越少。因此,，對比實驗主要針對時間消耗進行分析,。
3.1 對比實驗
    對于同一事物數(shù)據(jù)庫，頻繁項集挖掘的效率和結(jié)果主要取決于最小支持度閾值,；最小支持度閾值越大,，運行越快，得到的頻繁項集越少,。對于同一事物數(shù)據(jù)庫,，min越小，每次迭代產(chǎn)生的頻繁項集和候選項集越多,。圖1所示為對于同一事務(wù)數(shù)據(jù)庫,，隨min的不同，所需時間的對比情況,。
    對于規(guī)模相同,、稠密度不同的事務(wù)數(shù)據(jù)庫，在min相同時,，事務(wù)數(shù)據(jù)庫越稠密,，每次迭代產(chǎn)生的頻繁項集和候選項集越多。此種性質(zhì)類似于同一事務(wù)數(shù)據(jù)庫不同min時的性質(zhì),。因此,，對于不同稠密度事務(wù)數(shù)據(jù)庫的比較實驗，可以參照同一事物數(shù)據(jù)庫不同min的比較實驗,。由圖1可知,，事務(wù)數(shù)據(jù)庫越稠密，改進的Apriori算法優(yōu)勢越明顯,。表1給出了min=12時,，候選k-項集和頻繁k-項集的個數(shù)及其節(jié)點個數(shù)；圖2給出了min=12時，兩種算法在每次迭代中各個步驟所花時間的比較情況,。

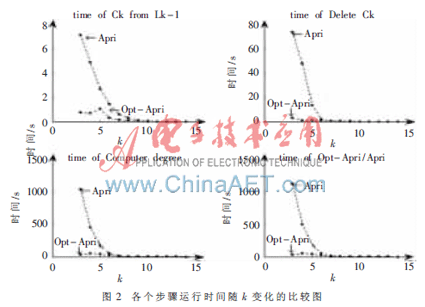
    根據(jù)算法自身的特點可知,，DeletebyMin()只需要一次遍歷所有候選項集的支持度計數(shù)；改進后的CkfromLk()只需要一次遍歷所有頻繁項集,，而非改進時,，還需要判斷兩個頻繁項集是否能連接，而存在某些頻繁項集多次訪問,；Updatedegrees()與事務(wù)相關(guān)聯(lián),，大量候選項集需要多次訪問。結(jié)合算法的特點,，從理論及實際上,，證明了總體運行時間主要取決于計數(shù)步，而隨著數(shù)據(jù)集越稠密,，改進后的算法優(yōu)勢更明顯,。
3.2 模擬分布式處理
    令min=12、k=4,，平均分為n段(n=1,，…，8)進行分段處理,，以模擬分布式處理,，得到結(jié)果如圖3所示。

    從圖3看出,，在一定誤差范圍內(nèi),，剪枝步和合成候選項集并沒有隨著n的變化而變化；計數(shù)所花時間隨著n的增加有細(xì)微的增加,；訪問數(shù)據(jù)庫所花時間隨著n的增加大而成倍數(shù)增加,；總體時間的變化主要取決于訪問數(shù)據(jù)庫所花時間。
      在深入研究Apriori算法及其相關(guān)算法的基礎(chǔ)上,，結(jié)合“桶”技術(shù)、壓縮組合原理,、數(shù)據(jù)重組等思想,，針對大型數(shù)據(jù)庫提出了基于前綴的頻繁項集挖掘算法，并且根據(jù)實際情況,，對頻繁k-項集的產(chǎn)生采用了直接從數(shù)據(jù)庫得出的,、有別與其他頻繁項集產(chǎn)生的特殊處理方法。理論和實驗表明,，改進后的Apriori算法在時間和空間上都有改進,，且能夠進行分段處理并運行到分布式處理中。在用于分段處理時，如何確定有分段使運行效果最優(yōu),，還有待進一步研究,。
參考文獻(xiàn)
[1] AGRAWAL R,IMIELINSKI T,SWAMI A. Database mining:a performance perspective[J]. IEEE Transactions on Knowledge and Data  Engineering,1993,5(6):914-925.
[2] AGRAWAL R,SRIKANT R.Fast algorithms for  mining association rules in large databases[C]. In Proc.Of the 20th Int.Conf.on Very Large Data Bases(VLDB),Santiago,Chile,Septemer，1994(2):478-499.
[3] HAN Jiawei,MICHELINE K.數(shù)據(jù)挖掘概念與技術(shù)[M].北京：機械工業(yè)出版社,2006.
[4] PARK J S,CHEN M S,YU P S.Using a hashbased method with transaction trimming for mining association rules[J].IEEE Trans on  Knowledges Data Engineering,1997,9(5):813-825.
[5] 向程冠,姜季春,陳梅,等.AprioriTid算法的改進[J].計算機工程與設(shè)計,2009,，30(15):3581-3583.
[6] 胡斌,蔣外文,蔡國民,等.基于位陣的更新最大頻繁項集算法[J].計算機工程,2007,28(2):59-61.
[7] 王鋒,李勇華,毋國慶.基于矩陣的改進的Apriori算法[J].計算機工程與設(shè)計,2009,，30(10):2435-2438.
[8] Liu Yongmei,Guan Yong.FP_growth algorithm for application in research of market basket analysis[J].Computational Cybernetics,2008.ICCC 2008.IEEE International Conference on,2008: 269-272.