引　　言

　　1946年,，第一臺(tái)電子計(jì)算機(jī)的誕生開創(chuàng)了計(jì)算機(jī)發(fā)展的新紀(jì)元。隨著計(jì)算機(jī)科學(xué)技術(shù)的迅速發(fā)展,，計(jì)算機(jī)的應(yīng)用領(lǐng)域越來越廣泛,，并逐漸形成科學(xué)發(fā)展中的一個(gè)新的分支。在計(jì)算機(jī)的主要工作中,，處理大量的數(shù)據(jù)是其一項(xiàng)基本功能,；因而數(shù)據(jù)運(yùn)算是必不可少的。于是人們?cè)O(shè)法在硬件設(shè)計(jì)與數(shù)據(jù)結(jié)構(gòu)方面努力進(jìn)行工作［1］,，使計(jì)算機(jī)的速度不斷提高,。

　　十幾年前，單片微型機(jī)脫穎而出,，逐漸應(yīng)用于微型計(jì)算機(jī)的各個(gè)領(lǐng)域,，它不僅適用于一般的自動(dòng)控　　制，而且還可以承擔(dān)高精度的數(shù)據(jù)處理工作,。誠然,，在許多系統(tǒng)中近來采用DSP來提高微機(jī)的數(shù)據(jù)處理能力，以便完成復(fù)雜的圖像處理,、音頻處理,、網(wǎng)絡(luò)通訊等功能，而且是一個(gè)趨勢(shì),；但在這些系統(tǒng)中仍不可忽視運(yùn)算程序的執(zhí)行速度,，因?yàn)楹玫乃惴梢源蟠筇岣叱绦虻膱?zhí)行效率［2］。同時(shí),，考慮到目前8BITMCU的主導(dǎo)地位及某些系統(tǒng)不適合配置DSP來進(jìn)行數(shù)據(jù)處理［3］,。因此,，這里仍有必要對(duì)高精度高速度的浮點(diǎn)多字節(jié)運(yùn)算進(jìn)行進(jìn)一步研究。

　　1　浮點(diǎn)多字節(jié)標(biāo)準(zhǔn)乘法

　　普通的計(jì)算機(jī)都采用標(biāo)準(zhǔn)的加法－移位技術(shù)來實(shí)現(xiàn)乘法,，Mowle曾經(jīng)對(duì)這些基本的乘法算法和問題作了詳細(xì)的描述［4］。對(duì)于二進(jìn)制數(shù)A,，B來說,，設(shè)其數(shù)值為AV，BV

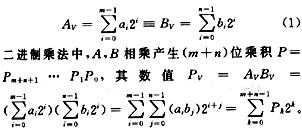
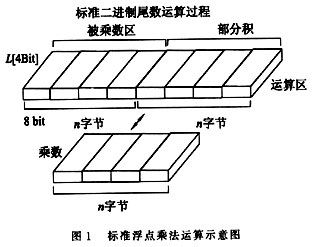
　　由此原始矩陣乘法產(chǎn)生了標(biāo)準(zhǔn)的移位加算法［5,，6］,。一般的標(biāo)準(zhǔn)浮點(diǎn)乘法運(yùn)算分為階碼運(yùn)算與尾數(shù)運(yùn)算兩部分，其主要部分為尾數(shù)運(yùn)算,。標(biāo)準(zhǔn)尾數(shù)相乘是采用邊乘邊相加的辦法（即加法－移位）來實(shí)現(xiàn)的,，即乘數(shù)向左移位，產(chǎn)生中間結(jié)果,，中間結(jié)果被加至積區(qū)的方法,；在整個(gè)過程中，積也與乘數(shù)一起移位,。此過程如圖1所示,。上述方法對(duì)于兩個(gè)n位二進(jìn)制尾數(shù)的相乘結(jié)果，即乘積為2n位,，也就是部分積要點(diǎn)n位,，在運(yùn)算過程中，這2n字節(jié)都有可能要有相加的操作,，需2n個(gè)字節(jié)加法器,。對(duì)于標(biāo)準(zhǔn)算法，相當(dāng)于進(jìn)行了8n次2n字節(jié)的移位,，還有次2n字節(jié)的加法,。其中Pj（bj）為其每個(gè)bit位的布爾取值，其為1則取1,，反之則為0,。

　　為了節(jié)省運(yùn)算時(shí)間，標(biāo)準(zhǔn)乘法應(yīng)用標(biāo)準(zhǔn)右移乘法方法以便減少加法器的數(shù)量,，有關(guān)這方面的具體論述請(qǐng)參見文［2］,。

　　2　掃描乘法的基本原理

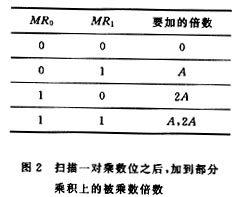
　　在執(zhí)行乘法指令時(shí)，如果每個(gè)周期所檢查的乘數(shù)位多于一位,，乘法的速度便可以加快,。例如，每次檢查二位,，那么加法移位周期的總數(shù)就可以減半,。這些逐次掃描的位組可以是分離的,，也可以是重疊的。這里先簡述一下分離掃描的原理,。對(duì)于乘數(shù)來講是以字節(jié)為單位的,，其字長按二進(jìn)制BIT來計(jì)是偶數(shù)，設(shè)被乘數(shù)A＝（AX）,，乘數(shù)B＝（MR）,；則在掃描了最低一對(duì)乘數(shù)位（MR1，MR0）后,，有四種可能的動(dòng)作,，如圖2所示。對(duì)于m＝（MR1,，MR0）2來說,，被乘數(shù)A的倍數(shù)m×A被加到當(dāng)前的部分乘積上，用來生成下一個(gè)部分積,。上述原理可以推廣到任意大小的掃描位組,，其具體實(shí)現(xiàn)方法和分析結(jié)果請(qǐng)參見文［2］，這里不再敘述,。

　　以上所描述的是分離掃描的情況,，下面再介紹重疊多位掃描的情況。一般在乘數(shù)中bj為0的個(gè)數(shù)越多,，則程序運(yùn)行的時(shí)候?qū)?的情況僅僅是移位越過,，而不用作加法的運(yùn)算，在此種情況下的運(yùn)算相對(duì)加快,。因此希望對(duì)乘數(shù)的bj能否進(jìn)行適當(dāng)?shù)牟僮?，使這之在bj為1的區(qū)域也能使運(yùn)算時(shí)間減少。

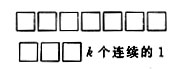
　　現(xiàn)考慮乘數(shù)中有一串k個(gè)連續(xù)的1,，如下

　　列的位置…,，i＋k，i＋k－1,，i＋k－2,，…，i,，i－1,，…

　　列的內(nèi)容…，0,，1,，1，…，1,，0,，… （2）

　　按常規(guī)，在移位加時(shí),，被乘數(shù)A與部分積要進(jìn)行k次加法操作,，但是存在

　　2i＋k－2i＝2i＋k－1＋2i＋k－2＋…＋2i＋1＋2i　 （3）

　　因此可以用下面的數(shù)符串來代替k個(gè)連續(xù)的1

　　列的位置…，i＋k,，i＋k－1,，i＋k－2，…,，i，i－1,，…

　　列的內(nèi)容…,，1，0,，0,，…，－1,，0,，… （4）

　　上面的－1表示執(zhí)行一次減法。利用這種乘法再編碼的方法,，只要在數(shù)字串開始時(shí)作一次加法,，結(jié)束時(shí)作一次減法，使這能夠代替原來的k次連續(xù)加法,。顯然,，當(dāng)k很大時(shí)，能節(jié)省大量的加法時(shí)間,。

　　為了方便掃描,，乘數(shù)位仍按二位一組分成許多組，但一次掃描三位,，二位來自現(xiàn)在的組,，第三位來自下一次高次組的低位，實(shí)際上每一組的低位被檢測(cè)了二次,。為了與右移算法取得一致,，假定掃描乘數(shù)從右端到左端，重疊和非重疊兩種掃描模式表示見圖3,。

　　設(shè)掃描組XR＝［Xi＋1,，Xi］2；下一掃描組XR′＝［Xi＋3,，Xi＋2］2,；每三位一組檢測(cè)后的動(dòng)作說明見圖4,。其指出了每個(gè)機(jī)器周期或執(zhí)行一次單純的移位，或者執(zhí)行一次加法,，或者執(zhí)行一次減法,，這里只需要倍數(shù)2A或4A。當(dāng)下一對(duì)的低次位xi＋2為0時(shí),，三位中最左邊的1經(jīng)常指示一串1的左端（結(jié)束）,。依式（3）所描述的特性，在具有非零的乘數(shù)位時(shí)應(yīng)該執(zhí)行加法,。另一方面,，當(dāng)xi＋2＝1 時(shí)，即意味著是一串1的右端（開始）或中心,，按照串特性需要作一次減法,，在每個(gè)加法周期中，部分乘積每次要右移二位,。這就使部分乘積比它應(yīng)該具有的數(shù)值少了4倍被乘數(shù)（－4A）,。這可以用在下一步掃描中加上所需被乘數(shù)的倍數(shù)與4倍數(shù)的差值來校正。倍數(shù)2A或4A進(jìn)入加法器的地點(diǎn)是重要的,。如果一對(duì)的尾數(shù)是 0,，那么所得到的部分乘積是正確的，而且下一次的操作是一次加法,。如果一對(duì)的結(jié)尾是1,，則所得到的部分乘積太大，所以下一次操作將是一次減法,。

　　3　單片機(jī)重疊掃描乘法運(yùn)算的實(shí)現(xiàn)

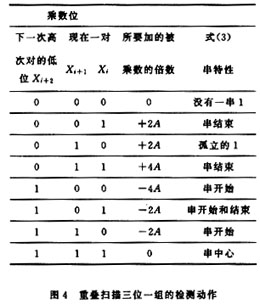
　　從以上原理可知,，針對(duì)二位一組的情況需要五個(gè)被乘數(shù)的倍數(shù)，其數(shù)值可取為0,，±2A,，±4A。由于其每移二位至多操作一次加減法,，在多字節(jié)的運(yùn)算中對(duì)提高執(zhí)行效率有很大的益處,；不過考慮到8BITMCU的移位操作并沒有二位一移的指令，對(duì)這種掃描算法有很大的障礙,，必須重新考慮掃描運(yùn)算如何在微型機(jī)上進(jìn)行實(shí)施,。

　　根據(jù)文［2］，MCU對(duì)字節(jié)與半字節(jié)操作的指令較強(qiáng),，因此可以在掃描算法的基礎(chǔ)上擴(kuò)展其掃描位組,，這樣在每個(gè)加法周期中的運(yùn)算變得很復(fù)雜，因此首先必須研究清楚這種情況。

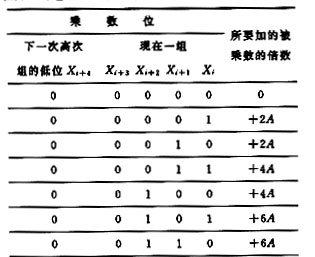
　　將乘數(shù)位按4BIT分成一組,，一次掃描五位,；設(shè)本組為BMi＝［Xi＋3，Xi＋2,，Xi＋1,，Xi］，下一次要掃描的BMi′的低位為Xi＋4,；這樣在掃描過程中的情況與文［3］所介紹的情況有類似之處,，但這里進(jìn)行運(yùn)算的次數(shù)不但與BMi有關(guān)，同時(shí)下一次掃描的低位對(duì)本算法也有重大的影響作用,。假定在運(yùn)算數(shù)中0,，1的概率出現(xiàn)機(jī)會(huì)均等，對(duì)4位一組的掃描進(jìn)行分析,?！　「鶕?jù)重疊掃描算法的原理，BMi′低位為0時(shí)（如圖5所示）,，組中最左端的1指示一串1的左端（結(jié)束）。依據(jù)式（3）,，很容易得到每次掃描部分積所要加的被乘數(shù)倍數(shù)（見圖5）,，可以得到其倍數(shù)，即相加的倍數(shù)

　　Pj＝｛BMi－2G［BMi／2］｝A＋BMi．A　?。?（BMi－G［BMi／2］）A （5）

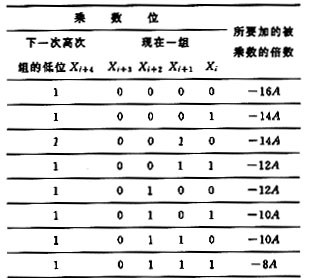
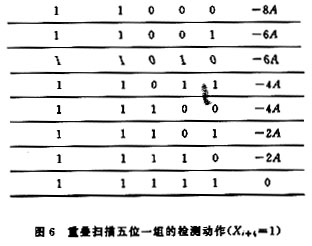
　　其中G［］為取整函數(shù),。Pj實(shí)質(zhì)上均與2A有關(guān)，這一點(diǎn)從圖中可以看到,。如果一組的結(jié)尾是零,，那么所得到部分乘積是正確的，按正常操作,；如果一組的結(jié)尾是1,，那么所得的部分積同上一次掃描有關(guān)；所以此時(shí)只是在掃描第一組時(shí)做一下記錄,，在最后完成時(shí)針對(duì)它在最尾端減一次A即可,。這一點(diǎn)對(duì)于BMi′低位為1時(shí)也成立。其部分積加的情況如圖6所示,。

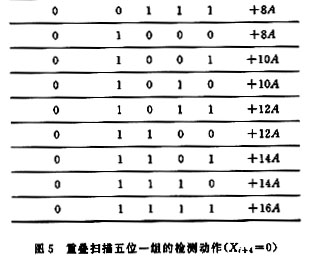
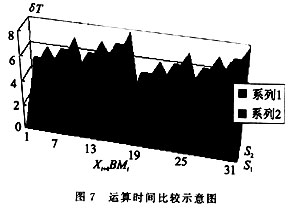
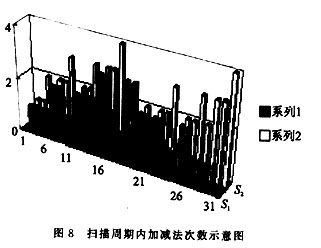
　　區(qū)別只是改加為減,，因?yàn)椴糠址e的減值在以后的掃描中可以修正回來，不用采用補(bǔ)碼的運(yùn)算也能完成,，最常用的方法是設(shè)置輔助運(yùn)算區(qū),，采用臨時(shí)記錄的方式保證其部分積在掃描任一周期保持正確結(jié)果，也稱為臨時(shí)擴(kuò)展方法，這里就不重復(fù),。這樣,，在每次掃描僅剩下一個(gè)問題，即如何處理Pj,，這里Pj與文［3］中處理的方法有類似之處,。以2A為基礎(chǔ)，將Pj形成一個(gè)加（減）法序列,，也就是將Pj變?yōu)?qA的序列,，如12A＝22A＋23A。這樣就可以在一個(gè)掃描周期完成部分積的加法,。這里建議讀者去探索Pj更好的形成方法,，因?yàn)樾纬?qA的序列，1≤q≤3,，要占用時(shí)間（24A可以通過半字節(jié)操作做左端拼加處理,，因?yàn)?4A相當(dāng)于A左移半字節(jié)，運(yùn)算時(shí)直接依靠輔助運(yùn)算區(qū)）,，同時(shí)在特殊處理上也額外占有一些運(yùn)算時(shí)間,，這一點(diǎn)在圖7中也可以看出來。這樣一來,，在Pj的加法過程中,，掃描算法在某些BMi值上并不都占優(yōu)勢(shì)，這一點(diǎn)在圖5,，6中也可以體現(xiàn)（BMi中Xi＋3,，Xi＋2，Xi＋1,，Xi為1的個(gè)數(shù)決定了在標(biāo)準(zhǔn)算法中的加法次數(shù)）,；但重疊掃描畢竟節(jié)省了時(shí)間，其與標(biāo)準(zhǔn)算法在一個(gè)掃描周期內(nèi)的加法次數(shù)情況如圖8所示（其中系列1為重疊掃描算法,，系列2為標(biāo)準(zhǔn)算法）,。加之在移位中節(jié)省的時(shí)間，重疊掃描全過程的運(yùn)算時(shí)間與標(biāo)準(zhǔn)右移算法的比較情況如圖8所示（S1為重疊掃描算法,，S2為標(biāo)準(zhǔn)算法）,。在局部區(qū)域，由于采用上述的Pj處理方法,，運(yùn)算時(shí)間節(jié)省情況還不甚理想,，但在總體上還是有很大的改進(jìn)。

　　4　結(jié)　　論

　　以上介紹的是重疊均勻移位掃描算法,，前面談到重疊非均勻移位掃描算法,，有關(guān)這種算法的詳細(xì)介紹請(qǐng)參見其他文獻(xiàn),。

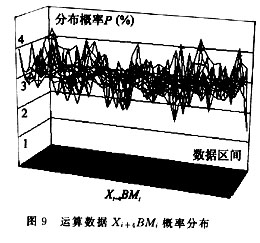
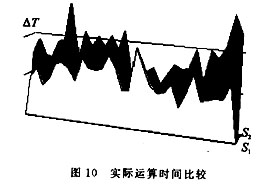
　　在以上過程中，是假定BMi中的Xi＋3,，Xi＋2,，Xi＋1，Xi值的1,，0分布服從自然概率,，然而在運(yùn)算中由于Xi＋4的作用，在對(duì)某區(qū)間數(shù)據(jù)進(jìn)行操作時(shí)存在差異,，通過對(duì)一些運(yùn)算區(qū)間的數(shù)據(jù)進(jìn)行了統(tǒng)計(jì),，其Xi＋4與BMi值的分布概率如圖9所示；以實(shí)際的一組分布來驗(yàn)證重疊算法運(yùn)算時(shí)間的縮短情況,，如圖10所示（S1為重疊掃描算法,，S2為標(biāo)準(zhǔn)算法；圖中前面為S1,，后面陰影為S2）,。可以看到重疊掃描法對(duì)浮點(diǎn)多字節(jié)乘法運(yùn)算有很大的改進(jìn),，它打破了移位加法的傳統(tǒng)乘法算法,，有了算法的預(yù)測(cè)功能，提高了乘法運(yùn)算的速度,。本算法在某軍工項(xiàng)目中得到應(yīng)用,，效果很好。

　　參考文獻(xiàn)

　　1　黃　凱．計(jì)算機(jī)算術(shù)運(yùn)算原理,、結(jié)構(gòu)與設(shè)計(jì)．北京：科學(xué)出版社，1980．106～110

　　2　陳　宇,，王遵立．MC－51單片微型機(jī)上實(shí)現(xiàn)的快速掃描浮點(diǎn)乘法運(yùn)算．?dāng)?shù)據(jù)采集與處理,，1992，（9）：151～153

　　3　陳　宇,，畢淑艷,，王遵立，等．MCS－51單片機(jī)實(shí)現(xiàn)的快速浮點(diǎn)多字節(jié)BCD乘除運(yùn)算．電子技術(shù)應(yīng)用,，1998,，（2）：17～19

　　4　Chen T C．A binary multiplication scheme based onsquaring．IEEE Trans Comput，1971,，C－20（6）：678～680

　　5　Booth A D．A signed binary multiplication technique．Quart Journ Mech and Appl,，Math，1951,，4（2）：236～240

　　6　Garner H L．A ring model for the study for a binarymultiplier using 2，3 or 4－bit at a time．IEEE Trans,，1959,，EC－80（1）：25～30