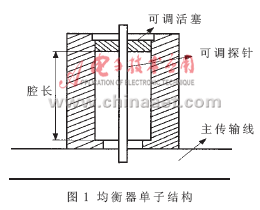
但由于單子結(jié)構(gòu)帶寬和吸收衰減幅度的有限性,，為了能在較寬頻帶內(nèi)實(shí)現(xiàn)對大功率微波管的高精度均衡，必須采用多級子結(jié)構(gòu)級聯(lián)的形式,。所以在工程實(shí)踐中,，針對均衡器的復(fù)雜特性提出了以海量數(shù)據(jù)庫為基礎(chǔ)的網(wǎng)絡(luò)子結(jié)構(gòu)互聯(lián)分析方法。在數(shù)據(jù)庫的建立過程中,，利用網(wǎng)絡(luò)分析儀對均衡器單腔子結(jié)構(gòu)進(jìn)行S參數(shù)的測量，建立相應(yīng)的S參數(shù)測量數(shù)據(jù)庫,。此數(shù)據(jù)庫中每個測量點(diǎn)對應(yīng)的均衡器物理參數(shù)為：諧振腔的腔長L_c,，耦合探針插入傳輸線深度L_s，介質(zhì)微擾插入諧振腔深度La,。由工程實(shí)踐可知,，三個物理參數(shù)對諧振頻率點(diǎn)的頻率影響是有規(guī)律可循的。通常,，諧振頻率隨Lc的增大而降低,；諧振頻率隨Ls的增大而降低，同時衰減增大,；諧振頻率隨La的增大而降低,，同時衰減減小。
2 神經(jīng)網(wǎng)絡(luò)模型設(shè)計
2.1 RBF神經(jīng)網(wǎng)絡(luò)
　　RBF（Radius Base Function）是最近十年興起的一種新型的神經(jīng)網(wǎng)絡(luò),，它具有網(wǎng)絡(luò)結(jié)構(gòu)簡單,、網(wǎng)絡(luò)訓(xùn)練速度快（與BP算法相比，RBF網(wǎng)絡(luò)的訓(xùn)練算法可以快一個數(shù)量級）,、仿真精度高等優(yōu)點(diǎn),。RBF網(wǎng)絡(luò)同時具有良好的局部性，能提供平滑,、性能優(yōu)秀的離散數(shù)據(jù)內(nèi)插特性,，由該網(wǎng)絡(luò)構(gòu)成的系統(tǒng)是有界、穩(wěn)定的,。
　　RBF神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)如圖2所示,，它是一種兩層網(wǎng)絡(luò)，第一層由RBF神經(jīng)元作為隱神經(jīng)元（傳輸函數(shù)為高斯函數(shù)）,，圖中a_1i的表示向量a₁的第i個元素,；b_1i表示向量b₁的第i個元素(即第i個RBF神經(jīng)元的方差)；i_W1表示矩陣W₁的第i行,，即第i個神經(jīng)元的中心,。第二層由線性神經(jīng)元(傳輸函數(shù)為線性函數(shù))作為輸出神經(jīng)元。其中S₁,、S₂分別表示第一層和第二層神經(jīng)元的數(shù)目,。

　　若考慮S2=1的情況,，此時把整個神經(jīng)網(wǎng)絡(luò)看成一個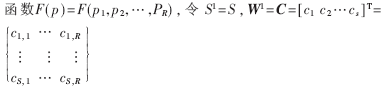

其中,c_i(i=1,2,…,S)為矩陣C的每一行，它代表相應(yīng)神經(jīng)元徑向基函數(shù)的中心向量,，b₁₌λ=(λ₁,λ₂,，…λ_S),其中λ_i代表徑向基函數(shù)的方差，W₂=W=(w₁,w₂,…,w_S),，則網(wǎng)路輸出為：
???
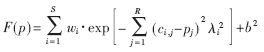
2.2 網(wǎng)絡(luò)的訓(xùn)練
　　僅僅搭建這樣一個模型是沒有意義的,，神經(jīng)網(wǎng)絡(luò)在實(shí)際工作之前必須進(jìn)行學(xué)習(xí)，通過學(xué)習(xí),，神經(jīng)網(wǎng)絡(luò)才能獲得一定的“智能”,。
　　學(xué)習(xí)是神經(jīng)網(wǎng)絡(luò)一種最重要也最令人矚目的特點(diǎn)。在神經(jīng)網(wǎng)絡(luò)的發(fā)展進(jìn)程中,，學(xué)習(xí)算法的研究有著十分重要的地位,。目前，人們所提出的神經(jīng)網(wǎng)絡(luò)模型都是與學(xué)習(xí)算法相對應(yīng)的,。所以,，有時人們并不苛求對模型和算法進(jìn)行嚴(yán)格的定義或區(qū)分。有的模型可以有多種算法,，而有的算法可能用于多種模型,。
　　本文根據(jù)均衡器的傳輸特性，在訓(xùn)練學(xué)習(xí)過程中,，其連接權(quán)值的不斷調(diào)整以及學(xué)習(xí)修正采用BP網(wǎng)絡(luò)學(xué)習(xí)算法中的LM算法,。LM算法是為了訓(xùn)練中等規(guī)模的前饋神經(jīng)網(wǎng)絡(luò)而提出的最快速算法，它對MATLAB實(shí)現(xiàn)也是相當(dāng)有效的,，在BP網(wǎng)絡(luò)的眾多學(xué)習(xí)算法中,，通常對于包含數(shù)百個權(quán)值的函數(shù)逼近網(wǎng)絡(luò)，LM算法的收斂速度最快,。如果要求的精度比較高,，則該算法的優(yōu)點(diǎn)尤其突出。在許多情況下,，采用LM算法的訓(xùn)練函數(shù)trainlm可以獲得比其他算法更小的均方誤差,。
LM算法實(shí)際上是梯度下降法和牛頓法的結(jié)合。梯度下降法在開始的幾步下降較快,，當(dāng)接近最優(yōu)值時,，由于梯度趨于零，使得目標(biāo)函數(shù)下降緩慢,；而牛頓法可以在最優(yōu)值附近產(chǎn)生一個理想的搜索方向,。其主要算法為:
　　

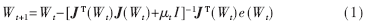
　　其中J是包含網(wǎng)絡(luò)誤差對權(quán)值及閾值的一階導(dǎo)數(shù)的雅可比矩陣。

　　牛頓法能夠更快更準(zhǔn)確地逼近一個最小誤差,，在每一步成功后,，μ都會減小,，只有當(dāng)發(fā)現(xiàn)下一步輸出變壞時才增加μ。按這種方法,，算法的每一步運(yùn)行都會使目標(biāo)函數(shù)向好的方向發(fā)展,。
　　算法開始時，μ取小值μ=0.001,。如果某一步不能減小E,，則將μ乘以10后再重復(fù)這步，最后使E下降,。如果某一步產(chǎn)生了更小的E,，則將μ乘以0.1繼續(xù)運(yùn)行。算法的執(zhí)行步驟如圖3所示,。

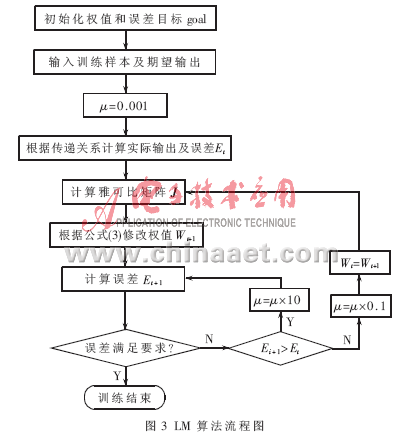
　　對于RBF網(wǎng)絡(luò)與BP網(wǎng)絡(luò)的主要區(qū)別在于使用不同的作用函數(shù),，BP網(wǎng)絡(luò)中的隱層節(jié)點(diǎn)使用的是Sigmoid函數(shù),，其函數(shù)值在輸入空間中無限大的范圍內(nèi)為非零值,。而RBF網(wǎng)絡(luò)的作用函數(shù)為高斯函數(shù)，因而其對任意的輸入均有高斯函數(shù)值大于零的特性,，從而失去調(diào)整權(quán)值的優(yōu)點(diǎn),。但加入LM算法進(jìn)行網(wǎng)絡(luò)訓(xùn)練后，RBF網(wǎng)絡(luò)也同樣具備局部逼近網(wǎng)絡(luò)學(xué)習(xí)收斂快的優(yōu)點(diǎn),，可在一定程度上克服高斯函數(shù)不具備緊密性的缺點(diǎn),。由于RBF網(wǎng)絡(luò)采用高斯函數(shù)，表示形式簡單,，即使對于多變量輸入也不增加太多的復(fù)雜性,。
2.3 仿真設(shè)計結(jié)果
　　在建模過程中，如果要建立精確的神經(jīng)網(wǎng)絡(luò)模型,，通常需要提供大量的訓(xùn)練樣本,。而在課題開展過程中，針對微波均衡器的復(fù)雜特性提出了以海量數(shù)據(jù)庫為基礎(chǔ)的網(wǎng)絡(luò)子結(jié)構(gòu)互聯(lián)分析方法,。這一方法的提出為建立均衡器神經(jīng)網(wǎng)絡(luò)模型提供了大量準(zhǔn)確的訓(xùn)練樣本,。
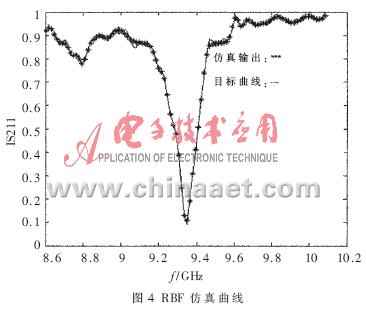
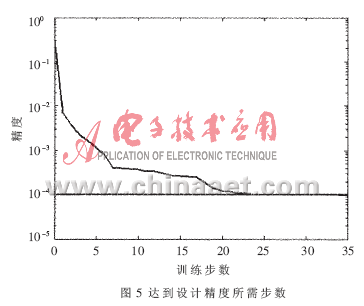
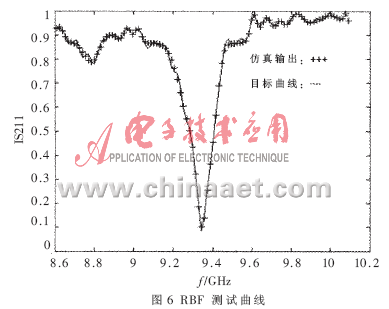
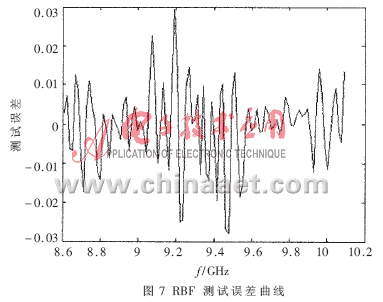
　　文中采用加入LM算法進(jìn)行網(wǎng)絡(luò)訓(xùn)練的RBF網(wǎng)絡(luò)對均衡器進(jìn)行建模，將均衡器的結(jié)構(gòu)尺寸（諧振腔的腔長,、探針插入主傳輸線的深度,、吸收材料插入深度）和頻率作為神經(jīng)網(wǎng)絡(luò)的輸入樣本，S參數(shù)作為輸出樣本,，進(jìn)行RBF網(wǎng)絡(luò)訓(xùn)練,。總共選取了100組樣點(diǎn)作為訓(xùn)練數(shù)據(jù),，另外又選取了100組不同的樣點(diǎn)作為神經(jīng)網(wǎng)絡(luò)模型性能的測試數(shù)據(jù),。頻率8.6GHz≤freq≤10.092 5GHz,。模擬S參數(shù)與輸入樣本間的關(guān)系：Y=F(X)，其中：X是神經(jīng)網(wǎng)絡(luò)的輸入變量,；Y是輸出變量,，Y=(|S₁₁|,|S₂₁|)。利用MATLAB軟件仿真輸出變量中|S₂₁|的仿真和訓(xùn)練結(jié)果如圖4～圖7所示,。其中,，圖4為RBF網(wǎng)絡(luò)的仿真曲線, 由此可見誤差非常小。圖5給出了達(dá)到預(yù)期的設(shè)計精度0.000 1所需的訓(xùn)練步數(shù)為35步,，此網(wǎng)絡(luò)很快即達(dá)到了設(shè)計精度,。為了驗證訓(xùn)練后的RBF網(wǎng)絡(luò)的性能，另選取100組樣點(diǎn)進(jìn)行測試,，其測試曲線如圖6所示,，RBF網(wǎng)絡(luò)的測試性能可由圖7所示，測試絕對誤差的絕對值小于0.03,，98%的測試相對誤差小于5%,，在|S21|衰減最大的拐點(diǎn)位置相對誤差較大，這是因為測試樣點(diǎn)在拐點(diǎn)處的選取沒能滿足實(shí)驗設(shè)計（DOE）原則,。仿真輸出再次說明RBF神經(jīng)網(wǎng)絡(luò)建模的性能相當(dāng)穩(wěn)定,。而且利用該神經(jīng)網(wǎng)絡(luò)進(jìn)行仿真設(shè)計的結(jié)果具有很好的可重復(fù)性，設(shè)計達(dá)到的效果令人滿意,。

?

??? 本文采用RBF神經(jīng)網(wǎng)絡(luò)對微波均衡器進(jìn)行了建模,。仿真設(shè)計的結(jié)果與網(wǎng)絡(luò)分析儀的測試結(jié)果進(jìn)行了比較，誤差較小,。這表明本文提出的神經(jīng)網(wǎng)絡(luò)模型設(shè)計方法使得微波均衡器的設(shè)計過程變得速度快,、精度高，具有準(zhǔn)確,、省時,、輔助設(shè)計等優(yōu)點(diǎn)。對于微波器件的分析設(shè)計具有很好的應(yīng)用價值,。