引言
浮點(diǎn)運(yùn)算" title="浮點(diǎn)運(yùn)算">浮點(diǎn)運(yùn)算作為數(shù)字信號處理中最常見的運(yùn)算之一,各大EDA軟件都帶有免費(fèi)的浮點(diǎn)運(yùn)算IP核。通過對IP核的生成和例化來實(shí)現(xiàn)浮點(diǎn)運(yùn)算,把FPGA" title="FPGA">FPGA設(shè)計(jì)者從繁重的代碼編寫中解脫了出來,同時可以對IP核進(jìn)行功能剪裁以避免對FPGA邏輯資源的浪費(fèi),實(shí)現(xiàn)最優(yōu)設(shè)計(jì)。但對浮點(diǎn)數(shù)的獲取卻關(guān)注很少。在浮點(diǎn)運(yùn)算中,單精度" title="單精度">單精度浮點(diǎn)以其極強(qiáng)的通用性得到了最廣泛的應(yīng)用。本文將目光集中在單精度浮點(diǎn)數(shù)的獲取上,為浮點(diǎn)IP核提供數(shù)據(jù)源。在數(shù)據(jù)的傳輸上,ASCII碼是經(jīng)常采用的一種形式,本文以串口接收到的ASCII碼所表示的實(shí)數(shù)為例,采用流水處理方式高速地將實(shí)數(shù)轉(zhuǎn)換為單精度浮點(diǎn)數(shù)。
1 實(shí)數(shù)轉(zhuǎn)換為單精度浮點(diǎn)數(shù)的原理
1.1 單精度浮點(diǎn)數(shù)格式
浮點(diǎn)數(shù)的表示遵循IEEE 754標(biāo)準(zhǔn),它由3部分組成:符號位(sign)、階碼(exponent)和尾數(shù)(fraction)。IEEE 754標(biāo)準(zhǔn)規(guī)定的單精度浮點(diǎn)數(shù)格式占用32位,包含:1位符號位s、8位帶偏移量的指數(shù)e[30:23]和23位尾數(shù)f[22:0],如圖1。單精度的指數(shù)使用正偏值形式表示,指數(shù)值的大小從1~254(0和255是特殊值)。采用該種形式表示是為了有利于比較大小,浮點(diǎn)小數(shù)在計(jì)算時,指數(shù)值減去偏正值即是實(shí)際的指數(shù)大小。其中偏移值(bias)為127,尾數(shù)有1位隱藏位。

單精度浮點(diǎn)數(shù)包含以下幾種情況:
(1)規(guī)格化數(shù):0
(2)(+0,-0):如果e=0且f=0,則V=(-1)s×0;
(3)非規(guī)格化數(shù):e=0但f≠0則V為非規(guī)格化數(shù);
(4)(+∞,-∞):e=255,且f=0,則V=(-1)s×∞;
(5)NaN(不是一個數(shù)):e=255,且f≠0,則V=NaN。
1.2 轉(zhuǎn)換原理
例如有一個實(shí)數(shù)為6.91,首先將其轉(zhuǎn)換為二進(jìn)制形式表示:110.1110100011110101110000101000。再將其規(guī)范化為如下:
6.91=1.101110100011110101110000101000×22則可以得到基本原型:
s:0;
e:2+127(十進(jìn)制)=129(十進(jìn)制)=10000001(二進(jìn)制);
f:101110100011110101110000101000(注:小數(shù)部分取28位,且小數(shù)點(diǎn)前面的1不要)。
小數(shù)部分取28位的目的在于更為準(zhǔn)確地表示實(shí)數(shù),后五位用于舍入處理。在IEEE 754標(biāo)準(zhǔn)中,舍入處理提供了4種可選方法:就近舍入、朝0舍入、朝+∞舍入和朝-∞舍入,本文采用就近舍入原則。就近舍入的實(shí)質(zhì)就是通常所說的“四舍五入”。例如:尾數(shù)超過規(guī)定的23位的多余數(shù)字是10010,多余位的值超過規(guī)定的最低有效值的一半。故最低有效位應(yīng)增1,若多余的5位是01111則簡單地截尾即可,對多余的5位100 00這種特殊情況:若最低有效位現(xiàn)為0,則截尾;若最低有效位現(xiàn)1,則向上進(jìn)一位使其變?yōu)?。所以,此例中要將最后5位作舍棄處理。得到的結(jié)果為:0 100000011011101000111101011100001。組合后等于0100 0000 1101 1101 0001 1110 1011 1000等于40DDIEB8。至此在原理上完成一個實(shí)數(shù)到單精度浮點(diǎn)數(shù)的轉(zhuǎn)換。
2 在FPGA中實(shí)現(xiàn)實(shí)數(shù)到單精度浮點(diǎn)數(shù)轉(zhuǎn)換的流程
2.1 轉(zhuǎn)換流程
在實(shí)際工程應(yīng)用中,所處理的數(shù)據(jù)都有一個或大或小的范圍,在這個范圍內(nèi)將實(shí)數(shù)轉(zhuǎn)換為單精度浮點(diǎn)數(shù)會節(jié)約芯片資源和降低功耗。故選擇在-9 999.999 9~9 999.999 9的范圍內(nèi)完成實(shí)數(shù)到單精度浮點(diǎn)數(shù)的轉(zhuǎn)換,如圖2所示。考慮到實(shí)際,數(shù)值在很多情況下是通過串口獲取的,并表現(xiàn)為ASCII形式。故本文中所提到的實(shí)數(shù)皆為ASCII表示。

轉(zhuǎn)換過程采用流水線操作,用計(jì)數(shù)器控制轉(zhuǎn)換進(jìn)程。ASCII碼轉(zhuǎn)換為單精度浮點(diǎn)的方法如下:
(1)將8位ASCII碼所代表的數(shù)字字符轉(zhuǎn)為十進(jìn)制數(shù)字(由于硬件電路對數(shù)字的表示只有0和1的組合,所以將實(shí)數(shù)的整數(shù)和小數(shù)分開表示);
(2)利用程序包里的數(shù)據(jù)類型轉(zhuǎn)換函數(shù)將十進(jìn)制數(shù)轉(zhuǎn)換為二進(jìn)制數(shù),但小數(shù)部分的轉(zhuǎn)換需要單獨(dú)實(shí)現(xiàn);
(3)對二進(jìn)制表示的實(shí)數(shù)進(jìn)行規(guī)格化;
(4)根據(jù)符號位ASCII碼值確定符號位s,根據(jù)規(guī)格化移動的位數(shù)確定階碼e,將規(guī)格化中的小數(shù)部分f保留28位;
(5)根據(jù)就近舍入原則對保留的28位小數(shù)部分的后5位進(jìn)行判斷和舍入。2.2 關(guān)鍵代碼解析
在FPGA的硬件描述語言中將整數(shù)的十進(jìn)制轉(zhuǎn)換為二進(jìn)制比較簡單,可以調(diào)用ISE軟件自帶的程序包中的轉(zhuǎn)換函數(shù)來實(shí)現(xiàn),但如何將小數(shù)部分轉(zhuǎn)換為二進(jìn)制是能否順利完成從實(shí)數(shù)到單精度浮點(diǎn)數(shù)轉(zhuǎn)換的關(guān)鍵。考慮到要對小數(shù)部分進(jìn)行舍入運(yùn)算,所以將小數(shù)部分轉(zhuǎn)換28位的二進(jìn)制。要用28位二進(jìn)制表示小數(shù)部分,需利用VHDL語言中變量(variable)被賦值時立即生效的特性,結(jié)合FOR循環(huán)來實(shí)現(xiàn)。部分關(guān)鍵代碼如下:

代碼中frac_part是小數(shù)部分的十進(jìn)制表示(因?yàn)閕nteger類型只能表示整數(shù),所以將小數(shù)部分?jǐn)U大了10 000倍,但不影響結(jié)果的正確性),frac_28是小數(shù)部分的二進(jìn)制表示。信號frac_28(27)的權(quán)值是2-1,依次以1/2倍率遞減,frac_28(0)的權(quán)值是2-28。此進(jìn)程由frac_part發(fā)生變化來啟動,完成轉(zhuǎn)換的時間是瞬時,也可以認(rèn)為是一個時鐘周期。
3 仿真結(jié)果及分析
首先用ModelSim進(jìn)行功能仿真,其結(jié)果如圖3所示。輸入的實(shí)數(shù)為125.763,輸出結(jié)果經(jīng)Matlab逆向求值同輸入值進(jìn)行比較,驗(yàn)證了轉(zhuǎn)換結(jié)果的正確性。一個數(shù)的正確轉(zhuǎn)換并不能說明問題,下面將驗(yàn)證此轉(zhuǎn)換方法的可行性。

選取具有代表性的實(shí)數(shù)對轉(zhuǎn)換方法的性能進(jìn)行驗(yàn)證。主要驗(yàn)證兩個方面:
(1)是否在預(yù)定域內(nèi)具有全覆蓋性;
(2)是否能對此域中的最小值進(jìn)行有效表示。
結(jié)果如表1所示。
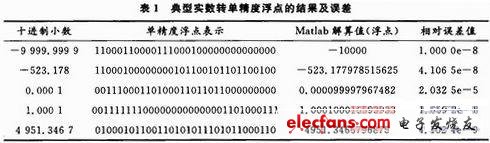
根據(jù)轉(zhuǎn)換原理,最小值所轉(zhuǎn)換的誤差最大,但最大值的轉(zhuǎn)換誤差不一定最小(因?yàn)榇嬖谏崛?。這個最大的轉(zhuǎn)換誤差在10-5量級,當(dāng)待轉(zhuǎn)換實(shí)數(shù)的絕對值大于整數(shù)1時,轉(zhuǎn)換的誤差將小于10-5量級,可達(dá)10-9量級。這樣的轉(zhuǎn)換誤差可以滿足大多數(shù)浮點(diǎn)運(yùn)算環(huán)境下的精度需要。實(shí)驗(yàn)驗(yàn)證了此轉(zhuǎn)換方法的有效性和“全覆蓋性”。
在完成仿真測試后,將程序進(jìn)行綜合,布局布線,最后生成位流文件下載到FPGA芯片中進(jìn)行驗(yàn)證。在實(shí)際的芯片中將轉(zhuǎn)換結(jié)果和已仿真得到的結(jié)果進(jìn)行比較,并輸出指示信號。從實(shí)際的電路輸出結(jié)果看,和仿真結(jié)果完全一致,證明了此方法在實(shí)際芯片中可行性。因?yàn)椴捎玫氖橇魉€操作,所以仿真所用的周期數(shù)和實(shí)際周期數(shù)是一致的。該實(shí)驗(yàn)在50 MHz的時鐘下用時6個周期(即0.12μs)完成轉(zhuǎn)換操作。而在最常用的串口傳輸波特率9 600 b/s下,傳送1個碼元的時間為10-1ms量級。從而可以得出:完成從ASCII碼所表示的實(shí)數(shù)(-9 999.999 9~+9 999.999 9)到單精度浮點(diǎn)的轉(zhuǎn)換所用的時間將在10-1μs量級以下,具有較高的實(shí)時性。
4 結(jié)語
本文的實(shí)現(xiàn)向單精度浮點(diǎn)的轉(zhuǎn)換占用1 161個slice資源,在FPGA發(fā)展到今天,F(xiàn)PGA的容量和資源都有了很大提高的情況下,這樣的資源占用量在大多數(shù)應(yīng)用中是可以承受的。本文的設(shè)計(jì)可以很容易地根據(jù)實(shí)際實(shí)數(shù)的范圍進(jìn)行調(diào)整,并且可以推廣到其他浮點(diǎn)格式,可有效地為浮點(diǎn)IP核提供快速且具有高精度的數(shù)據(jù)源。

