摘 要： 旋轉,、縮放和平移(RST)等幾何攻擊能夠破壞水印檢測的同步性,，使得水印檢測失敗。針對此問題,，提出了一種基于圖像局部Zernike矩的RST不變零水印算法,。Zernike矩的幅度具有旋轉不變性，再結合圖像歸一化,，使其具有縮放和平移不變性,。由于Zernike矩的圖像重構效果不理想且重構過程中復雜度高，因此水印嵌入選擇零水印方案,。實驗結果表明,，該算法對旋轉、縮放和平移(RST)的攻擊具有很好的魯棒性,，同時對JPEG壓縮,、加噪,、濾波等常見的圖像處理操作也具有很好的魯棒性。
關鍵詞： 零水??； 旋轉、縮放和平移(RST),； Zernike矩,； 圖像歸一化
隨著多媒體數(shù)字產(chǎn)品的快速發(fā)展，人們可以隨意訪問每個數(shù)字圖像,，并能對圖像對象進行旋轉,、縮放、平移等各種幾何操作,。幾何攻擊能極大地破壞水印檢測的同步性,，即使微小的幾何攻擊也可能使水印檢測失敗,這使得數(shù)字圖像水印技術變得更加復雜，因此,，開發(fā)一種能有效抵抗旋轉,、縮放和平移 (RST)等幾何攻擊的圖像水印技術迫在眉睫。
在抗幾何攻擊的水印方法中,，不少算法利用了圖像的各種不變矩,目前常用的矩主要有幾何矩,、中心矩和正交不變矩。Zernike矩的基是正交徑向多項式,，可以保證所提取的特征相關性小,、冗余性小,；與其他不變矩相比,， Zernike矩還具有旋轉不變性、對噪聲的魯棒性以及多層次表達等優(yōu)點,，為此,，開始探索將Zernike 矩引入抗幾何攻擊的圖像水印算法中。
針對上述問題,，本文提出計算圖像局部重要區(qū)域Zernike矩的抗幾何攻擊的水印算法,。由于圖像在受到旋轉、縮放和平移 (RST)等幾何攻擊時,，圖像的中心不會發(fā)生變化,，因此選取以圖像的中心為原點，并采用圖像邊緣檢測的方法,，找到包含圖像對象的局部重要區(qū)域,，從而減小由于旋轉帶來的邊緣影響，提高了Zernike矩的旋轉不變性。然后,，結合圖像的縮放歸一化,，實現(xiàn)水印對縮放攻擊的魯棒性。由于Zernike矩的圖像重構效果并不理想,，而且重構過程中需要高階矩,，計算復雜度較高。因此,，在水印算法的設計中，不能通過直接修改原始圖像的Zernike矩并進行重構來嵌入水印,，所以水印嵌入選用零水印方案,。實驗結果表明，該算法對旋轉,、縮放和平移(RST)的攻擊具有很好的魯棒性,，同時對JPEG壓縮、加噪,、濾波等常見的圖像處理操作也具有魯棒性,。
1 Zernike 矩及其性質
1.1 Zernike矩的定義
Zernike于1934年提出了一組多項式{Vnm(x,y)}，這組多項式在單位圓(x2+y2≤1)內是完備正交的,，其形式[1]為：
3 實驗及結果
實驗選取256×256的lena,、128×128的camera和128×128的akiyo作為原始測試圖像，為簡單起見,，只考慮原始圖像中僅含一個圖像對象且圖像背景較為單一的情況,。
證明該算法的可行性，256×256的lena,、128×128的camera和128×128的akiyo三幅圖像完全不相關,其中l(wèi)ena圖像與camera圖像的水印序列相似率sim=0.574 257<0.7,，lena圖像與akiyo圖像的水印序列相似率sim=0.514 851<0.7，camera圖像與akiyo圖像的水印序列相似率sim=0.603 960<0.7,。大量實驗證明,，不同圖像由零水印構造的二值水印序列相似率都不會大于0.7。
為了測試該算法的魯棒性,，用各種幾何操作對圖像進行攻擊實驗,。
3.1 旋轉攻擊
在數(shù)字圖像處理領域中， 圖像旋轉有兩種不同的形式[8]：Crop rotation和Loose rotation,。Akiyo圖像在兩種不同形式下旋轉30°后的水印圖像如圖 1(b)和圖1(e)所示,。
Crop rotate攻擊后，本文算法水印檢測響應曲線如圖 1(a)所示,，其中橫軸表示旋轉角度,。可以看出,，本文算法對于Crop rotate攻擊,，檢測的相似度都在0.95以上,。
Loose rotate攻擊后，本文算法和參考文獻[10]中的算法水印檢測響應曲線分別如圖 1(c)和圖1(d)所示,，其中橫軸表示旋轉角度,。可以看出,，本文算法對于Loose rotate攻擊,，檢測的相似度都在0.92以上，相比于參考文獻[10]中的算法,，魯棒性有一定的提高,。
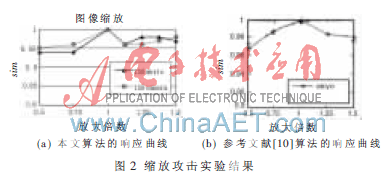
3.2 縮放攻擊
縮放攻擊后，本文算法和參考文獻[10]算法水印檢測的響應曲線分別如圖 2(a)和圖2(b)所示,，其中橫軸表示放大倍數(shù),。對于縮放攻擊，本文算法和參考文獻[10]算法的魯棒性能基本一致,。
3.3 噪聲攻擊
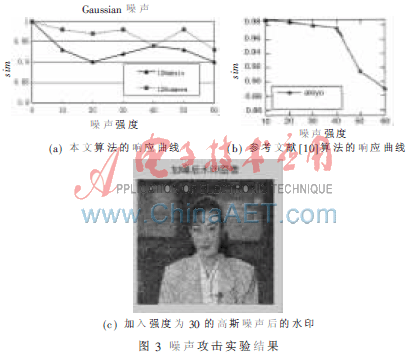
加入不同高斯噪聲后,本文算法和參考文獻[10]的算法水印檢測響應曲線分別如圖 3(a)和圖3(b)所示,，其中橫軸表示噪聲強度。Akiyo加入強度為30的高斯噪聲后的水印圖像如圖3(c)所示,。對于噪聲攻擊,，本文算法和參考文獻[10]的算法,相比魯棒性能有一點下降。
3.4 濾波攻擊
濾波攻擊后,，本文算法和參考文獻[10]的算法水印檢測響應曲線如圖4(a)和圖4(b)所示,，其中橫軸從左到右依次表示為沒有受到攻擊、5×5中值濾波,、3×3中值濾波,、3×3均值濾波、5×5均值濾波,。Akiyo經(jīng)過5×5均值濾波后的水印圖像如圖 4(c)所示,。對于濾波攻擊，本文算法和參考文獻[10]算法的魯棒性能幾乎一樣,。
3.5 壓縮攻擊
圖像經(jīng)JPEG壓縮攻擊后,，本文算法和參考文獻[10]算法的水印檢測響應曲線如圖 5(a)和圖5(b)所示，其中橫軸表示壓縮質量百分數(shù),。Akiyo受到壓縮質量百分數(shù)為20%的JPEG壓縮后的水印圖像如圖 5(c)所示,。對于低質量壓縮攻擊，相比于參考文獻[10]的算法,本文算法的魯棒性有一定提高,。
利用歸一化后的Zernike 矩的幅度具有RST不變的性質,，將從圖像中提取的局部Zernike矩的幅度矢量作為圖像的特征矢量，二值化后作為零水印，實現(xiàn)了具有RST不變性的水印,。實驗結果表明,，該算法對旋轉、縮放和平移(RST)的攻擊具有很好的魯棒性,，同時對JPEG壓縮,、加噪、濾波等常見的圖像處理操作也具有很好的魯棒性,。
參考文獻
[1] KHOTANZAD A, HONG Y H. Invariant image recognition by Zernike moments[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990,12(5):489-497.
[2] KINTNER E C. On the mathematical properties of Zernike polynomials[J].Optica Acta, 1976,23(8):679-680.
[3] 葉斌,彭嘉雄. Zernike 矩不變性分析及其改進[J].紅外與激光工程, 2003(01):37-41.
[4] 馬建湖,何甲興.基于小波變換的零水印算法[J].中國圖象圖形學報, 2007,12(4):581-585.
[5] KHOTANZAD A, HONG Y H. Invariant image recognition by Zernike moments[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990,12(5):489-497.
[6] XIN Y Q,LIAO S,PAWLAK M,et al. Geometrically robust image watermark via pseudo-Zernike moments[A].CCECE, 2004:0939-0942.
[7] 李雷達,郭寶龍,孫磊. 基于局部Zernike矩的RST不變水印[J]. 光電子·激光, 2007,18(1):117-120.
[8] Image processing toolbox: imroate function. http://www.mathworks.com/access/helpdesk_r13/help/toolbox/images/imrotate.html.
[9] Xiang Shijun. On invariance analysis of Zernike moments in the presence of rotation with crop and loose modes[J].Multimed Tools Appl,2010,25(5).
[10] 徐達文,王繼成,王讓定. 基于Zernike 矩的視頻對象零水印算法[J].中國圖象圖形學報, 2009,，14(9):1825-1831.