動彈性模量(Dynamic Young's Modulus)是建筑工程設(shè)計中混凝土等剛性材料的力學(xué)性能的一個重要參數(shù),反映了某段時間內(nèi)材料在外力作用下的細(xì)微形變,因此動彈性模量的測量在建筑工程的質(zhì)量監(jiān)控與評估中有著重要的意義?；炷恋膹椥阅Ａ渴穷l率的單值函數(shù),該函數(shù)的關(guān)鍵變量是混凝土試件的共振頻率,即由試件的諧振頻率,可推算出其強(qiáng)度來,。由此,混凝土的強(qiáng)度測量可以簡化為先進(jìn)行動彈諧振頻率測量,再計算動彈性模量的過程[1]。
    當(dāng)前剛性材料的動彈性模量測量方法有掃頻法,、快速傅里葉變換法(FFT)等,。在掃頻法中,先由激振器從低頻到高頻依次發(fā)射振動波到待測試件表面,迫使其產(chǎn)生非平穩(wěn),、瞬態(tài)的反饋振動波形,通過不同頻率間反饋波形幅值的比較,掃描出諧振頻率點(diǎn),。而FFT法是在數(shù)字電路快速發(fā)展的背景下,由數(shù)字處理器對反饋波形進(jìn)行快速離散傅里葉變換,計算出功率譜中的峰值頻率作為諧振頻率。在FFT算法中,消除了掃頻法中激振器在不同頻率下激振波振幅的誤差影響,。而FFT算法在有限的采樣點(diǎn)下,其低頻精度較低(頻譜范圍為20 kHz時,誤差在±20 Hz以上),。為此,本文將小波變換中的多分辨分析方法引入到動彈性模量的測量中來,可在現(xiàn)有傳感器硬件電路基礎(chǔ)上,通過在DSP平臺上的Mallat算法實(shí)現(xiàn)高精度的頻譜計算,提高諧振頻率測量精度,消除因傳感器不一致所導(dǎo)致的誤差影響,從而提高動彈性模量測量的準(zhǔn)確度。
1 Mallat算法的頻譜分析原理
1.1 Mallat算法原理及分解過程
    Mallat算法是小波信號處理中最常用的小波快速算法,。連續(xù)小波變換是指：把某一被稱為基本小波(亦稱母小波或基波)的函數(shù)Ψ(t)作位移τ后,在不同尺度α下再與待分析信號x(t)作內(nèi)積[2],。
    
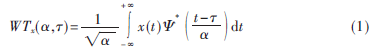
    Mallat算法主要是用基于多分辨分析的多采樣濾波器組來分解信號,可以把信號分解為離散平滑分量和離散細(xì)節(jié)分量。這些離散分量間的關(guān)系可用濾波器組的形式表現(xiàn),。Mallat算法的小波分解公式：


上式中,，Edt為橫向動彈性模量,單位為Pa；G是試件質(zhì)量,單位為kg,；fmax是在外力作用下試件諧振時的峰值頻率,；l、b,、h分別對應(yīng)試件的長,、寬和高,單位為mm；R是取決于試件邊長及泊松比的修正系數(shù),對于l/h=4,、泊松比大約為1/6的混凝土試件,R取1.5,。在混凝土等硬質(zhì)材料的動彈性模量的測量中,當(dāng)溫度與濕度等外界環(huán)境因素穩(wěn)定時，式(8)中其他變量的測量誤差較小,，難點(diǎn)是非平穩(wěn)狀態(tài)的測試波形的頻譜計算,。每個試件因?yàn)榻Y(jié)構(gòu)的差異及縫隙的存在,其共振頻率都有若干個,稱其為共振頻率帶,在力學(xué)測量中,建筑力學(xué)設(shè)計中的動彈性模量測試只研究其低頻段(≤20 kHz)內(nèi)的共振頻率。
    測量過程硬件框圖如圖2所示,激振器由密封在鋼制圓柱體內(nèi)腔的大功率動圈揚(yáng)聲器構(gòu)成,垂直安裝在揚(yáng)聲器錐盆上的鋁制測桿伸出腔外3 mm,。拾振器構(gòu)造與激振器類似,但揚(yáng)聲器由靈敏度較高的壓電陶瓷片替換,。在測量前,首先將激振器正對混凝土試件側(cè)面的中心位置,拾振器則放置在試件同一面的側(cè)邊沿,保持激振器和拾振器的測桿都輕輕地接觸在混凝土試件表面上(測桿與試件的接觸面涂抹一薄層耦合介質(zhì)),。

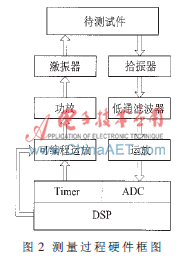
　測量過程中,首先由DSP調(diào)制出PWM信號,通過可編程運(yùn)放(PGA)調(diào)整波形幅度后,再經(jīng)功放電路功率放大后連接到激振器的正負(fù)極。激振器的測桿將激勵信號施加到混凝土試件中間點(diǎn), 試件在外力作用下振動,。由于壓電效應(yīng),拾振器中的壓電陶瓷片將試件因受迫振動而產(chǎn)生的機(jī)械波轉(zhuǎn)換為電壓信號(Vp-p<1 mV),該非平穩(wěn)電壓信號經(jīng)低通濾波器濾除高頻干擾后送至由LM833構(gòu)成的單端運(yùn)放電路放大1 000倍,其濾波放大電路如圖3所示,。

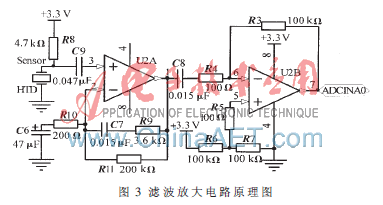
    放大的電壓信號接入DSP的ADCINA0管腳,DSP以固定的采樣頻率對該電壓信號進(jìn)行模數(shù)轉(zhuǎn)換,所得的數(shù)組x(n)作為Mallat算法的原始處理數(shù)據(jù)源(每次算法的采樣點(diǎn)數(shù)N=1 024)。當(dāng)激勵源的激勵頻率接近于試件的固有頻率時,產(chǎn)生共振效應(yīng),試件強(qiáng)迫振動的振幅及功率達(dá)到最大,通過算法計算出的峰值頻率fmax作為試件的共振頻率,。
3 Mallat算法測量諧振頻率過程分析
3.1 DSP中Mallat算法的程序設(shè)計方法
    在動彈性模量測量中, Mallat算法是基于TMS320F2808型32位定點(diǎn)數(shù)字信號處理器(DSP)平臺實(shí)現(xiàn)的,。基于哈佛總線結(jié)構(gòu)的F2808型DSP最高運(yùn)算速度為100 MIPS,其內(nèi)置的12位ADC模塊最小轉(zhuǎn)換時間為160 ns,。針對剛性材料的共振頻率低頻段分布的特點(diǎn),由Nyquist抽樣定理可知模數(shù)轉(zhuǎn)換單元的最小采樣頻率為40 kHz,但為了減小能量泄漏及幅值失真,采樣頻率fs設(shè)定為采樣點(diǎn)數(shù)N的整數(shù)倍,即fs=40.96 kHz,。
    程序中設(shè)置16位的ePWM模塊作為激振器的信號源：首先將來自系統(tǒng)的時鐘信號通過PLL (鎖相環(huán))預(yù)分頻到10 kHz,修改周期寄存器TyPR以改變輸出PWM方波的頻率。
    在DSP程序設(shè)計中,為了提高系統(tǒng)運(yùn)算效率,Mallat算法操作通過C語言嵌套匯編語言實(shí)現(xiàn):在C函數(shù)的框架中,匯編語句通過動態(tài)參數(shù)傳遞的形式進(jìn)行調(diào)用,并且對相應(yīng)C語句進(jìn)行優(yōu)化,以減少函數(shù)的調(diào)用次數(shù),。DSP中,當(dāng)RPT流水線啟動后,通過循環(huán)尋址指令間接地在RAM空間構(gòu)造的循環(huán)緩存區(qū)中調(diào)用采樣序列x(n),DSP可在單指令周期內(nèi)通過硬件乘法器實(shí)現(xiàn)快速乘加操作,以便迅速完成卷積,、濾波等小波運(yùn)算。

4 試驗(yàn)分析及結(jié)果
　　為驗(yàn)證測試系統(tǒng)中算法的精確度,在試驗(yàn)電路中：DSP的PWM周期定時器設(shè)定值FT從50 Hz~1 kHz范圍內(nèi)以0.25 Hz/ms增加,當(dāng)FT達(dá)到1 kHz后,，以1 Hz/ms增加到5 kHz為止,；為了減小激振器中電磁線圈的溫漂,將PWM的脈寬調(diào)制為0.3,激振器輸出平均功率PT=5 W；功率譜計算時間平均為3.2 ms,；圖5是標(biāo)準(zhǔn)試件頻譜圖的打印輸出結(jié)果,。
    由圖5可知,峰值頻率fmax=1.502 kHz,即該試件的諧振頻率為1.502 kHz,符合一般情況下混凝土的諧振頻率分布。對于l=400 mm,、b=h=100 mm的標(biāo)準(zhǔn)試件,當(dāng)其質(zhì)量G=10.0 kg時,由式(8)計算出動彈性模量Edt為20.90 GPa,。

　由于通常制備的混凝土試件的共振頻率分布不均勻且難以預(yù)測[7]。試驗(yàn)中,為了測試系統(tǒng)的計量準(zhǔn)確度,使用了函數(shù)信號發(fā)生器來模擬激振波形：信號源輸出不同中心頻率下峰值為0.5 mV的sinx/x周期函數(shù)波形,利用DSP硬件平臺測試FFT算法與Mallat算法在同樣采樣點(diǎn)數(shù)下的諧振頻率測量的相對誤差,結(jié)果如表1所示,。
    由表1可知,測試平臺在20 kHz量程時,FFT算法的低頻段相對誤差較大,在高頻段與Mallat算法相同,而Mallat算法測量頻譜的相對誤差始終小于0.3%,。所以,兩種算法相對于量程的精度相同,而由于Mallat算法的多尺度分析等特點(diǎn),其在低頻段內(nèi)諧振頻率測量值的可信度更高,相對于常規(guī)FFT算法有效提高了動彈性模量的測量精度。

　本文通過在DSP平臺上實(shí)現(xiàn)Mallat算法,運(yùn)用離散小波變換的多分辨率分析方法對非平穩(wěn)的諧振波形進(jìn)行頻譜分析,。利用其多尺度測量由粗至細(xì)提取出激振信號的局部頻域特征,再通過小波改進(jìn)算法去除頻率混淆,可快速準(zhǔn)確地掃描出其中的功率峰值點(diǎn)以作混凝土等剛性材料的動彈性模量計算,。
　通過Mallat算法的多分辨率分析方法,保證了測試系統(tǒng)在20 kHz量程內(nèi)相對誤差小于0.3%,重復(fù)性誤差小于0.5%,滿足了建筑工程設(shè)計中混凝土動彈性模量測量的精度需求。在利用Mallat算法研究聲信號頻譜的基礎(chǔ)上,可通過超聲波定位精度高,、穿透能力強(qiáng)等特點(diǎn)來進(jìn)行混凝土結(jié)構(gòu)件的探傷定位等無損檢測研究,。
參考文獻(xiàn)
[1] 劉飛,王海飚,翁麗婭，等.基于小波理論對混凝土損傷特性的試驗(yàn)研究[J].巖土力學(xué)與工程學(xué)報,2005,24(14):2581-2587.
[2] 楊福生.小波變換的工程分析與應(yīng)用[M]. 北京:科學(xué)出版社,2001：58-72.
[3] MALLAT S.信號處理的小波導(dǎo)引[M].北京:機(jī)械工業(yè)出版社,2002：388-397.
[4] 侯正信,王成優(yōu),楊愛萍.有限長度信號Mallat算法的邊界延拓方法[J].數(shù)據(jù)采集與處理,，2009,24(6):714-720.
[5] PATIL S, ABEL E W. Real time continuous wavelet transform implementation on a DSP processor[J]. Journal of  Medical Engineering & Technology, 2009, 33(3):223-231.
[6] 封常生.小波分析在信號處理中的應(yīng)用[D].上海:上海交通大學(xué),2007.34-50.
[7] SUZUKI T, OHTSU M et al. Relative damage evaluation of concrete in a road bridge by AE rate-process analysis [J]. Materials and Structures, 2006,40(2):221-227.