文獻(xiàn)標(biāo)識碼: A
文章編號: 0258-7998(2012)03-0041-03
在TD-LTE系統(tǒng)中,Zadoff-Chu(ZC)序列主要應(yīng)用于上行RS序列生成、PRACH前導(dǎo)序列生成以及主同步信號生成等[3],它在整個TD-LTE系統(tǒng)中扮演著重要的角色,是建立上下行鏈路同步以及信道估計(jì)中不可或缺的一部分。Zadoff-Chu序列具有良好的自相關(guān)性和互相關(guān)性,這有利于減少不同前導(dǎo)之間的相互干擾,而且其本身具有對稱性,這有利于減少序列生成的復(fù)雜度。同時LTE系統(tǒng)選擇了素數(shù)長度的Zadoff-Chu序列,保證序列檢測性能的提高。
本文通過對ZC序列生成的分析以及自身的特性,結(jié)合理論推導(dǎo),提出了一種簡化的ZC生成算法的DSP實(shí)現(xiàn)方案,并通過仿真與比較,驗(yàn)證了該方案的可行性,能夠滿足LTE系統(tǒng)性能的要求。
1 Zadoff-Chu算法分析
參數(shù)為u,序列長度為Nzc的ZC序列定義為:

每計(jì)算一次Xu(n)的值,在求x的計(jì)算上就需要3次乘法和一次除法運(yùn)算。對于長度為Nzc的序列而言,計(jì)算所有Xu(n)的指數(shù)x需要3×Nzc次的乘法和Nzc次的除法運(yùn)算,然后利用式(2)計(jì)算每一個Xu(n)的值。
用式(2)計(jì)算Zadoff-Chu序列的生成存在兩點(diǎn)不足:(1)余弦和正弦運(yùn)算屬于一種非線性的運(yùn)算,多次運(yùn)算的復(fù)雜度很高,耗時很長,不利于滿足LTE系統(tǒng)實(shí)時性的要求;(2)MS320C6000系列DSP在軟件的實(shí)現(xiàn)中只能處理定點(diǎn)數(shù)運(yùn)算,無法直接對浮點(diǎn)數(shù)進(jìn)行處理。因而要利用式(2)計(jì)算必須對正弦和余弦進(jìn)行量化處理。
在定點(diǎn)DSP芯片中,采用定點(diǎn)數(shù)進(jìn)行數(shù)值運(yùn)算,其操作數(shù)一般采用整型數(shù)表示。一個整型數(shù)的最大表示范圍取決于DSP芯片所給定的字長,一般為16 bit或32 bit。對DSP芯片而言,參與數(shù)值運(yùn)算的數(shù)就是16 bit的整型數(shù)。通過設(shè)定小數(shù)點(diǎn)在16 bit數(shù)中的不同位置,就可以表示不同大小和不同精度的小數(shù)。數(shù)的定標(biāo)有Q表示法和S表示法兩種,如表1所示。
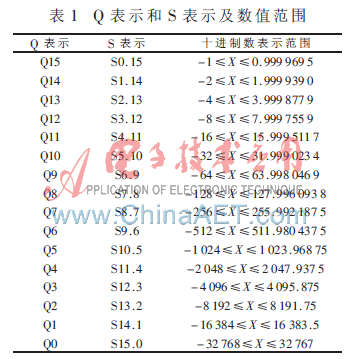
從表1可以看出,不同的Q所表示的數(shù)不僅范圍不同,而且精度也不相同。Q越大,數(shù)值范圍越小,但精度越高;相反,Q越小,數(shù)值范圍越大,但精度就越低。本文采用Q量化方法,浮點(diǎn)數(shù)與定點(diǎn)數(shù)的轉(zhuǎn)換關(guān)系可表示為:浮點(diǎn)數(shù)(x)轉(zhuǎn)換為定點(diǎn)數(shù)(xq):xq=(int)x×2q
式中int表示下取整。由正弦和余弦的范圍,結(jié)合表1可知,可以采用Q15進(jìn)行浮點(diǎn)數(shù)到定點(diǎn)數(shù)的轉(zhuǎn)化。為了減少正弦和余弦由于非線性造成的復(fù)雜運(yùn)算,可以采用查表的方法。首先對sin(x)的0~π的值進(jìn)行量化處理,根據(jù)sin(x)本身的對稱性可以通過0~π的量化值取反得到;其次,根據(jù)正弦和余弦之間的關(guān)系cos(x)=sin(x+π/2),可以將余弦值的求法轉(zhuǎn)化到求正弦上。由于量化存在著誤差,因而量化的點(diǎn)數(shù)越多,所求的值越接近理論上的值,但量化點(diǎn)數(shù)越大占用的內(nèi)存空間也越大。在0~?仔在之間進(jìn)行2 048點(diǎn)量化時,已十分接近理論值。因此采用0~π在之間進(jìn)行2 048點(diǎn)量化。
進(jìn)一步對式(1)推導(dǎo)發(fā)現(xiàn):

由式(4)可知,對于給定的參數(shù)u,A(n)/A(n-1)為定值,對于初始值A(chǔ)(0)=1,XU(0)=1。通過式(3)和式(4)的遞推關(guān)系就可以只通過乘法運(yùn)算計(jì)算出ZC序列,在計(jì)算時只需要計(jì)算一次正弦和余弦即可。用這種方法將正弦和余弦轉(zhuǎn)化成復(fù)數(shù)的乘法運(yùn)算,減少了正弦和余弦歸一化和量化查表的時間,進(jìn)一步降低運(yùn)算的復(fù)雜度。
由ZC序列本身所具有的性質(zhì)可知:

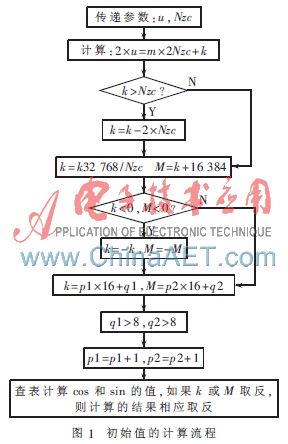
首先把遞推公式的初始值A(chǔ)(0)=1和Xu(0)=1分別用MVK指令賦值到相應(yīng)的寄存器中。由遞推關(guān)系式,首先計(jì)算出A(n),由于A(n-1)和計(jì)算出的旋轉(zhuǎn)因子M均為復(fù)數(shù),不能直接進(jìn)行相應(yīng)的乘法運(yùn)算,只能采用復(fù)數(shù)相乘的法則。即A(n)的實(shí)部等于A(n-1)和M的實(shí)部與虛部分別相乘后再進(jìn)行相減。為了減少指令的開銷,可以采用DOTPN2指令,該條指令可以直接完成A(n-1)的實(shí)部和虛部與M的實(shí)部和虛部相乘之后相減,把得到的實(shí)部用SHR指令進(jìn)行右移16 bit,保證得到的結(jié)果為半字。同樣A(n)的虛部的計(jì)算,先用匯編指令PACK2交換M的實(shí)部和虛部,再用DOTP2指令完成A(n-1)和M的高16 bit和低16 bit的相乘以及A(n-1)和M的低16 bit和高16 bit的相乘之后再相加,同樣用SHR指令對虛部的計(jì)算結(jié)果右移16 bit,保證虛部在半字的范圍內(nèi)。計(jì)算完成A(n)后,再把A(n)和Xu(n-1)進(jìn)行復(fù)數(shù)相乘,從而得到Xu(n)的計(jì)算結(jié)果。由ZC序列本身所具有的對稱性,分別將計(jì)算出的Xu(n)的實(shí)部和虛部用STH指令分別壓棧到輸出結(jié)果的第n個字和第Nzc-n-1個字中,至此ZC序列的計(jì)算全部完成。
3 性能分析與總結(jié)
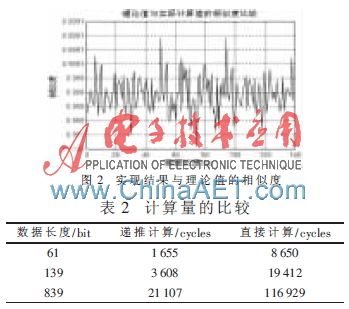
通過DSP軟件實(shí)現(xiàn)得到的結(jié)果與用MATLAB搭建的鏈路得到的理論數(shù)據(jù)進(jìn)行比較,如圖2所示。圖2雖然只是長度Nzc=139點(diǎn),但不失一般性。從圖中可以看出,雖然量化誤差的存在,但是在2 048點(diǎn)對sin在(0,π)區(qū)間進(jìn)行量化時,得到的結(jié)果與理論數(shù)據(jù)的值相差在0.1%左右。同時在應(yīng)用DSP軟件實(shí)現(xiàn)中,盡量對程序進(jìn)行優(yōu)化,通過指令并行,操作碼的合理設(shè)計(jì)以及減少或消除程序中的’NOP’指令[6]等方法進(jìn)行優(yōu)化。當(dāng)運(yùn)用TMS320C64×DSP芯片實(shí)現(xiàn)時,由于處理器的超高主頻一般為1 GHz,所以一個指令周期耗時為1 ns,其運(yùn)算速率非常快,如表2所示,與直接進(jìn)行ZC序列的生成相比較大大降低了運(yùn)算時間,可以滿足LTE系統(tǒng)的快速有效性。
本文從理論分析出發(fā),根據(jù)TD-LTE系統(tǒng)特性以及Zadoff-Chu序列本身的性質(zhì),提出了一種簡單有效的Zadoff-Chu算法實(shí)現(xiàn)方案,并將該算法在TMS320C64×芯片上實(shí)現(xiàn)。程序運(yùn)行結(jié)果表明,提出的算法具有可行性和高效性,能夠滿足TD-LTE系統(tǒng)的需求。該方案已在LTE-TDD無線綜合測試儀表的開發(fā)中得到了應(yīng)用。
參考文獻(xiàn)
[1] 丁玉美.數(shù)字信號處理[M].西安:西安電子科技大學(xué)出版社,2002.
[2] 何方白,張德民.數(shù)字信號處理[M].北京:高等教育出版社,2009.
[3] 3GPP TS 36.211 v9.0.0 Evolved universal terrest-rial radio access(E-UTRA) physical channels and modulation (release 9)[S].2009-12.
[4] SAIDI A.Decimation-in-time-frequency FFT algorithm, Manuscript,To be published.1993(8).
[5] Texas Instruments Incorporated.TMS320C64x/C6-4x+DSP. CPU.and.Instruction.Set.Reference.Guide[E-B/OL].Http://www.ti.com.cn,2008.
[6] Texas Instruments Incorporated.TMS320C6000系列DSP編程工具與指南[M].田黎育,何佩琨,朱夢宇,譯.北京:清華大學(xué)出版社,2006:32-50.
[7] 馮僑,鄧娟,沈靜,等.LTE系統(tǒng)中ZC序列的實(shí)現(xiàn)方法[P]:CN 101826890 A.2010.09.08.

