摘  要： 針對(duì)解碼圖像的方塊效應(yīng)，提出了一種基于分形編碼分辨率無(wú)關(guān)性的新的解決方案,。在低分辨率下解碼圖像后,，結(jié)合雙線(xiàn)性與最近鄰點(diǎn)插值方法還原圖像。在不改變?cè)幋a的前提下,，該算法有效地減少了解碼圖像的方塊效應(yīng),。
關(guān)鍵詞： 分形編碼；圖像壓縮,；分辨率無(wú)關(guān),；方塊效應(yīng)

    分形圖像壓縮技術(shù)以其高壓縮比的潛在性能在圖像壓縮領(lǐng)域倍受重視，被認(rèn)為是第二代圖像壓縮編碼技術(shù)的三大方法之一[1],。分形編碼的潛在壓縮比高,，運(yùn)算速度不受圖像灰度值分辨率高低的影響，而且編碼文件大小與灰度值無(wú)關(guān)[2],。但是,，其算法復(fù)雜度高，從而導(dǎo)致圖像的自相似性不強(qiáng),，特別在高壓縮比下,，會(huì)造成恢復(fù)圖像中相鄰圖像塊的邊界銜接不連續(xù)，就是所謂的塊狀效應(yīng),，使自然圖像無(wú)法達(dá)到高效壓縮,。
    目前，分形編碼所面臨的最主要問(wèn)題就是如何在提高編碼速度,、保證高壓縮比和提高解碼質(zhì)量三者之間找到平衡點(diǎn),。為此，分形的研究主要從兩方面進(jìn)行：(1)通過(guò)分形編碼自身算法的改進(jìn)，如改變圖像分割方式,、值域塊定域塊的分類(lèi),、減少搜索范圍等；(2)與其他算法混合編碼,，如通過(guò)與矢量量化結(jié)合,、與小波相結(jié)合等來(lái)提高壓縮比，從而改善解碼圖像的質(zhì)量,。本文在圖像解碼完成的基礎(chǔ)上,，利用雙線(xiàn)性與最近鄰插值相融合的方法對(duì)圖像進(jìn)行解碼后處理，使方塊效應(yīng)得到緩解,，更好地改善了圖像的質(zhì)量,。
1 分形圖像編解碼的原理
　 分形圖像編碼以迭代函數(shù)系統(tǒng)和拼貼定理為理論基礎(chǔ)，利用圖像的自相似性,達(dá)到壓縮圖像的目的,。JACQUIN A E將迭代函數(shù)系統(tǒng)的子映射定義域限制在圖像的一個(gè)字塊上(局部迭代函數(shù)系統(tǒng)LIFS)[3-4],，提出了基于分塊的圖像壓縮編碼系統(tǒng)。
1.1 傳統(tǒng)分形圖像編碼過(guò)程
　 分形編碼一般分為圖像分割,、搜索匹配和參數(shù)量化三步進(jìn)行,。
　 首先,將原圖分割成互不重疊的n個(gè)值域塊Ri，大小為M×M,，覆蓋整個(gè)圖像,。同時(shí),將原圖按一定步長(zhǎng)分割為尺寸較大的可互相重疊的定義域塊Di，一般取值域塊的2倍邊長(zhǎng),，即大小為2M×2M,。每個(gè)Di經(jīng)四鄰域像素值平均得到M×M的定義域塊，再通過(guò)8個(gè)基本仿射變換擴(kuò)大為8個(gè)子塊,這種子塊的全體就構(gòu)成了碼本,，即搜索空間[5],。
    然后，對(duì)于值域塊里給定的Ri,，通過(guò)最小均方誤差（MSE）原則在碼表的定義域塊Di的搜索空間中尋找與之最匹配的Di以及壓縮映射Wi[5],使式(1)成立：
    
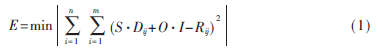
其中,Dij是定義域塊經(jīng)過(guò)旋轉(zhuǎn)反射和伸縮變換后的像素值,，Rij是值域塊的像素值,I為灰度值為1的數(shù)據(jù)塊。
    當(dāng)式(1)中E取最小時(shí)可得到最佳對(duì)比度S和灰度偏移量O:
  
    綜上所述,，分形編解碼的主要任務(wù)是為每一值域塊在碼本中尋找最佳匹配的定義域塊,，它的分形碼文件記錄的是圖像中與值域塊匹配的定域塊位置、最佳對(duì)比度,、灰度偏移量和基本變換的方式,。從中反映的只是圖像中各個(gè)子圖之間的相互關(guān)系,，與值域塊以及定義域塊的大小無(wú)關(guān),。由此發(fā)現(xiàn),分形編碼有一個(gè)與其他編碼方法不同的特性——分辨率無(wú)關(guān)性。
2 利用分辨率無(wú)關(guān)性解決高壓縮比下的方塊效應(yīng)
2.1 塊狀效應(yīng)的產(chǎn)生
    分形圖像編碼中的塊狀效應(yīng)主要是由兩方面因素造成的。
    (1)由于在分形壓縮編碼中采用的是互不交疊的圖像塊分割方法,，各個(gè)圖像塊獨(dú)立地進(jìn)行編碼,，隔離了塊與塊之間的關(guān)系。而且算法采用塊平均的均方誤差準(zhǔn)則尋找最佳匹配塊,，造成圖像塊邊界的匹配誤差與整個(gè)塊的匹配誤差存在較大差異[6],，從而導(dǎo)致解碼后的塊與相鄰塊的邊界部分產(chǎn)生不連續(xù)，造成了視覺(jué)上的塊狀效應(yīng),。
    (2)為了降低分形編碼的復(fù)雜度和提高壓縮比,，各種不同的塊分類(lèi)方法被應(yīng)用于分形壓縮。然而,塊的重建只是用它的灰度均值來(lái)恢復(fù)塊中的每一像素點(diǎn)的灰度,，加快了以塊為單位的灰度變化,，原本細(xì)微的灰度變化被忽略，在圖像的邊界產(chǎn)生不連續(xù),，形成邊緣,。
    因此，去除塊狀效應(yīng)的基本原則就是平滑塊間的人工不連續(xù)和保持原圖像的邊緣細(xì)節(jié),。    
2.2 基于分辨率無(wú)關(guān)性的解決方案
    本文基于分形編解碼的分辨率無(wú)關(guān)性,，結(jié)合分辨率越小方塊效應(yīng)越不易察覺(jué)的實(shí)驗(yàn)論證結(jié)果，在對(duì)編碼算法不作任何改動(dòng)的前提下,，提出了一種新的方法,。其基本思路是：先將圖像解碼至低分辨率下，再利用雙線(xiàn)性插值和最近鄰點(diǎn)插值法相融合的算法將圖像還原至同分辨率下,。該算法的優(yōu)點(diǎn)在于:考慮插值點(diǎn)與鄰點(diǎn)之間距離關(guān)系的同時(shí)又考慮到鄰點(diǎn)像素的灰度值分布,，以最近鄰點(diǎn)插值法高通濾波保護(hù)邊緣的特性來(lái)彌補(bǔ)雙線(xiàn)性插值法高頻邊緣細(xì)節(jié)成分丟失的不足[7]，從而有效地消除高壓縮比下的方塊效應(yīng),。
    設(shè)初始低分辨率下圖像為A,，還原所得圖像為B。具體做法如下：
    (1)如果B中(X,Y)的點(diǎn)通過(guò)計(jì)算映射到A中的整數(shù)(x,y),，則點(diǎn)(X,Y)就取該點(diǎn)(x,y)的灰度值,。通過(guò)式(5)將A變換成B：
  
    圖1(a)為原始圖像，圖1(b)為分形解碼圖像,，圖1(c)為本文算法運(yùn)用到圖1(b)上的結(jié)果,。從圖中可看出，經(jīng)過(guò)本文算法處理后,塊效應(yīng)得到一定程度上的消除,，圖像的視覺(jué)質(zhì)量也有極大的改善,。
    本文采用雙線(xiàn)性插值法與最近鄰點(diǎn)插值法相融合的方法，更好地保留了邊緣特性,，明顯改善了分形壓縮在圖像恢復(fù)時(shí)帶來(lái)的方塊效應(yīng),提高了解碼圖像的質(zhì)量,。實(shí)驗(yàn)證明,該方法達(dá)到了預(yù)期的效果,，實(shí)驗(yàn)結(jié)果良好。
參考文獻(xiàn)
[1] 婁莉,劉天時(shí).一種基于分形的圖像編碼改進(jìn)算法[J].微計(jì)算機(jī)信息,， 2010,26（4）:206-208.
[2] 黃曉莉.快速分形圖像編碼算法的研究[D].西安：西安科技大學(xué),，2009.
[3] JACQUIN A E. Image coding based on a fractal theory of  iterated contractive image transformations[C]. IEEE Transactions on Image Processing, 1992,IP-1(1):18-30.
[4] BARNSLEY M F,HURD L P. Fractal image compression[M]. Massachusets Wellesley Publishers Inc, 1993.
[5] 宋憑，劉波,曹劍中,等.提升小波與分形相結(jié)合的圖像壓縮[J].光子學(xué)報(bào),，2006,35(11):1785-1787.
[6] 狄紅衛(wèi),，余英林.一種消除分形圖像編碼中塊狀效應(yīng)的算法[J].計(jì)算機(jī)科學(xué), 1999(26):57-58.
[7] 楊紹國(guó)，尹忠科,，羅炳偉.分形插值和分形圖像編碼相結(jié)合進(jìn)行圖像數(shù)據(jù)壓縮[J]. 電子科學(xué)學(xué)刊, 1998,，20(5):699-701.