摘 要: 通過主成分分析并結(jié)合SPSS軟件得到具有高信息含量的A第一主成分和A第二主成分,并分別確定A第一主成分和A第二主成分的函數(shù)解析式。在變量基礎(chǔ)上增加A第一主成分變量,并再次通過主成分分析得到具有高信息含量的B第一主成分和B第二主成分,并分別確定B第一主成分、B第二主成分和綜合主成分的函數(shù)解析式,對(duì)三者分別進(jìn)行排序,確定患病與健康的判定指標(biāo)。
關(guān)鍵詞: 主成分分析;多因子綜合分析;統(tǒng)計(jì)回歸分析;SPSS技術(shù)
主成分分析是將多個(gè)變量通過線性變換以選出較少個(gè)數(shù)重要變量的一種多元統(tǒng)計(jì)分析方法。在實(shí)際課題中,為了全面分析問題,往往提出很多與此有關(guān)的變量,因?yàn)槊總€(gè)變量都在不同程度上反映這個(gè)課題的某些信息。但是,在用統(tǒng)計(jì)分析方法研究多變量的課題時(shí),變量個(gè)數(shù)太多就會(huì)增加課題的復(fù)雜性。人們希望變量個(gè)數(shù)較少,同時(shí)得到較多的信息。變量之間存在一定的相關(guān)關(guān)系,當(dāng)2個(gè)變量之間有一定相關(guān)關(guān)系時(shí),可以解釋為這2個(gè)變量反映此課題的信息有些重疊。主成分分析是對(duì)原先提出的所有變量建立盡可能少的新變量,這些新變量在反映課題的信息方面盡可能保持原有的信息[1]。
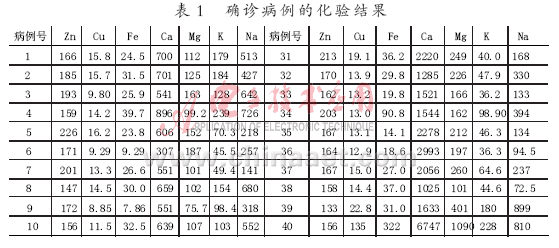
人們到醫(yī)院就診時(shí),通常要化驗(yàn)指標(biāo)來協(xié)助醫(yī)生的診斷。診斷就診人員是否患腎炎時(shí)通常要化驗(yàn)人體內(nèi)各種元素含量,主要包括鋅(Zn)、銅(Cu)、鐵(Fe)、鈣(Ca)、鎂(Mg)、鉀(K)及鈉(Na)。表1是確診病例的化驗(yàn)結(jié)果,其中1~30號(hào)病例是已經(jīng)確診為腎炎病人的化驗(yàn)結(jié)果,31~60號(hào)病例是已經(jīng)確定為健康人的結(jié)果[2]。在論文中列出的數(shù)據(jù)是原始數(shù)據(jù)中1~10號(hào)病例及31~40號(hào)病例的數(shù)據(jù),運(yùn)用主成分計(jì)算時(shí)以所有數(shù)據(jù)為初始數(shù)據(jù)。
1 主成分分析模型

2 模型應(yīng)用
2.1 問題分析解決


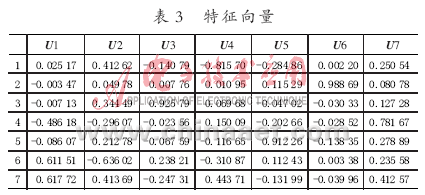
因C1=[X1 X2 … X7]*[U11 U12 … U17]T,因?yàn)樘卣髦档姆讲钬暙I(xiàn)率為72.67 %,表明C1包含原變量中的絕大部分信息,則在原來7個(gè)因子的基礎(chǔ)上引入C1作為第8個(gè)因子,C1=[0.70502、0.6341、0.87415、0.80724、0.4212、0.62897、0.37992、0.85489、0.57495、0.71527、-0.74635、0.03003、-0.30047、-0.03826、-0.80605、-1.32826、-0.5588、-0.00363、0.37216、-3.19199]。再將其做標(biāo)準(zhǔn)化變化,再次通過主成分分析并結(jié)合SPSS軟件確定B第一主成分F1、第二主成分F2和綜合主成分F。根據(jù)對(duì)這8個(gè)因子通過SPSS的因子分析如表4、表5所示。

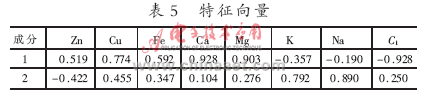
由表5可知C1與5種元素有著顯著的相關(guān)性[5],可見許多變量之間直接的相關(guān)性比較強(qiáng),證明它們存在信息上的重疊。
2.2 主成分表達(dá)式
主成分個(gè)數(shù)提取原則為主成分對(duì)應(yīng)特征值>1的前m個(gè)主成分。特征值在某種程度上可以被看成是表示主成分影響力度大小的指標(biāo),如果特征值<1,說明該主成分的解釋力度還不如直接引入原變量的平均解釋力度,因此一般可以用特征值>1作為納入標(biāo)準(zhǔn)。通過表4可知,提取2個(gè)主成分,即m=2。從表5可知C1、Zn、Cu、Fe、Ca、Mg在B第一主成分上有較高的載荷,說明B第一主成分基本反映了這些指標(biāo)的信息,K、Na在B第二主成分上有較高的載荷,說明B第二主成分基本反映了K、Na 2個(gè)指標(biāo)的信息。所以提取2個(gè)主成分是基本反映全部指標(biāo)的信息,所以決定用2個(gè)新的變量來代替原來的8個(gè)變量。通過SPSS將表5中的數(shù)據(jù)除以主成分相對(duì)應(yīng)的特征值開平方根,得到兩主成分中每個(gè)指標(biāo)所對(duì)應(yīng)的系數(shù)。將得到的特征向量與標(biāo)準(zhǔn)化后的數(shù)據(jù)相乘,然后就可以得到主成分表達(dá)式[6]:

![]()
由(1)、(2)、(3)式得到B第一主成分F1、B第二主成分F2和綜合主成分F的數(shù)據(jù)及排名,如表6所示。
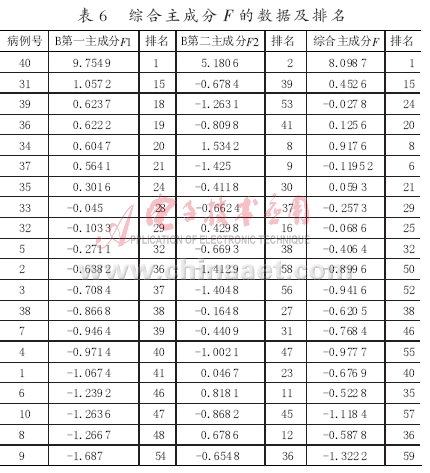
由表6可以看出第一主成分中以0為臨界值,0.1為修正值,即(-0.1,0.1)為不穩(wěn)定狀態(tài),此狀態(tài)下的就診人員將隨機(jī)被確定為患者和健康者中的1個(gè)。而當(dāng)F1>0.1時(shí),將此時(shí)對(duì)應(yīng)的就診人員確定為健康者;當(dāng)F1<-0.1時(shí),將此時(shí)的就診人員確定為患者。經(jīng)此方法判定的患者與健康者與表1中的患者與健康者基本一致,并且與用綜合主成分分析得到的結(jié)果基本一致。其判定的準(zhǔn)確性可以達(dá)到95%以上,因此具備很強(qiáng)的可信性與科學(xué)性。
本文創(chuàng)新點(diǎn)在于模型中連續(xù)做了2次主成分分析,即二次主成分分析,并伴有大量的數(shù)據(jù)處理和數(shù)據(jù)分析,合理的結(jié)論背后擁有強(qiáng)大的理論支持和數(shù)據(jù)支持,具有很強(qiáng)的科學(xué)性和可信性。不過,確診病人還是需要通過醫(yī)生的具體分析,以達(dá)到所需效果。
參考文獻(xiàn)
[1] 主成分分析[EB/OL].http://baike.baidu.com/view/45376.htm,2009-03.
[2] 北京工業(yè)大學(xué)數(shù)學(xué)建模競賽初賽試題B題[EB/OL].http://www.wendang.com/soft/16922.htm,2008-05.
[3] 主成分分析[EB/OL].http://ec.njue.edu.cn/tjx/wf_dytjfx/slides/chap03.2009-05.
[4] 張文霖.主成分分析在SPSS中的操作和應(yīng)用[J].理論與分析,2005(12):31-35.
[5] 王林輝.基于主成分分析的棉花品種綜合評(píng)價(jià)及聚類分析[J].廣東農(nóng)業(yè)科學(xué),2009(1):29-32.
[6] 董寒青.解析SPSS對(duì)主成分分析的計(jì)算技術(shù)[J].知識(shí)叢林,2004(3):117-118.

