摘 要: FCM算法作為基于目標函數(shù)的模糊聚類算法中最經(jīng)典的算法之一,,在實際應用中得到了深入的研究,,但FCM算法需要人為給定分類數(shù)C,因此破壞了聚類的無監(jiān)督性,。針對FCM算法的不足,,提出了利用密度指標確定初始聚類數(shù)目上限Cmax,并且對有效性指標進行了改進,,計算對于(1,,Cmax]中的每一個c對應的有效性函數(shù)值,根據(jù)有效性評判,,確定最佳聚類數(shù),,實現(xiàn)了自動得到最佳分類數(shù)的算法。
關(guān)鍵詞: 模糊C-均值,;模糊聚類,;密度函數(shù);有效性指標
模糊C-均值(FCM)聚類算法是聚類分析中最重要的聚類算法之一,,在特征分析,、模式識別、圖像處理,、分類器設(shè)計等技術(shù)中應用非常廣泛[1],。
但FCM算法存在著以下幾點不足[1]:(1)算法的性能依賴于初始聚類中心和初始隸屬度函數(shù)的選取;(2)事先必須確定聚類的個數(shù);(3)模糊指標的選擇;(4)收斂到局部極值問題。
很多學者針對這些問題進行了研究,。如參考文獻[2]采用貪心算法選取有代表性的點作為初始中心,提出一種基于權(quán)重的初始中心點選取算法, 得出了優(yōu)化聚類初始中心的模糊C-均值方法,;參考文獻[5]通過加入點密度加權(quán)系數(shù)和特征矢量權(quán)重, 提出一種具有兩階段的模糊FCM聚類改進算法。
本文針對FCM算法事先必須確定聚類個數(shù)這一不足,,提出了兩點改進思路: (1)在初始聚類中心的選擇上提出了一種密度指標方法,,利用該方法可以在全局范圍內(nèi)選取初始值,降低了算法受初始值影響易陷入局部最優(yōu)的可能性,,從而得到最大聚類個數(shù),;(2)提出了有效性指標的改進算法,從而更加客觀公正地評判聚類結(jié)果有效性,。
1 聚類數(shù)c和初始聚類中心的確定
1.1 密度指標
密度指標的方法對聚類中心的選擇有重要意義,,該方法的基本規(guī)則是,保證成為聚類中心的數(shù)據(jù)點周圍的數(shù)據(jù)點密度大于事先設(shè)定的臨界值,。它從全局出發(fā),,對每個數(shù)據(jù)點平等相待,,認為每個數(shù)據(jù)點都有可能成為聚類中心,并根據(jù)每個數(shù)據(jù)點周邊的數(shù)據(jù)密度計算該數(shù)據(jù)點是否有可能成為聚類中心,,甚至計算成為聚類中心的可能性的大小,。這樣,可以保證各個聚類中心點周邊數(shù)據(jù)點密度最高,使得算法不會因為初始值影響而陷入局部最優(yōu),。



2 自適應最佳FCM聚類個數(shù)確定算法
在確定最佳聚類數(shù)時,需要對從1~n的所有c值進行循環(huán)運算,,而每一個c值在運算過程中都會產(chǎn)生聚類中心,,這樣聚類中心的數(shù)量就會隨著樣本數(shù)目的增加而急劇增加,致使算法的時空復雜度很大,。本論文將利用密度指標確定初始聚類數(shù)目上限Cmax,,確定初始聚類數(shù)目上限后,就可以減少循環(huán)運行次數(shù),,從而相應地減少初始化聚類中心的數(shù)目,大大提升算法的時空效率,。
因為聚類過程沒有預先定義數(shù)據(jù)集中哪一種期望的關(guān)系是有效的,所以它是一種無監(jiān)督的學習方法,,因此很多聚類算法依靠假設(shè)和猜測進行有效性的判斷,,為解決此問題,多數(shù)學者提出了聚類有效性指標方法,,它被認為是評判聚類結(jié)果有效性的一種客觀公正的質(zhì)量評價方法,。本論文將利用改進的有效性指標計算對于(1,Cmax]中的每一個c對應的有效性函數(shù)值,,根據(jù)有效性評判,,得到最佳聚類數(shù)Copt。
算法的描述如下:
輸入:待聚類分析的數(shù)據(jù)集合Dset.txt,,最大迭代次數(shù)Rmax,。
輸出:最佳聚類數(shù)Copt、迭代次數(shù)l和目標函數(shù)值obj,。
算法:

3 實驗分析
實驗數(shù)據(jù):IRIS數(shù)據(jù),;
數(shù)據(jù)特征:分為三種類型,每種類型中包括50個四維的向量,。
實驗步驟:
(1)先按照傳統(tǒng)FCM算法對數(shù)據(jù)集聚類,,此時需預先給出聚類數(shù)c為3,并在集合中隨機選出3個初始中心,,得到算法目標函數(shù)的變化曲線如圖1所示,。
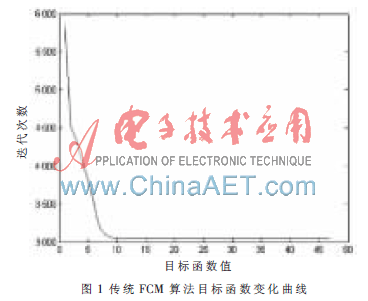
(2)根據(jù)密度指標函數(shù)Dsty(data),得出初始聚類數(shù)目Cmax=8,,并根據(jù)Ics( )得到8個初始聚類中心,。
(3)根據(jù)有效性指標和類合并的方法步驟,,給出相似度計算條件?著1=0.4,?著2=0.8,,經(jīng)過循環(huán)計算得到最終的聚類結(jié)果,,Copt=3,目標函數(shù)變化曲線如圖2,。
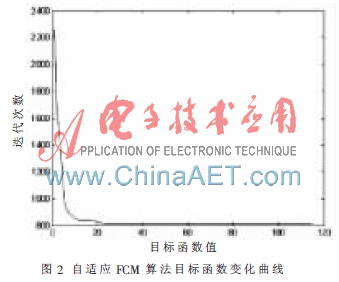
通過實驗可以看出改進后的FCM 算法根據(jù)密度指標函數(shù)自適應地得到最大聚類數(shù)Cmax和聚類中心,,再根據(jù)有效性指標和類的合并方法得到最優(yōu)的聚類數(shù)Copt和聚類中心,而后用 FCM 算法計算得到的結(jié)果屬于有效聚類,,能更準確地對數(shù)據(jù)集進行劃分,,且通過對比目標函數(shù)的變化曲線,可以看出改進后的算法由于是在全局范圍內(nèi)選擇初始值,目標函數(shù)相對于傳統(tǒng)FCM算法更容易收斂到全局最優(yōu),降低了算法對初始中心的依賴,。因此本論文提出的自適應模糊C-均值算法是有效的,。
由于實驗中選取的數(shù)據(jù)集屬于特定類型的數(shù)據(jù),按照改進后的算法得到的結(jié)果更合理也更準確,,尚未觀察出聚類結(jié)果存在的不合理性,,但是當數(shù)據(jù)集合不是IRIS類型的數(shù)據(jù)時,很可能得不到理想的聚類效果,,本論文尚未對所有類型的數(shù)據(jù)集做實驗分析,,這將是今后進一步研究的方向。
參考文獻
[1] 江克勤,施培蓓.優(yōu)化初始中心的模糊C-均值(FCM)算法[J].合肥工業(yè)大學學報(自然科學版),2009,32(5):762-
765.
[2] 單凱晶,肖懷鐵.初始聚類中心優(yōu)化選取的核C-均值聚類算法[J].計算機仿真,2009,26(7):118-121.
[3] 齊淼,張化祥.改進的模糊C-均值聚類算法研究[J].計算機工程與應用,2009,,45(20):133-135.
[4] 張國鎖,周創(chuàng)明,雷英杰.改進FCM聚類算法及其在入侵檢測中的應用[J].計算機應用,2009,29(5):1336-1338.
[5] 劉坤朋,羅可.改進的模糊C均值聚類算法[J].計算機工程與應用,2009,45(21):97-99.

