摘 要： 迭代重建法能夠解決徑向采樣數(shù)據(jù)欠采樣后網(wǎng)格化重建存在偽影的問題,。非線性反演法能夠提高并行磁共振成像圖像重建的質(zhì)量，它能夠利用少量k-空間中心的數(shù)據(jù)來同時(shí)估計(jì)圖像的信息和線圈的靈敏度,。利用TV正則化的高斯牛頓迭代方法對(duì)欠采樣因子較大的徑向軌跡并行磁共振數(shù)據(jù)進(jìn)行重建,，得到無偽影的高質(zhì)量圖像。
關(guān)鍵詞： 徑向采樣,；并行成像,；網(wǎng)格化；非線性反演
磁共振成像MRI（Magnetic Resonance Imaging）自1973年由LAUTERBUR P提出并得到第一幅質(zhì)子密度加權(quán)圖像[1]到現(xiàn)在已經(jīng)經(jīng)歷了幾十年的發(fā)展,，但是傳統(tǒng)的MRI成像時(shí)間長(zhǎng),，對(duì)于一些運(yùn)動(dòng)快的部位的成像有偽影。因此,，幾十年來學(xué)者們一直致力于加快MRI成像速度,。傳統(tǒng)MRI采用笛卡爾軌跡，它的重建方法簡(jiǎn)單,，但逐行采集對(duì)運(yùn)動(dòng)造成的偽影很敏感,。非笛卡爾采樣（如徑向采樣）比笛卡爾采樣有明顯的優(yōu)勢(shì)：(1)徑向采樣數(shù)據(jù)的每條線含有等量的低頻到高頻信息，這有利于MRI圖像的欠采樣重建,；（2）徑向采樣模式?jīng)Q定其對(duì)k-空間中心數(shù)據(jù)的過采樣,，而k-空間中心數(shù)據(jù)決定圖像的主要信息，因此徑向采樣對(duì)物體的運(yùn)動(dòng)沒有笛卡爾采樣那么敏感,，這也有利于MRI圖像的對(duì)比度和并行成像,，從欠采樣數(shù)據(jù)中獲得低分辨率圖像。
由于徑向采樣不是均勻采樣,，因此不能直接進(jìn)行傅里葉變換而得到圖像,。目前對(duì)徑向采樣的重建方法主要有非均勻傅里葉變換NUFFT（Non-Uniform FFT）、濾波反投影法FBP（Filtered Back Projection）和網(wǎng)格化法（Gridding）[2-3],。對(duì)于欠采樣數(shù)據(jù),，徑向采樣的重建存在嚴(yán)重的拖尾偽影，BLOCK K T等[4]于2007年提出用合適的懲罰項(xiàng)和TV正則化迭代的方法可以消除拖尾偽影,。近年來有研究顯示,，正則化高斯牛頓迭代法已成功應(yīng)用于并行成像。如今，將非笛卡爾采樣軌跡應(yīng)用到多通道并形成像是研究的熱點(diǎn),。本文將用網(wǎng)格化方法把徑向采樣數(shù)據(jù)插值到網(wǎng)格點(diǎn),，然后利用TV正則化高斯牛頓迭代法對(duì)多通道徑向稀疏采樣數(shù)據(jù)進(jìn)行重建。
1 網(wǎng)格化法
網(wǎng)格化法來源于射電天文學(xué)（Radio Astronomy）,，是插值重建算法的一種,，它的過程是先將非笛卡爾采樣數(shù)據(jù)插值到笛卡爾坐標(biāo)系下均勻分布的網(wǎng)格點(diǎn)上，然后進(jìn)行傅里葉變換得到磁共振圖像,。1985年,，O′SULLIVAN對(duì)網(wǎng)格化法進(jìn)行了研究，認(rèn)為最理想的卷積核函數(shù)是無限長(zhǎng)的sinc函數(shù),，然而實(shí)際過程中只能采用有限長(zhǎng)的卷積核函數(shù),。1991年，美國(guó)Stanford大學(xué)的JACKSON J L提出用Kaiser-Bessel窗函數(shù)作為卷積函數(shù)能夠得到較好的插值結(jié)果,，這一結(jié)論得到廣泛的認(rèn)同,。
2 非線性反演法
對(duì)于并行磁共振成像的圖像重建，基本的信號(hào)方程可以理解為一個(gè)非線性方程,，正則化非線性反演法可以同時(shí)獲得圖像和線圈靈敏度[5-6],。用Fs代表采樣軌跡，從N個(gè)線圈接收到采樣后的數(shù)據(jù)用g表示,，g=(g1,，…，gN)T,，u表示質(zhì)子密度,，未知的線圈靈敏度表示為c=(c1，…,，cN)T,，則信號(hào)方程為：
3 實(shí)驗(yàn)
實(shí)驗(yàn)數(shù)據(jù)來自西門子磁共振儀對(duì)志愿者用徑向脈沖序列進(jìn)行心臟掃描，得到12通道并行徑向數(shù)據(jù),，每個(gè)通道數(shù)據(jù)都是25×256的矩陣,，即采集25條徑向線，每條徑向線采256個(gè)數(shù)據(jù)點(diǎn),。用MATLAB 7.0仿真軟件對(duì)原始數(shù)據(jù)先用網(wǎng)格化方法插值到均勻網(wǎng)格點(diǎn),，繼而用非線性反演法中IRGN法迭代6次，懲則項(xiàng)用2-范數(shù),，正則化用TV法,。
12通道徑向采集數(shù)據(jù)經(jīng)網(wǎng)格化后得到的圖像如圖1所示,，由于只采25條徑向線,，因此各通道圖像都只能重建出心臟的輪廓，而且偽影很嚴(yán)重。
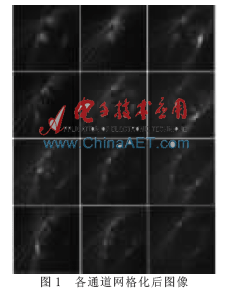
仿真后的圖像如圖2所示,。其中,，圖2（a）為把多通道數(shù)據(jù)直接網(wǎng)格化后對(duì)數(shù)據(jù)用平方和法得到的圖像，從圖像中可以比較清楚地看到心臟,，周圍的偽影是徑向成像獨(dú)有的拖尾偽影,，這是由采集的數(shù)據(jù)過少造成的。圖2（b）為對(duì)網(wǎng)格化后數(shù)據(jù)用IRGN法迭代6次后的圖像,，與圖2（a）相比,，偽影已經(jīng)消失，圖像也清楚很多,。
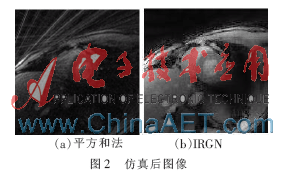
本文結(jié)合多通道并行成像可以加快成像速度和徑向采樣對(duì)低頻數(shù)據(jù)的過采樣的優(yōu)點(diǎn),，同時(shí)又采用IRGN方法消除了徑向稀疏采樣網(wǎng)格化重建存在的拖尾偽影，用非常少的數(shù)據(jù)得到較好的圖像,。
參考文獻(xiàn)
[1] LAUTERBUR P C. Image formation by induced local interactions： examples employing nuclear magnetic resonance [J]. Nature,， 1973， 242： 190-191.
[2] O′SULLIVAN J. A fast sinc gridding algorithm for Fourier inversion in computer tomography[C]. IEEE Transactions on Medical Imaging,， 1985（4）： 200-207.
[3] JACKSON J L,， MEYER C H， MISHIMURADG,， et al. Selection of a convolution function for Fourier inversion using gridding[C]. IEEE Transactions on Medical Imaging,，1991（10）： 473-478.
[4] BLOCK K T， UECKER M,， FRAHM J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint [J]. Magnetic Resonance in Medicine,， 2007（57）： 1086-1098.
[5] KNOLL F， CLASON C,， BREDIES R,， et al. Parallel imaging with nonlinear reconstruction using variational penalties[J]. Magnetic Resonance in Medicine， 2012（67）：34-41.
[6] UECKER M,， HOHAGE T,， BLOCK K T， et al. Image reconstruction by regularized nonlinear inversion-joint estimation of coil sensitivities and image content [J]. Magnetic Resonance in Medicine,， 2008 （60）：674-682.
[7] BAKUSHINSKY A B,， KOKURIN M Y. Iterative methods for approximate solution of inverse problems[M]. Dordrecht： Springer， 2004.
[8] UECKER M,， Zhang Shuo,， FRAHM J. Nonlinear inverse reconstruction for real-time MRI of the human heart using undersampled radial FLASH[J]. Magnetic Resonance in Medicine， 2010（63）：1456-1462.