目前,，軟件方面主要是通過減法算法來實現(xiàn)除法運算，把被除數(shù)作為被減數(shù),，除數(shù)作為減數(shù),，作減法，直到被減數(shù)小于減數(shù)為止,，記錄能夠相減的次數(shù)即得到商的整數(shù)部分,。將所得的余數(shù)乘以10作為被減數(shù)，除數(shù)作為減數(shù),，作減法,，差重新置入被減數(shù)，反復(fù)相減,，直到被減數(shù)小于減數(shù)為止,，記錄能夠相減的次數(shù)即得到商的十分位數(shù)值。依此繼續(xù)下去,，可得到商的百分位數(shù)值,，千分位數(shù)值，……,，要精確到哪一位，就依次做到哪一位,。此方法的缺點是速度慢,，而且最后一位的精度不高，為了克服以上的缺點,，這里設(shè)計一種算法在軟件上改進(jìn)了除法器運算的準(zhǔn)確性和處理速度,。

 

　　1 設(shè)計方法

　　對于任意給定的兩個整數(shù)fenzi和fenmu，設(shè)fenzi為被除數(shù),，fenmu為除數(shù),。為了得到兩個數(shù)相除的十進(jìn)制結(jié)果，本設(shè)計主要通過下面的算法來實現(xiàn),，假如要保留小數(shù)點后面的n位有效數(shù)字,，首先把fenzi乘以10的n次方，賦值給寄存器變量dataO,；接著把fenmu分別乘以10的(n+m),，(n+m一1),，(n+m一2)，…,，1,，O次方分別賦值給(n+m+1)個不同的變量data(n+m+1)，data(n+m),，…,，datal，其中m是fenzi和fenmu的位數(shù)之差(當(dāng)fenzi的位數(shù)多于fenmu時,，m為正,，否則為負(fù))；先求出商的最高位的值,，如果dataO大于data(n+m+1),，則計數(shù)器自動加1，再把dataO和data(n+m+1)的差值賦給data0,，再相減直到data0的值小于data(n+m+1),，此時計數(shù)器的計數(shù)值就是最高位的值；依此用同樣的方法繼續(xù)下去,，就可得到各個位上的值,。對最后一位進(jìn)行四舍五入處理，當(dāng)相減后的dataO<datal時,，再通過比較dataO*2是否大于datal,，如果大于datal，則最后一位計數(shù)器的值加1,，否則不變,，最后把得到的整體值除以10的n次方，也就是小數(shù)點往左移動n位,。傳統(tǒng)除法算法由于采用多次相減的過程來實現(xiàn),，相減的過程耗費了大量時鐘脈沖，而且對運算結(jié)果的最后一位沒有進(jìn)行處理,；而本設(shè)計是通過采用位擴(kuò)展使除數(shù)和被除數(shù)位數(shù)相同,，進(jìn)而對每一位進(jìn)行分開處理，減少了做減法運算的次數(shù),，從而提高運算速度,；同時采用四舍五入的方法對運算結(jié)果進(jìn)行處理，提高準(zhǔn)確性,。上面算法是一種順序方式,，用Verilog硬件描述語言很容易實現(xiàn)，圖1為流程圖,，其中假定fenzi為3位的整數(shù),，fenmu為2位的整數(shù),，除法運算精確到百分位。

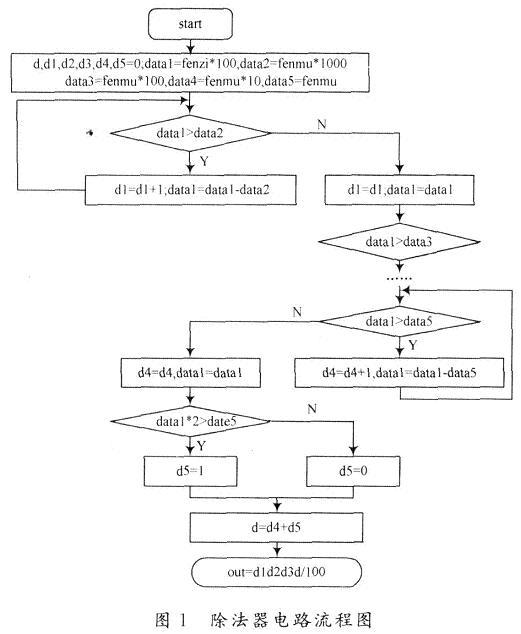
　　2 仿真結(jié)果及分析

　　對上述的流程圖用Verilog描述語言編程,，在Ca—dence的NC—Verilog仿真器下仿真,，設(shè)輸入的Ienzi和fenmu的值分別為128和11，仿真波形如圖2所示,。

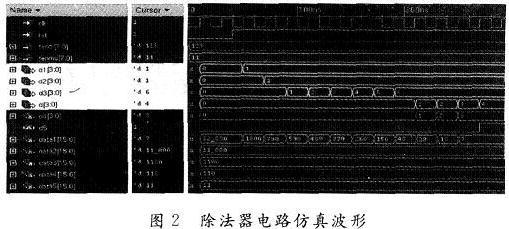
　　從圖2的波形可以看出,，輸出結(jié)果為1 164，除法運算要精確到百分位,，所以往左移動2位,，其最終的值為11．64，而實際的值為11．636 36……,，經(jīng)過四舍五入得到的結(jié)果完成正確,。從仿真時間來看，對于相同的數(shù)值輸入,，本設(shè)計只用了12個脈沖,，而普通除法器至少需要20個脈沖(128／11=11余7，70／11=*,，40／11=3余7,，1l+6+3=20)，相比之下本設(shè)計的除法算法有很大的優(yōu)勢,。

 

　　然而對于兩個位數(shù)相差很大的數(shù)相除,，則本設(shè)計的速度優(yōu)勢更加的明顯，本設(shè)計每一位的運行時間都不會超過9個時鐘脈沖,，因此進(jìn)行,，z位計算的總脈沖也不會超過9n個，而傳統(tǒng)的除法運算需要多個時鐘脈沖,，一般會是本設(shè)計時鐘脈沖的數(shù)倍,。該算法同樣適合小數(shù)的運算，只要把小數(shù)化成整數(shù),，再做同樣的處理，就可以得到精確的結(jié)果,。

 

　　3 結(jié) 語

 

　　通過對除法器算法的改進(jìn),，用四舍五入的方法對數(shù)據(jù)進(jìn)行處理，使得到的結(jié)果準(zhǔn)確性有了進(jìn)一步的提高,；運用移位,、循環(huán)減法，實現(xiàn)數(shù)據(jù)的高速運算,，并能任意設(shè)定計算的精度,。運用此方法在軟件方面設(shè)計除法器對速度和準(zhǔn)確性的提高有積極意義,。