《電子技術應用》
您所在的位置：首頁 > 通信與網(wǎng)絡 > 設計應用 > 基于FastICA的高精度多徑時延估計算法
基于FastICA的高精度多徑時延估計算法
來源：電子技術應用2013年第4期
趙衛(wèi)波， 胡捍英,， 周 游,， 漆 飛
解放軍信息工程大學 信息工程學院, 河南 鄭州450002
摘要： 在高精度無線定位中，針對現(xiàn)有超分辨率時延估計算法在低信噪比時性能較差的問題,，提出了一種基于FastICA的多徑時延估計算法,。利用噪聲子空間對白化矩陣進行修正，并采用參考信號約束初始分離矩陣,，算法可快速收斂至所需的首達徑分量,，最后利用參考信號提取首達徑時延。仿真結果表明,，在信噪比較低的多徑環(huán)境中,，與已有超分辨時延估計算法相比能夠有效提高時延估計精度。
中圖分類號： TN929.5
文獻標識碼： A
文章編號： 0258-7998(2013)04-0079-04
FastICA-based super resolution multipath time delay estimation algorithm
Zhao Weibo, Hu Hanying, Zhou You, Qi Fei
Institute of Information, PLA Information Engineering University, Zhengzhou 450002, China
Abstract： Aming at improving the performance in low SNR environment of super resolution time delay estimation(TDE) in high precision wireless position location, this paper peoposed a multipath TDE algorithm based on FastICA. By modifying the whitening matrix with noise subspace and applying constraint to initial unmixing matrix in FastICA with reference signal, the algorithm reduced the complexity to converge to the expected FAP component. Finally, the time of arrival(TOA) of FAP could be achieved with reference signal. Simulation results showed the improvement on TDE performance compared with current super resolution algorithms in low SNR environment.
Key words : wireless position location; multipath time delay estimation; FastICA; super resolution

    多徑時延估計在無線定位,、雷達和地質勘探等領域有著廣泛應用,，而且在很多應用中期望得到精確的首達徑(FAP)的到達時間(TOA)。相關法[1]是估計信號TOA的經(jīng)典方法,，具有實現(xiàn)簡單,、計算量小的優(yōu)點。但在多徑環(huán)境下,，相關法的時延估計精度受限于系統(tǒng)的采樣率,，其多徑估計性能會進一步降低，并不能滿足高精度定位的需求,。為此,，人們又提出了多種超分辨的時延估計算法以期獲得更加精確的時延。最大似然[2](ML)類的時延估計算法的分辨率可突破系統(tǒng)采樣率的限制,，但其解算需要復雜的多維搜索,，計算量較大。而且，ML估計算法的最優(yōu)性只是對于單徑信號而言,，它并不能有效區(qū)分多徑信號[2],。以多重信號分類[3](MUSIC)算法為代表的子空間類時延估計算法具有良好的多徑分辨能力，估計精度高,，但在信噪比較低時,，MUSIC算法性能下降，對于FAP能量微弱的多徑信號估計會造成一定誤差,。

    獨立分量分析[4]ICA(Independent Component Analysis)是近20年發(fā)展起來的一種信號處理和數(shù)據(jù)分析方法,，ICA通過增大不同信號成分的非高斯性達到分離信號的目的，非高斯性常用峭度和負熵來度量,。而FastICA[5]是一種基于負熵最大化準則的定點快速算法,，它采用擬牛頓迭代算法，以最大化負熵為目標函數(shù),，具有魯棒性好,、收斂速度快、精度高等特點,，在多個領域獲得了較好的應用,。
    接收端信號是由源信號經(jīng)過不同的、相互獨立的路徑延遲信號疊加而成,，本文將獨立成分分析的思想應用到多徑時延估計中,。但傳統(tǒng)FastICA算法[5]在多徑分離時并不能快速獲得FAP分量，需要將所有的路徑分量全部迭代分離后才能確定,，這樣在多徑分布密集的環(huán)境中,，F(xiàn)AP的TOA計算會非常復雜。算法通過對FastICA中白化矩陣的修正和選取特定的初始分離矩陣進行迭代,，可以達到所分離出的信號就是所需FAP分量的目的,。而后根據(jù)所得FAP分量和參考信號即可估計FAP時延。算法充分利用了FastICA算法魯棒性好的特點,，適用于多徑時延估計,，在低信噪比條件下其估計精度相對于其他超分辨時延估計算法明顯改善。
   

    式(7)說明：E(ZZH)是一個對角陣,，符合獨立成分分析的計算條件,。與傳統(tǒng)白化矩陣相比，新的白化矩陣考慮了噪聲對于源信號影響,有助于分離強度較弱的信號分量,。
2.2 利用參考信號約束初始分離矩陣
    傳統(tǒng)FastICA算法中的分離矩陣可以任意初始化,，根據(jù)初始分離矩陣的不同，迭代將隨機收斂至不同的獨立分量,。由于在無線定位中,，期望獲得的是FAP分量,，當多徑分布密集時，通過傳統(tǒng)初始化分離矩陣的方法將所有路徑分量一一分離來確定FAP是不現(xiàn)實的,。本文所提算法通過約束初始分離矩陣,，使算法能夠強制收斂至FAP分量。
    為使FastICA算法能夠應用于非圓復信號的計算,，參考文獻[7]中給出了一種計算負熵的表達式：
    

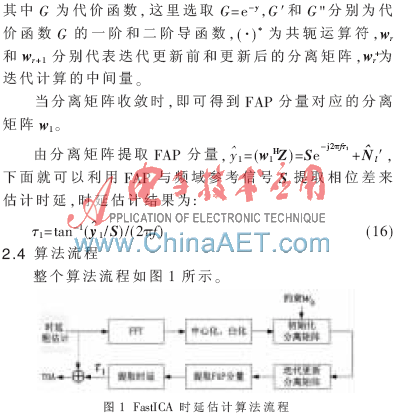
    算法首先根據(jù)時延粗估計的結果選擇一定長度的數(shù)據(jù)做時延精確估計,，最后由FastICA算法得到的精估計結果和粗估計結果就可以得到完整的TOA。
3 仿真結果與分析
　 本文仿真采用傳輸帶寬為10 MHz,、FFT點數(shù)為1 024,、循環(huán)前綴CP長度為72、子載波調制方式為BPSK的OFDM信號,。工作頻率為2 GHz，采樣率為15.36 MHz,。
 仿真1  FastICA算法與其他超分辨時延估計方法精度對比
　 考慮在一個采樣間隔內共有三條路徑的情況,，相對時延分別為：(0.24Ts，-5 dB),、(0.3Ts,，-5 dB)和(0.49Ts，0  dB),，分別仿真最大自然算法ML,、MUSIC算法和FastICA算法的時延估計結果，其中FastICA觀測次數(shù)為15次,，迭代次數(shù)為5次,。圖2給出了1 000次仿真后三種算法的多徑分辨性能。
    圖2比較了FastICA算法與其他算法的多徑分辨性能,。由圖可以看出,，在多徑分布密集、信噪比較低的條件下,，F(xiàn)astICA算法能夠更加準確地估計出FAP時延,。ML算法已經(jīng)不能分辨出采樣間隔內的多條路徑；MUSIC算法也不能完全分辨出所有多徑,，產(chǎn)生了多徑混疊,，F(xiàn)AP時延估計出現(xiàn)了較大誤差；而FastICA算法得益于白化階段的降噪處理可準確分辨相對時延很近的多徑信號,。

    仿真2 FastICA算法在不同信噪比條件下的估計精度
    多徑數(shù)為5,，觀測次數(shù)為15，ICA算法迭代次數(shù)為5次,。分別仿真了在不同信噪比條件下,，ML算法,、MUSIC算法和FastICA算法對FAP的時延估計精度。圖3給出了三種算法在1 000次仿真后的時延估計誤差,其中時延估計誤差用距離誤差來表示,，它等于時延估計的均方誤差乘以光速,。

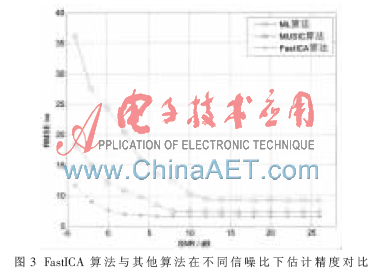
    圖3比較了三種算法的時延估計誤差隨信噪比的變化情況：三種算法的估計誤差都隨著信噪比提高而減小。但在信噪比大于0 dB時,，F(xiàn)astICA算法的誤差對信噪比的變化不敏感,；在信噪比小于0 dB時，三種算法的誤差都有所增大,。但相對于ML和MUSIC算法,，F(xiàn)astICA算法的魯棒性更強，時延估計性能有所提高,。
    仿真3  FastICA算法在不同多徑數(shù)目下的估計性能
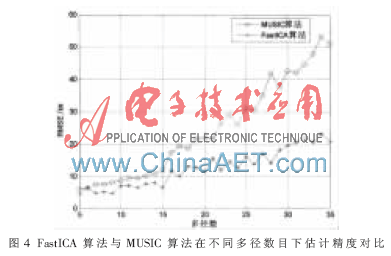
    信噪比SNR為5dB,，觀測次數(shù)為45次，迭代次數(shù)為5次,，分別仿真MUSIC算法和本文所提FastICA算法隨著多徑數(shù)目增加時時延估計性能的變化情況,，圖4給出了1 000次仿真后的結果。
    由圖4可以看出,，隨著多徑數(shù)目的增加,，MUSIC算法和FastICA算法的估計誤差都呈逐漸增大的趨勢。但由于FastICA算法具有較好的多徑分辨能力,，其誤差增長速度明顯小于MUSIC算法,，對多徑數(shù)的敏感度較低。在多徑分布密集的城區(qū)和室內環(huán)境,，算法仍然能夠提供較為理想的時延估計結果,。

　 FastICA算法在時延估計精度上相對于其他超分辨方法有一定提高，但與MUSIC算法類似,，它在白化階段也需要對源信號做特征值分解來估計多徑的數(shù)量,。另外，當信噪比較低時,，算法為了約束初始化分離矩陣需要增大數(shù)據(jù)觀測次數(shù),。這在一定程度上增加了算法的計算量。
    本文提出一種基于FastICA的多徑時延估計算法,，通過修正白化矩陣和利用參考信號初始化分離矩陣,，算法在多徑時延估計中有較高實用性。與其他超分辨時延估計算法相比,，該算法在低信噪比時的估計性能有較大改善,。對信噪比和多徑數(shù)的敏感度較低，魯棒性較強,。在多徑環(huán)境復雜的定位應用中,，本文算法能夠提供較高的估計精度,。
參考文獻
[1] FOCK G,BALTERSEE J, RITTICH S P, et al. Channel  tracking for rake receivers in closely spaced multipath environments[J]. IEEE J. Sel. Area. Comm, 2001(19):2420-2431.
[2] BHARDWAJ T P. Maximum likelihood estimation of time  delays in multipath acoustic channel[C]. Signal Processing  and Communication Systems, ICSPCS, 2008:1007-1011.
[3] Li Xinrong, SUPER-RESOLUTION K P. TOA estimation with diversity for indoor geolocation[J]. IEEE Transactions on Wireless Communications, 2004,3(1):224-234.
[4] NOVEY M, ADALI T. Complex ICA by negentropy maxi-mization[J]. IEEE Transactions Neural Netw.,2008,19(4): 596-609.
[5] TICHAVSKY P Z, KOLDOVSKY P, OJA E. Performance  analysis of the fastica algorithm and Cramér-Rao bounds  for linear independent component analysis[J]. IEEE Transactions on Signal Process, 2006(54):1189-1203.
[6] ALSINDI N, LI X, PAHLAVAN K. Analysis of TOA estimation using wideband measurements of indoor radio propagations[J]. IEEE Trans. Instrum.Meas., 2007,56(5):1537-1545.
[7] NOVEY M,ADALI T.Extending the complex FastICA algorithm to noncircular sources[J].IEEE Trans.Signal Process., 2008,56(5):2148-2154.
[8] ADALI T, NOVEY M, CARDOSO J F. Complex ICA using nonlinear functions[J]. IEEE Transactions on Signal Process,2008,56(9):4536-4544.    (收稿日期：2012-08-31)

此內容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權禁止轉載,。