《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 嵌入式技術(shù) > 設(shè)計應(yīng)用 > 基于均勻圓陣的互耦誤差校正算法研究
基于均勻圓陣的互耦誤差校正算法研究
來源：電子技術(shù)應(yīng)用2013年第5期
魯祖坤,， 高 鷹,， 石 宇,， 劉 揚(yáng)
空軍航空大學(xué) 信息對抗系,，吉林 長春130022
摘要： 陣元之間的互耦效應(yīng)嚴(yán)重影響了DOA的估計性能,?；诰鶆驁A陣,，提出了一種互耦條件下的波達(dá)方向估計和互耦誤差自校正算法,。利用帶狀循環(huán)矩陣的特性對均勻圓陣的互耦誤差建立數(shù)學(xué)模型,，再利用MUSIC算法和迭代法對互耦誤差矩陣和波達(dá)方向同時進(jìn)行估計,，自校正方法無需任何輔助陣元即可實(shí)現(xiàn)兩類參數(shù)的估計。仿真實(shí)驗(yàn)表明,，算法很好地解決了均勻圓陣的互耦問題,，能夠比較準(zhǔn)確地估計出波達(dá)方向角和互耦誤差值。
中圖分類號： TN911.23
文獻(xiàn)標(biāo)識碼： A
文章編號： 0258-7998(2013)05-0107-04
Mutual coupling error correction algorithm based on the uniform circular array
Lu Zukun,， Gao Ying,， Shi Yu， Liu Yang
Department of Information Countermeasure, Aviation University of Air Force, Changchun 130022, China
Abstract： Mutual coupling effect had a serious impact on the performance of DOA estimation between the array elements. Based on the uniform circular array, a DOA estimation and mutual coupling error self-correction algorithm was proposed under the condition of mutual coupling effect. The mathematical model of mutual coupling error was built which used the banded circulant matrix. Then, the mutual coupling matrix and DOA was estimated which used the MUSIC algorithm and iterative methods at the same time. Self-correction method did not require any auxiliary array element , and can implement two types of parameters estimates. Simulation result shows that the algorithm has a good solution to the problem of uniform circular array mutual coupling, and can estimate the DOA and mutual coupling error accurately.
Key words : uniform circular array,；mutual coupling error,；DOA estimation； multiple signal classification(MUSIC),；array signal processing

    波達(dá)方向估計廣泛應(yīng)用于雷達(dá),、聲納、移動通信等多個領(lǐng)域,。目前波達(dá)方向估計技術(shù)已應(yīng)用到衛(wèi)星和飛機(jī)上,。由于衛(wèi)星和飛機(jī)體積的限制，一般衛(wèi)星和飛機(jī)基站上陣元之間的距離都比較小,，而對于陣元間距比較小的陣列,，陣元之間的互耦效應(yīng)不容忽視,，互耦問題是一個重要的研究方向[1]。解決互耦問題的方法一般是先測量互耦系數(shù),，再通過測量值對波達(dá)方向估計算法進(jìn)行修正[2],。但是測量的精度往往不能滿足實(shí)際工程應(yīng)用的需要,當(dāng)用帶誤差的測量值對互耦效應(yīng)進(jìn)行補(bǔ)償時，會使波達(dá)方向估計算法的性能更加惡化,。本文利用帶狀循環(huán)矩陣的特性對均勻圓陣的互耦誤差矩陣建立數(shù)學(xué)模型,，再用MUSIC算法和迭代法對互耦誤差矩陣和波達(dá)方向進(jìn)行同時估計，不需要任何輔助陣元,，實(shí)現(xiàn)比較簡單,，為波達(dá)方向估計算法的實(shí)際工程應(yīng)用提供有益參考。


  

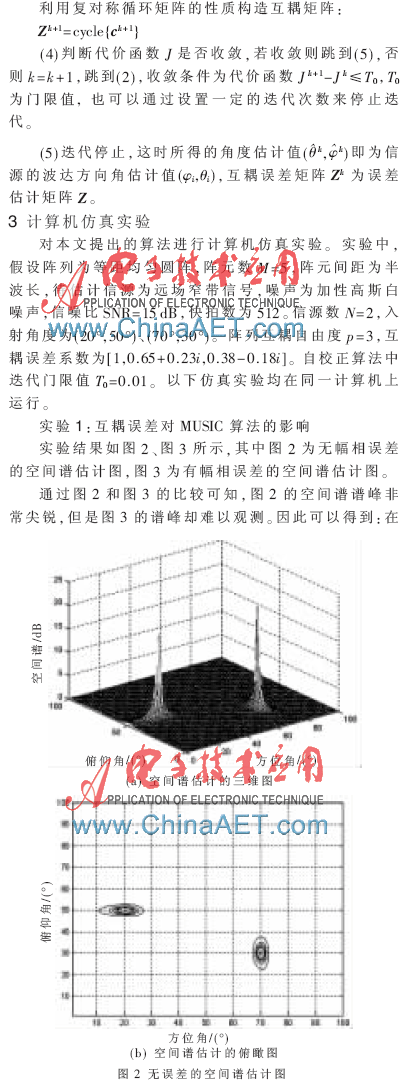
沒有互耦誤差的情況下,，MUSIC算法能夠很好地估計出信源的波達(dá)方向,，但是當(dāng)存在互耦誤差時，MUSIC算法的估計性能急劇下降,，嚴(yán)重影響了波達(dá)方向的估計性能,。
    實(shí)驗(yàn)2：自校正算法對互耦誤差的校正
    實(shí)驗(yàn)結(jié)果如圖4和表1所示。圖4為本文算法對互耦校正后的空間譜估計圖,，表1為互耦誤差真實(shí)值與估計值的對照表,。

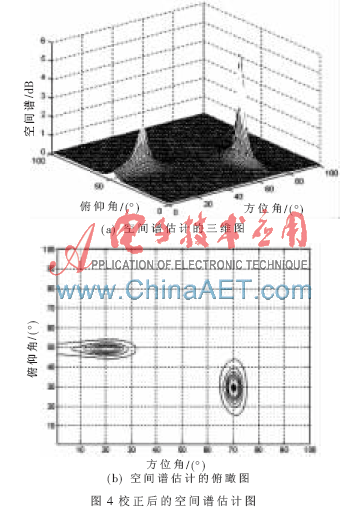
    與圖3相比，圖4的空間譜譜峰很明顯,，因此本文的自校正算法能夠很好地估計信源的波達(dá)方向角,。表1驗(yàn)證了本文算法能夠很好地估計出陣元之間的互耦誤差值，并且互耦誤差的真實(shí)值與估計值之間的誤差在0.01的范圍內(nèi),。
    本文針對均勻圓陣的特殊結(jié)構(gòu)，先對陣列結(jié)構(gòu)進(jìn)行了詳細(xì)的分析,，建立了基于均勻圓陣的導(dǎo)向矢量矩陣,，利用帶狀循環(huán)矩陣的特性對互耦誤差矩陣建立了數(shù)學(xué)模型，并結(jié)合子空間原理和MUSIC算法,，提出了一種基于均勻圓陣的互耦誤差自校正及DOA估計算法,，該方法對互耦矩陣和DOA同時進(jìn)行估計，很好地解決了均勻圓陣的互耦問題,。仿真結(jié)果證明了本文提出算法的有效性,。本文提出的算法對于解決波達(dá)方向估計的實(shí)際工程應(yīng)用具有重要意義。
參考文獻(xiàn)
[1] 閔永生,，羅景青,，吳世龍.基于均勻圓陣的方位估計及互耦自校正算法[J].探測與控制學(xué)報，2011,，33(6)：66-70.
[2] 王布宏,，王永良,，陳輝，等.均勻線陣互耦條件下的魯棒DOA估計及互耦自校正[J].中國科學(xué) E輯：科學(xué)技術(shù),，2004,，34(2)：229-240.
[3] Lin Min，Yang Luxi. Blind calibration and DOA estimation with uniform circular arrays in the presence of mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters,，2006(5)：315-318.
[4] ZHANG T T,，LU Y L HUI H T.Compensation for the mutual coupling effect in uniform circular arrays for 2D DOA  estimations employing the maximum likelihood technique[J]. IEEE Trans.on Aerospace and Electronic Systems，2008,，44(3)：1215-1221.
[5] Ye Zhongfu,， Dai Jisheng，Xu Xu. DOA estimation for uniform linear array with mutual coupling.IEEE Trans[J].on  Aerospace and Electronic Systems,2009,，45(1)：280-288.
[6] Sun Xuebin,， Zhou Zheng.A tracking-based target location  algorithm in wireless sensor networks[J]. The Journal of China Universities of Posts and Telecommunications，2004,，11(1)：17-23.
[7] 姚林宏,，高鷹，石宇,，等.基于均勻線陣的改進(jìn)MUSIC算法[J].吉林大學(xué)學(xué)報（信息科學(xué)版）,，2010，28(6)：558-562.
[8] 王陽,，高鷹,，姜宏，等.多徑效應(yīng)下MIMO雷達(dá)的DOA估計算法[J]. 四川兵工學(xué)報,，2011,，32(12)：14-17.
[9] 王永良，陳輝,，彭應(yīng)寧,，等.空間譜估計理論與算法[M].北京：清華大學(xué)出版社，2004.
[10] 張賢達(dá).現(xiàn)代信號處理[M].北京：清華大學(xué)出版社,，2002.
[11] 王鼎,，李長勝，吳瑛.兩均勻陣列在互耦影響下MUSIC算法的性能分析[J].雷達(dá)科學(xué)與技術(shù),，2010,，8(2)：163-170.

此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。